背包问题（DP）

回顾

再来回顾一下背包问题，背包问题是一个典型的组合问题，目标是让我们在容量为 W 的背包中尽可能装价值越高的物品，其中每件物品都对应自己的重量 w_i 和价值 v_i 。前面我们通过暴力求解的方式将所有可能的组合一一列举出来，然后找到价值最高的组合。但是这样做的效率非常低，时间复杂度达到了指数级的 Θ(2ⁿ) ，因此它不能成为一种我们可以接受的算法。

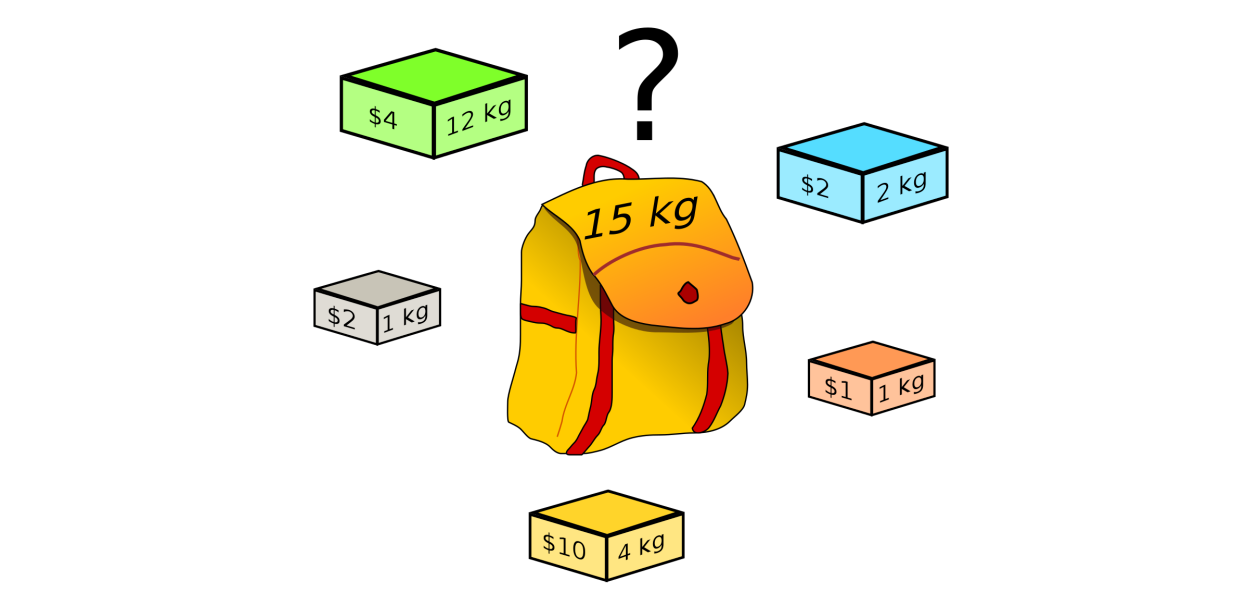
如用动态规划来解决背包问题，事情就会变得简单得多。这里我们用两种方式来实现：自底向上（bottom-up）和自顶向下（top-down）。两者的区别可以这样来理解，假设我们需要用一些零件来拼接一件工艺品，自底向上就好比一名技术精湛的工人，虽然他不知道最后这些零件要拼出一件什么东西，但他深知这些零件的构造，熟悉拼接过程中的顺序，因此如果他一直重复拼接的过程就能最终拼出一件工艺品，因此自底向上用到的最多的方法是迭代；而自顶向下则好似一名工程师，他有一张该工艺品的设计图纸，懂得每一部分的具体功能，并且细分至零件，最后根据这张图纸将它们拼接起来，因此自底向上用到的最多的方法是递归。有同学就会问了，这和分治有什么区别？答案是当然有，工程师很聪明，因为他从来没有接触过零件的组装，因此每当有一部分零件组装好了之后，它都会拿笔记录下来组装的过程，下次组装相同的零件的时候就会大大缩短所需要的时间。下面我们就来看看这两种方式是如何在背包问题中实现的吧！

自底向上

我们先来考虑一下背包问题的子问题。假设物品数为 n，背包容量为 W。子问题可以首先分为如何挑选这些物品，使得组合的价值最大，同时保证总重量小于等于 x，其中 1 ≤ x ≤ W；当然，在挑选物品时，我们也可以只考虑前 i 个物品（1 ≤ i ≤ n），因此，子问题可以被进一步细分为如何挑选前 i 个物品，使得组合的价值最大，同时保证总重量小于等于 x。

再来说说子问题之间的关系，我们用 S(i, x) 来表示任意一个子问题，对于第 i 个物品，我们有两种可能，选或不选。如果不选，我们就从前 i - 1 件物品中找最大的组合，总重量不超过 x。如果选了，那么还是从前 i - 1 件物品中找最大的组合，只是总重量变为了不超过 x - w_i ，如果 x - w_i < 0，我们就从前 i - 1 件物品中选择。因此我们从这两种情况中取较大者作为 S(i, x) 的最优解，表示为：

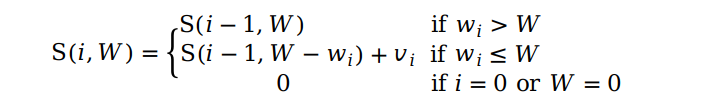
这里我们规定 S(0, x) 和 S(i, 0) 都等于 0，这样我们就用一张 n × W 的二维表来记录每一个子问题的解，并用 0 补全 S(0, x) 和 S(i, 0)。

我们的实例为：W = 10, w₁ = 7, v₁ = 42; w₂ = 3, v₂ = 12; w₃ = 4, v₃ = 40; w₄ = 5, v₄ = 25。 从最简单的子问题 S(1, 1) 开始，显然 1 < w₁，所以 S(1, 1) = S(0, 1) = 0。

随后我们增大 x 的值，直到 x = 7，得出 S(1, 7) = 42。

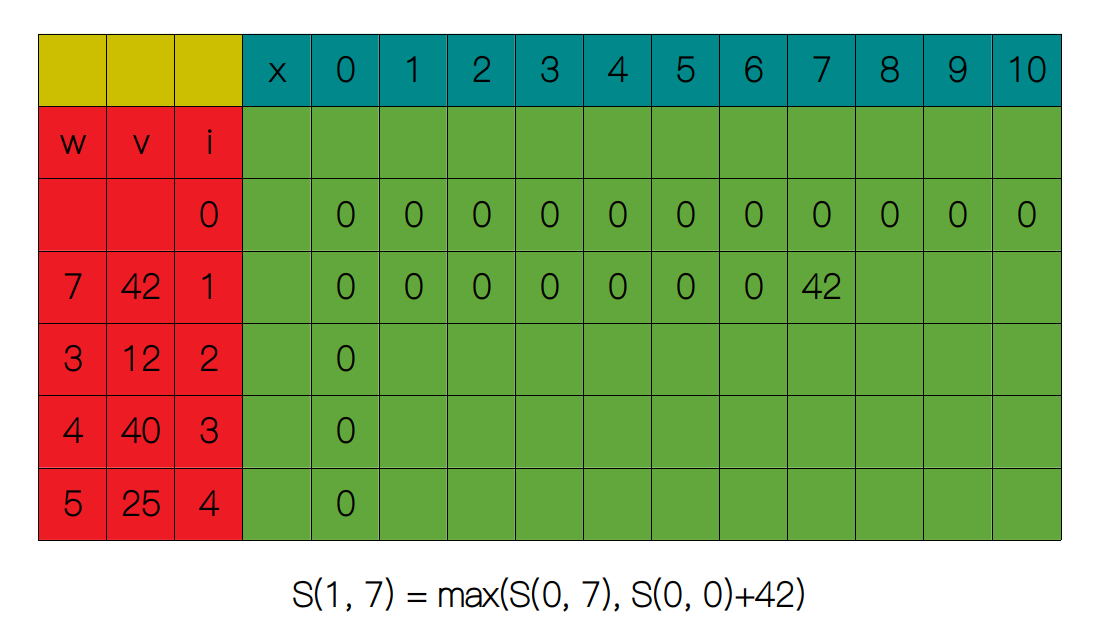
第一行剩下的列我们根据关系式 S(i, x) = max(S(i - 1, x), S(i - 1, x - w_i) + v_i) 填满。

同理，第二行也是从 x = 1 开始，逐渐增加 x 的值，直到 x = 3 时我们得到 S(2, 3) = 12。

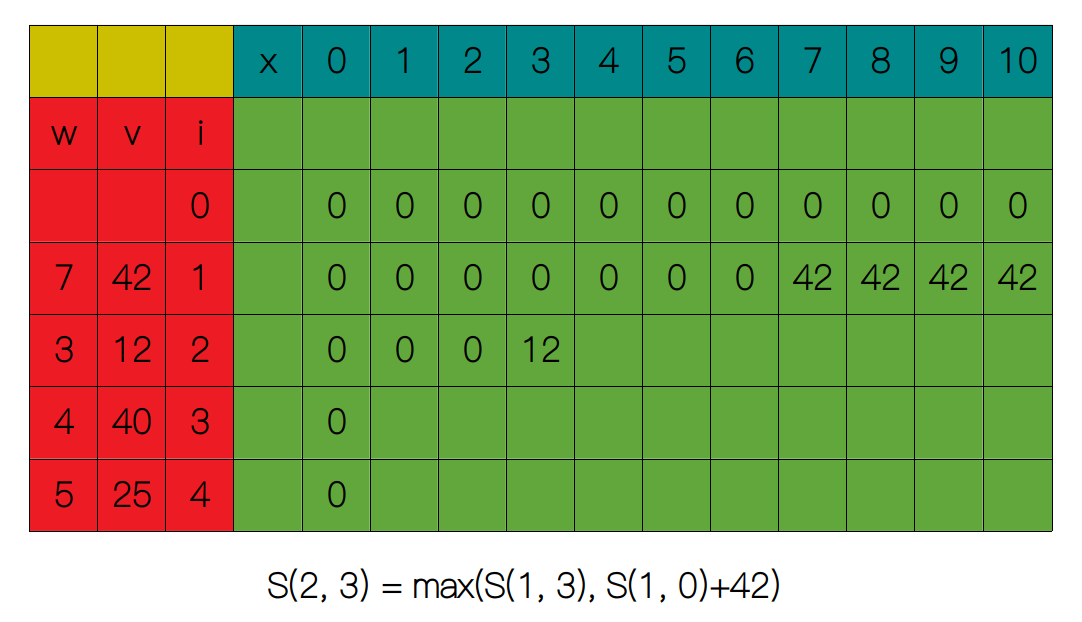
剩下的列同样也是通过关系式 S(i, x) = max(S(i - 1, x), S(i - 1, x - w_i) + v_i) 求得。

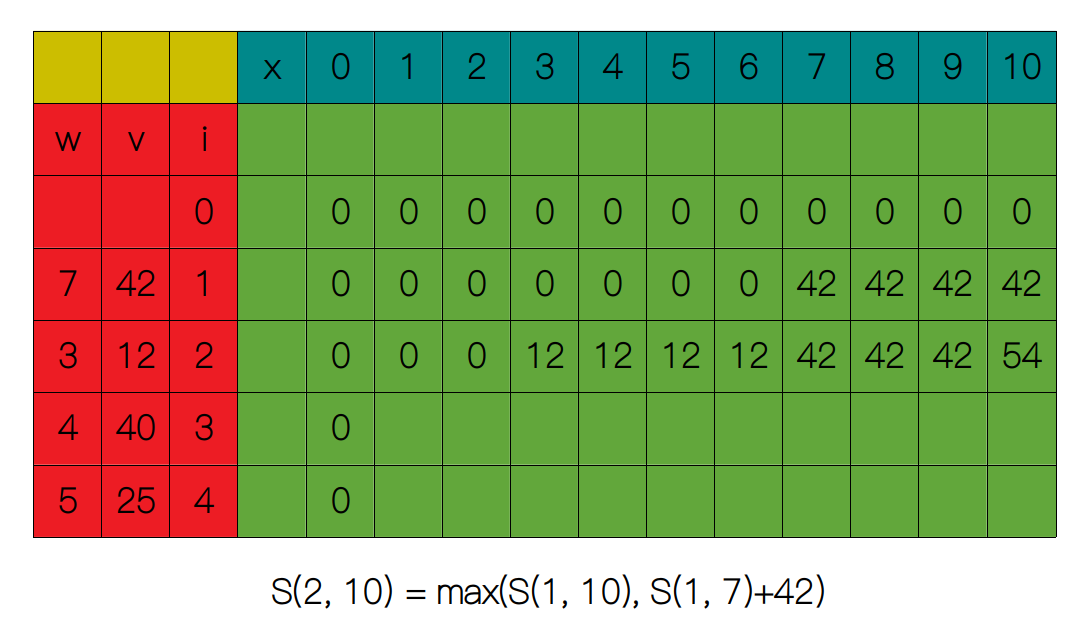
下面的行和列以此类推，直到把整张表填满，最后原问题的最优解为 65。

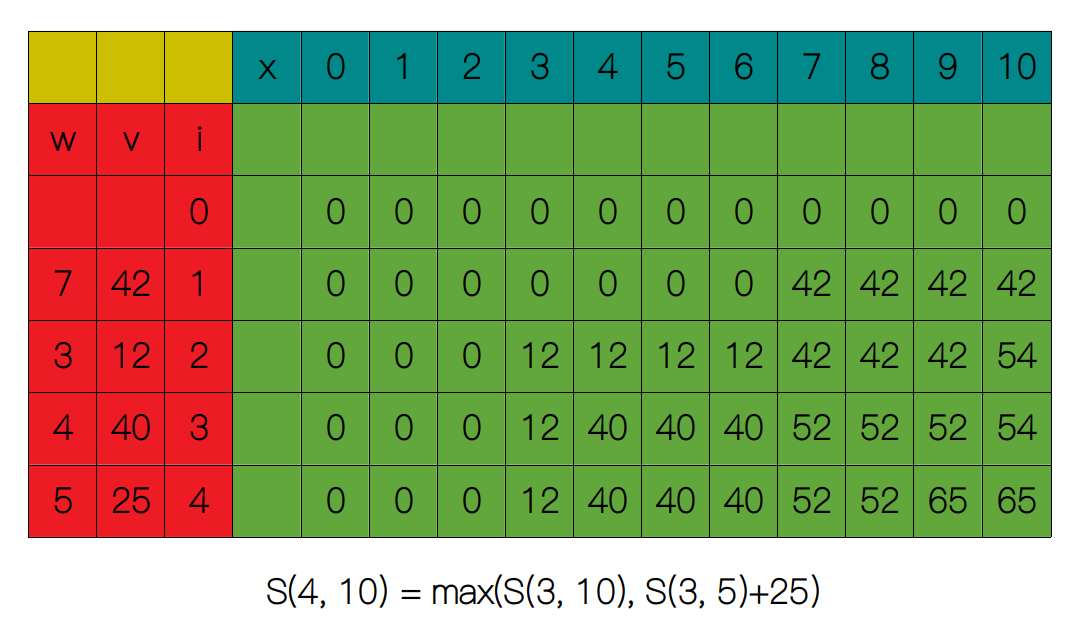
像这样，先从最简单的子问题入手，将子问题的解用一张表存储起来，然后后面复杂的子问题是通过前面子问题的解得出的，我们把这种方法叫做自底向上。

def knapsack_bottom_up(weights, values, capacity):
    n = len(weights)  # 物品数
    table = np.zeros([n+1, capacity+1], dtype=np.int)
    for i in range(1, n+1):
        for j in range(1, capacity+1):
            wi = weights[i-1]; vi = values[i-1]
            if j < wi:
                table[i][j] = table[i-1][j]
            else:
                table[i][j] = max(table[i-1][j], table[i-1][j-wi] + vi)
    return table[n][capacity]

由于需要用到 n × W 的表格，以及计算表格中的每一项，所以自底向上解决背包问题的时间和空间复杂度都为 Θ(nW)。

自顶向下

自顶向下法又叫做备忘录法，它是基于递归来实现的。首先我们还是需要建一个 n × W 的表，并且表中所有项均初始化为 -1，表示该项还没有被计算过，并用 0 补全 S(0, x) 和 S(i, 0)。

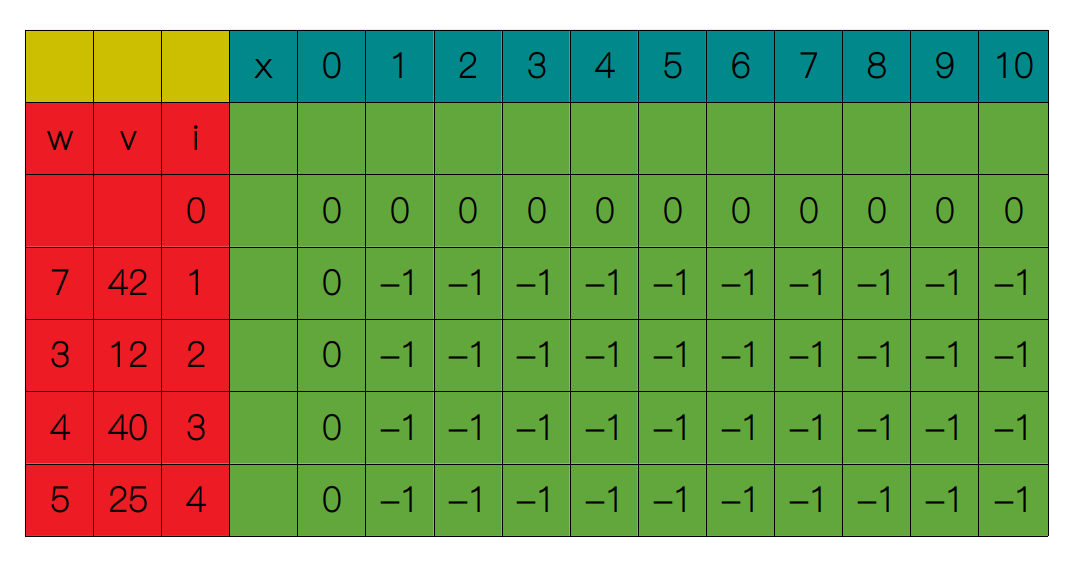
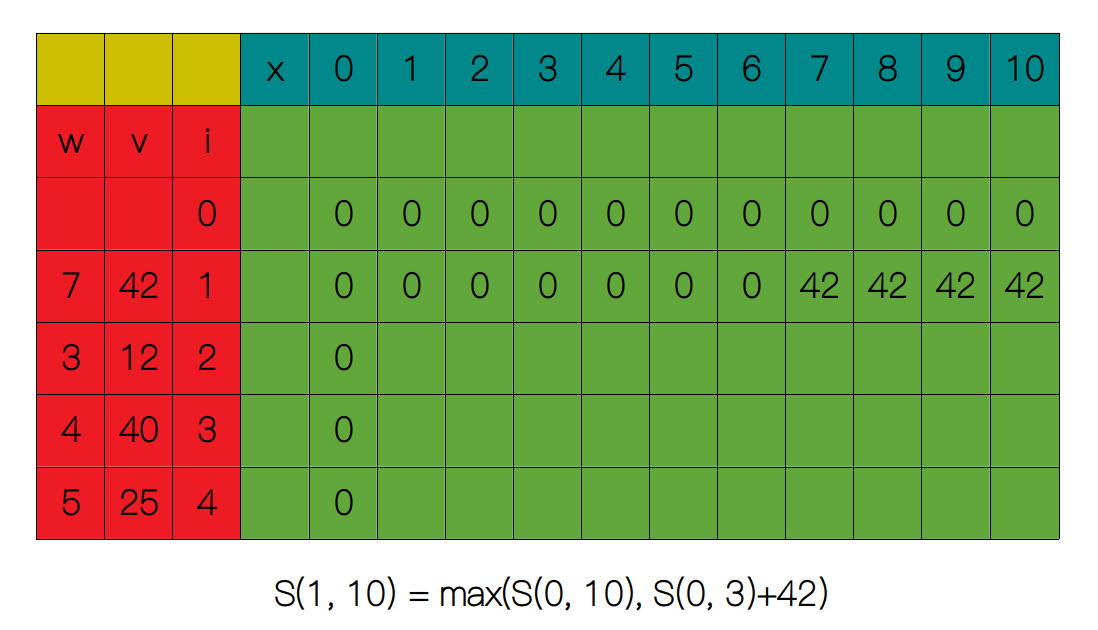
跟自底向上的方法不同的是，自顶向下着眼于原问题的解，然后通过递归的方式搜索子问题的解，如果子问题没有解（表中对应项为 -1），则继续向下搜索直至遇到递归出口（i = 0 或 x = 0），每次子问题从递归出口中得到了求解，我们就将它们记录在表中的相应位置。如果子问题已经存在解，我们就直接用现有的解，以此避免子问题的重复求解，因此这里我们着眼于 S(4, 10)。

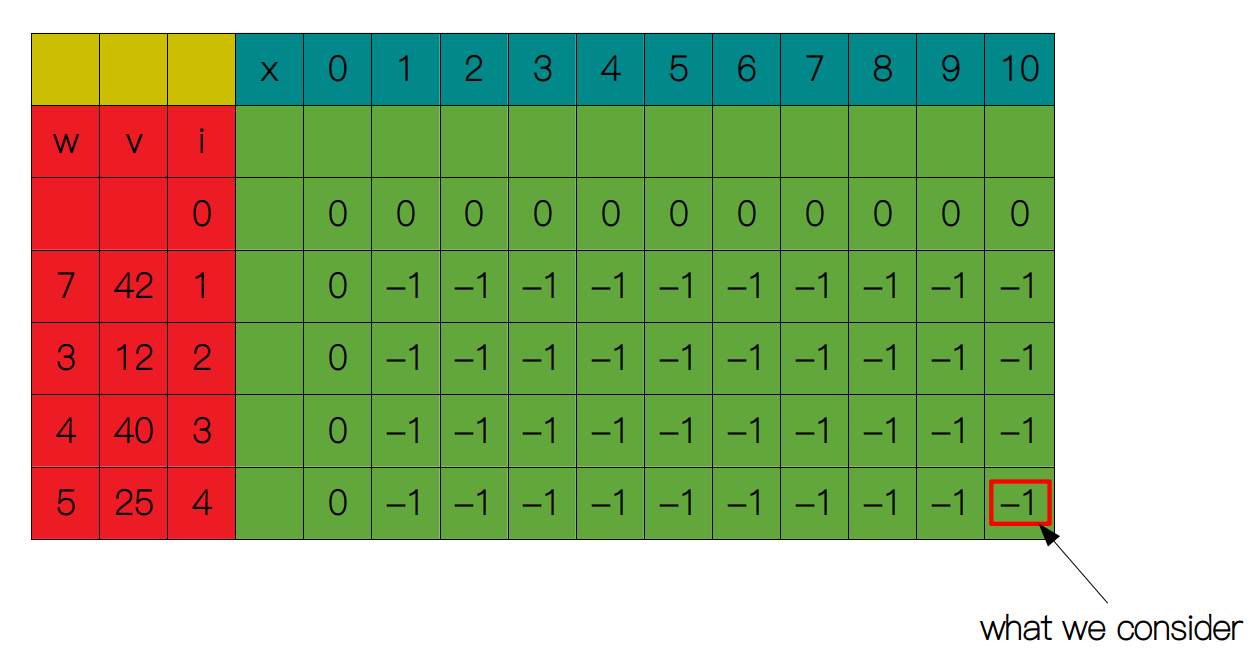
然后我们递归地向下搜索，这里即是从 S(3, 10) 和 S(3, 5) + 25 中取较大者。

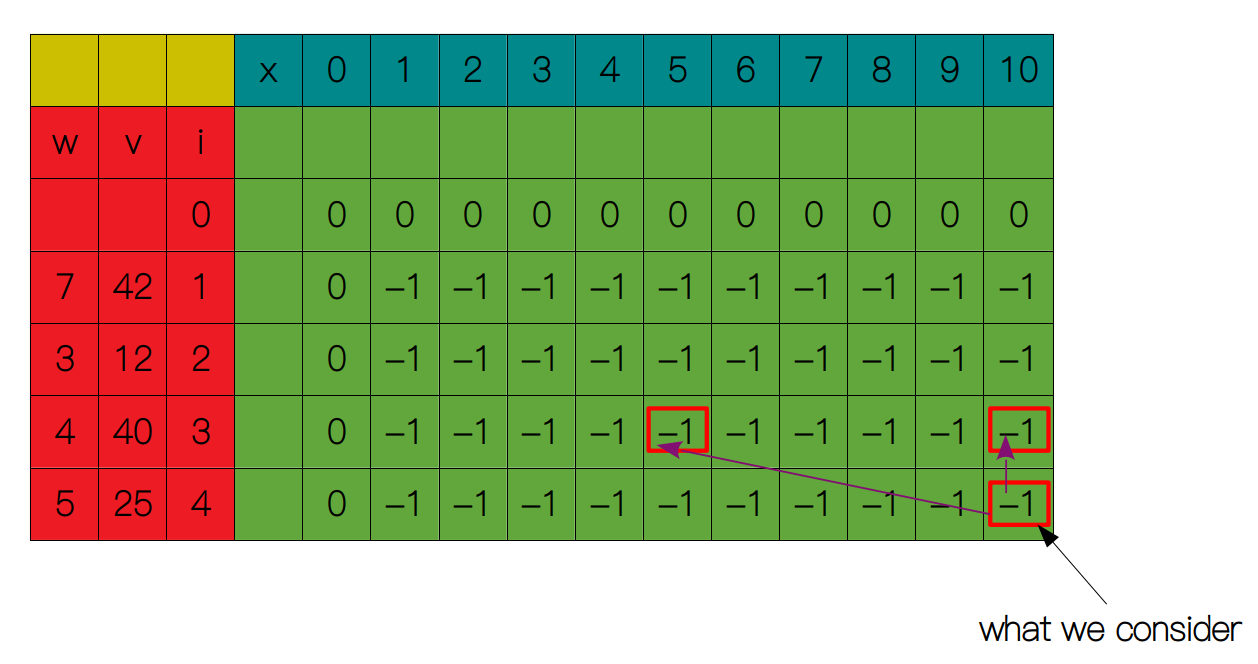
S(3, 10) 和 S(3, 5) 对应表格的值都为 -1，所以我们还要继续向下搜索，一旦遇到递归出口，我们就返回 0。

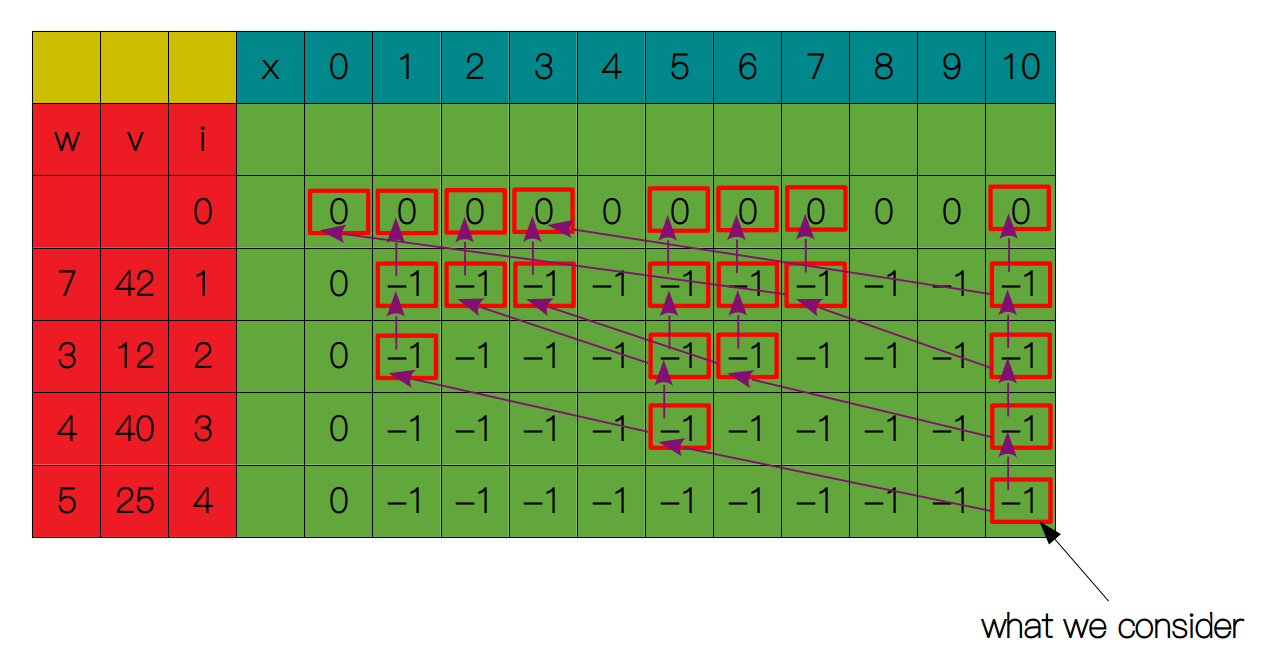
返回后，在表中记录下相应的最优解，以便后面的子问题使用，最后得到原问题的解。

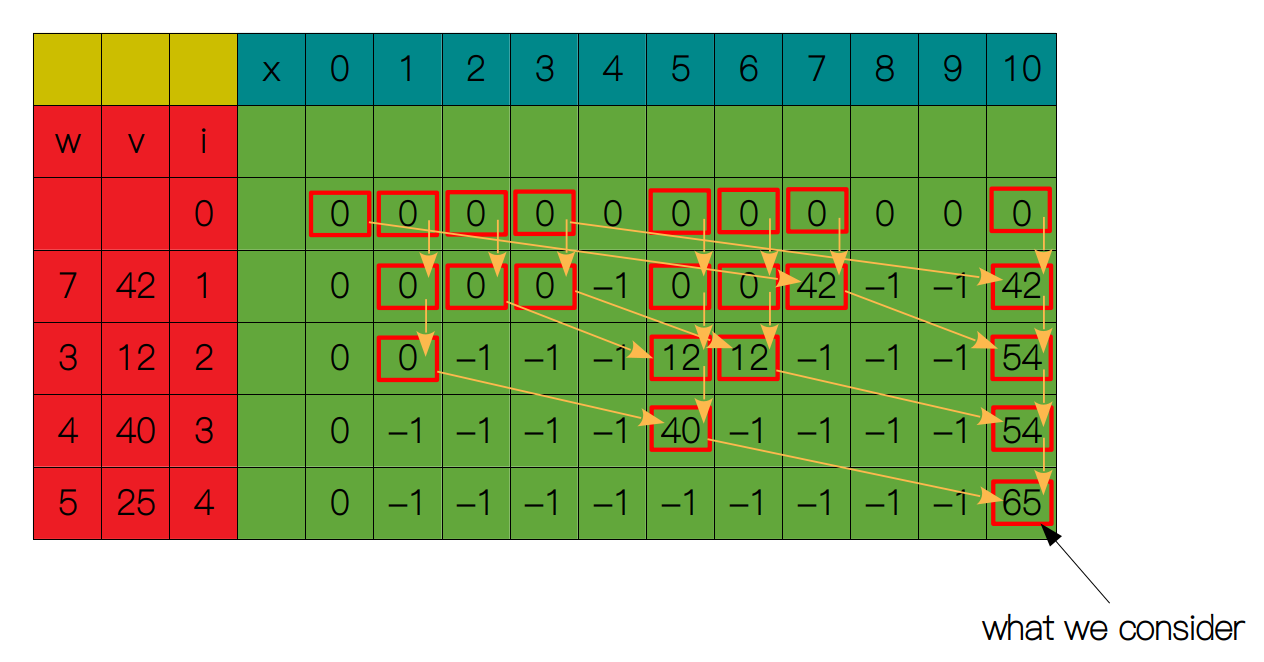
这样就完成了自顶向下的全部过程，下面就是用代码来实现它啦～

def knapsack_top_down(t, w, v, i, j):
    if t[i][j] < 0:
        if j < w[i-1]:
            t[i][j] = knapsack_top_down(t, w, v, i-1, j)
        else:
            t[i][j] = max(knapsack_top_down(t, w, v, i-1, j), knapsack_top_down(t, w, v, i-1, j-w[i-1])+v[i-1])
    return t[i][j]
def knapsack_top_down_main(weights, values, capacity):
    n = len(weights)  # 物品数
    table = np.zeros([n+1, capacity+1], dtype=np.int) - 1
    table[0, :] = 0; table[:, 0] = 0  # 用 0 填满第一行和第一列
    maximum = knapsack_top_down(table, weights, values, n, capacity)
    return maximum

同样，自顶向下解决背包问题的时间和空间复杂度也为 Θ(nW)。但我们可以看到在记录子问题的解的表格中只有那些不为 -1 的项才是真正被计算的部分，所以自顶向下的优势是计算的次数会比自底向上要少，但缺点是递归会造成更多的内存空间的使用。

→ 本节全部代码 ←