图的最短路径
高德地图相信大家一定都用过,每当我们输入一个目的地时,系统总是会帮助我们寻找一条最近的路。我们知道出发地到目的地可能有很多条路可以选择,而高德地图是怎样做到为我们选择更近的路呢?这一节的内容,我们就会来讨论关于图的最短路径的问题。

在计算机里,我们用有权图来表示城市的路网,其中每个节点代表一个地点,每条边代表从一个地方到另一个地方的距离,数据结构我们使用邻接矩阵的形式。
计算最短路径分成两种情况,一种是一次计算所有点对的最短路径,就是下面我们要讲到的弗洛伊德算法;另一种是单源最短路径,也就是计算某一个节点到其他所有节点的最短距离,后面的迪克斯特拉算法采用的就是这种方式。
弗洛伊德算法
从出发地到目的地的过程中,我们并不是一下子就到达目的地,而是要经过很多的中转站来帮助我们一步一步地到达目的地。例如下面的图中,假设 AB,BC 之间的距离分别为 7 和 2。我们看到,A 和 C 之间不能直接通达,因此,要计算 A 和 C 之间的距离,我们就要借助 B 来作为中转站,因此 A 到 C 的距离为 7 + 2 = 9。
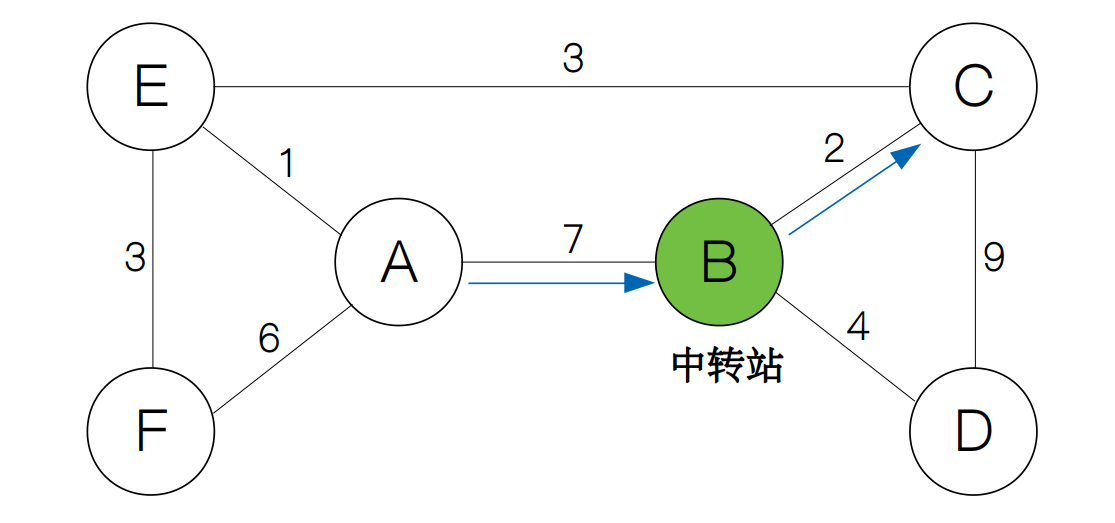
但是,单凭一个中转站在有些情况下也是不行的,比如从 D 到 F 就不能只通过一个中转站。
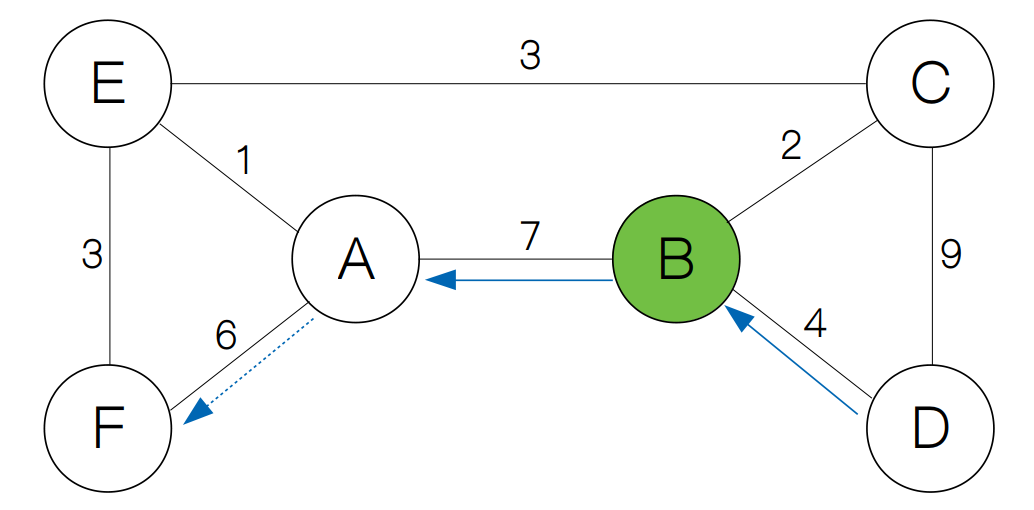
因此,计算所有节点之间的最短距离这个大问题可以分为借助 k 个中转站的情况下计算各节点之间的最短路径,其中 0 ≤ k ≤ |V|。
下面来谈一下具体的求解过程,我们首先用邻接矩阵来表示这张图,其中 ∞ 表示两个节点之间不能相互直达,矩阵中每一项的数字代表边的权重,也就是节点之间的距离。

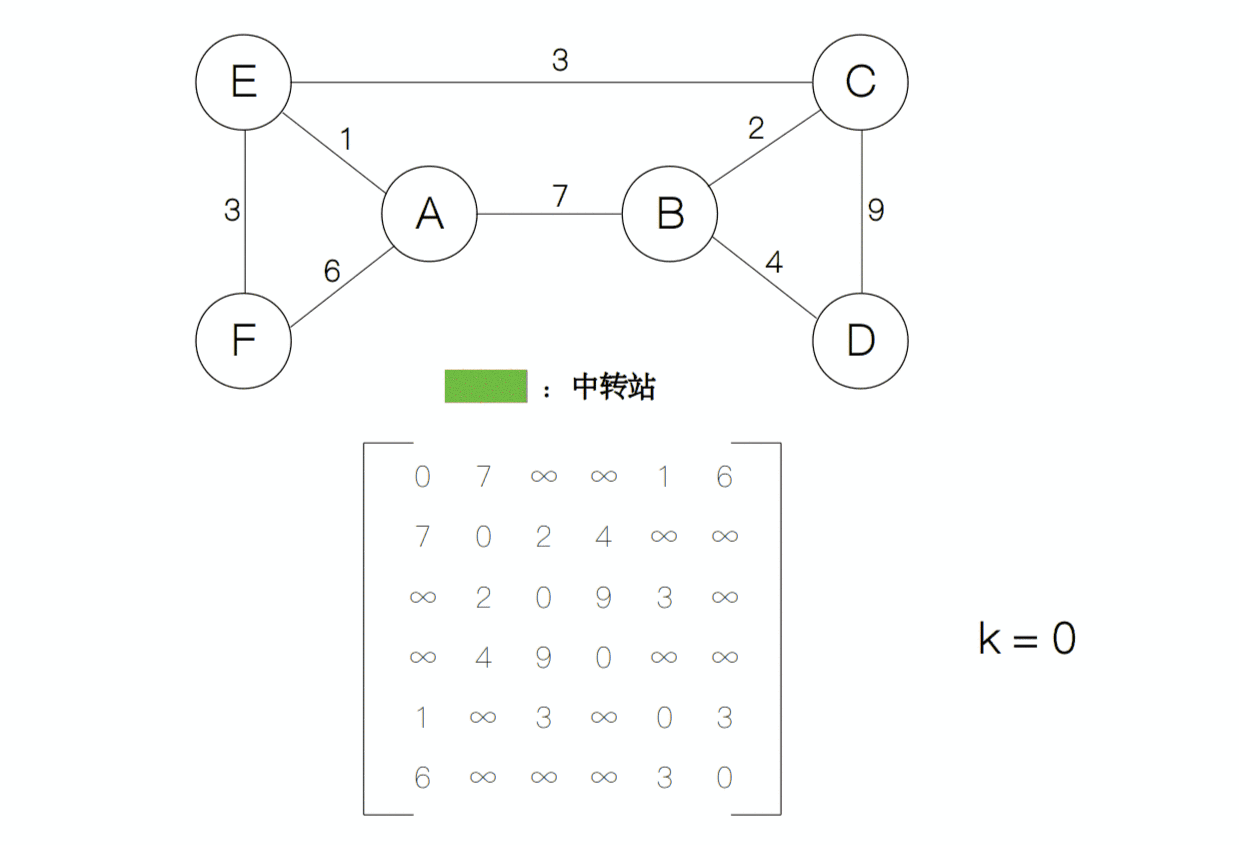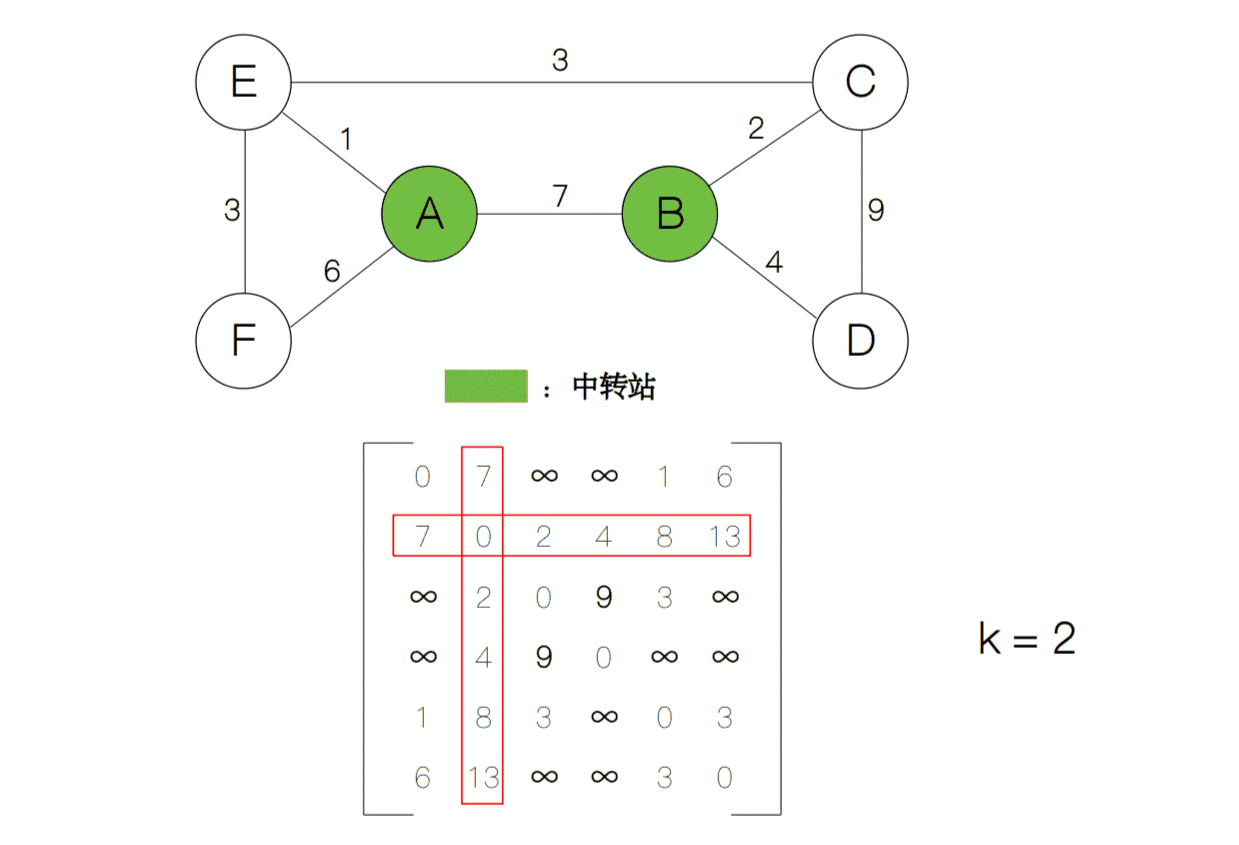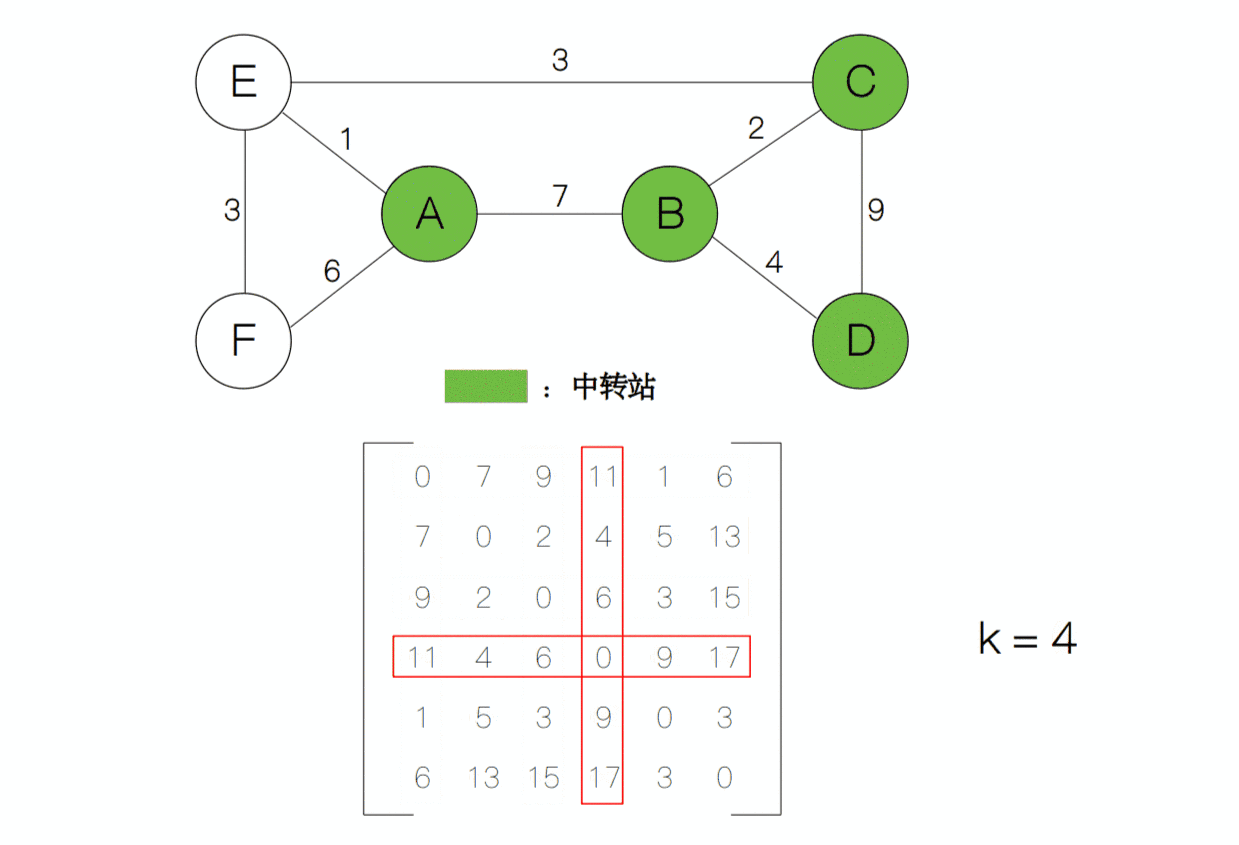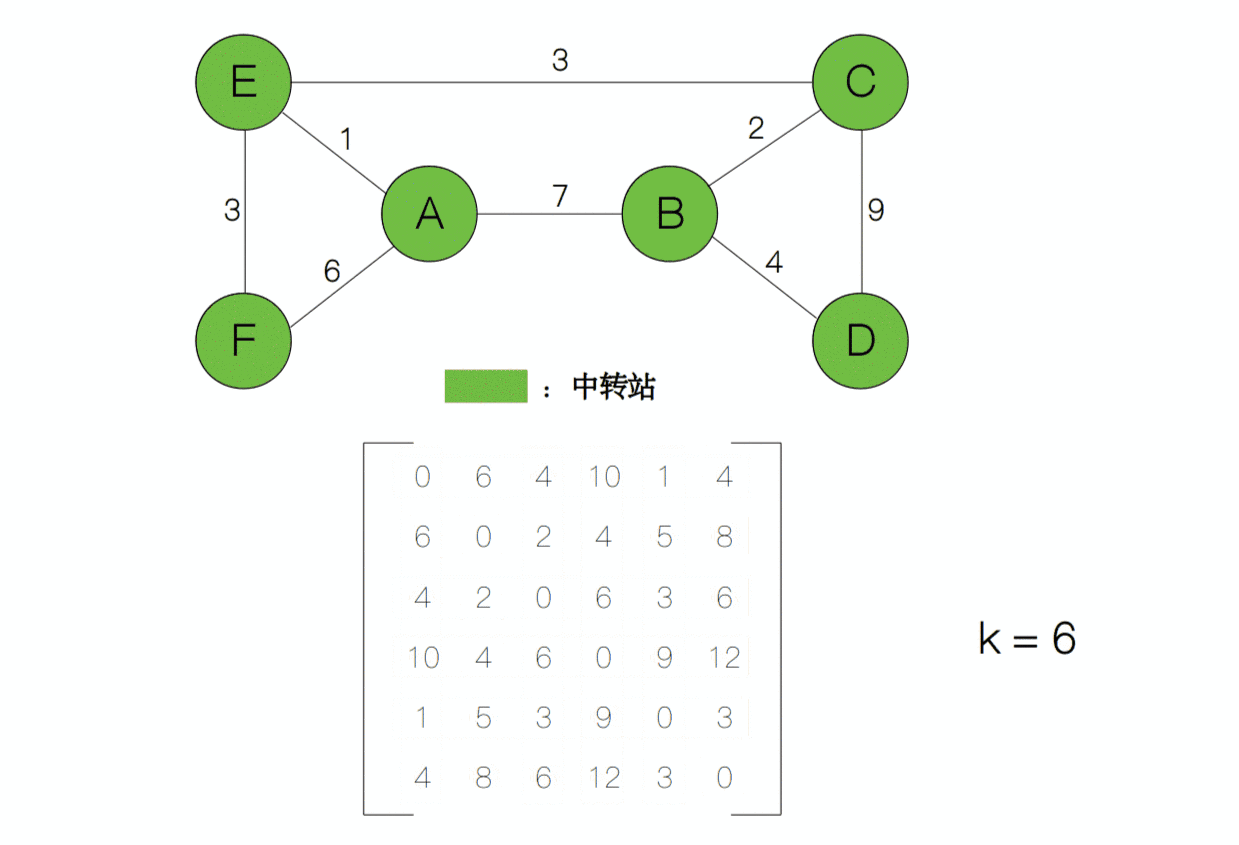
上面的矩阵也可以代表在不借助中转站的情况下(k = 0)各节点之间的最短路径。接下来,我们只让节点 A 作为中转站,然后计算各节点的最短路径,然后对于矩阵的每一项,我们比较d[i][j]和d[i][1]+d[1][j]的大小,然后取最小者作为d[i][j]的值。其中i和j分别代表矩阵的行和列。
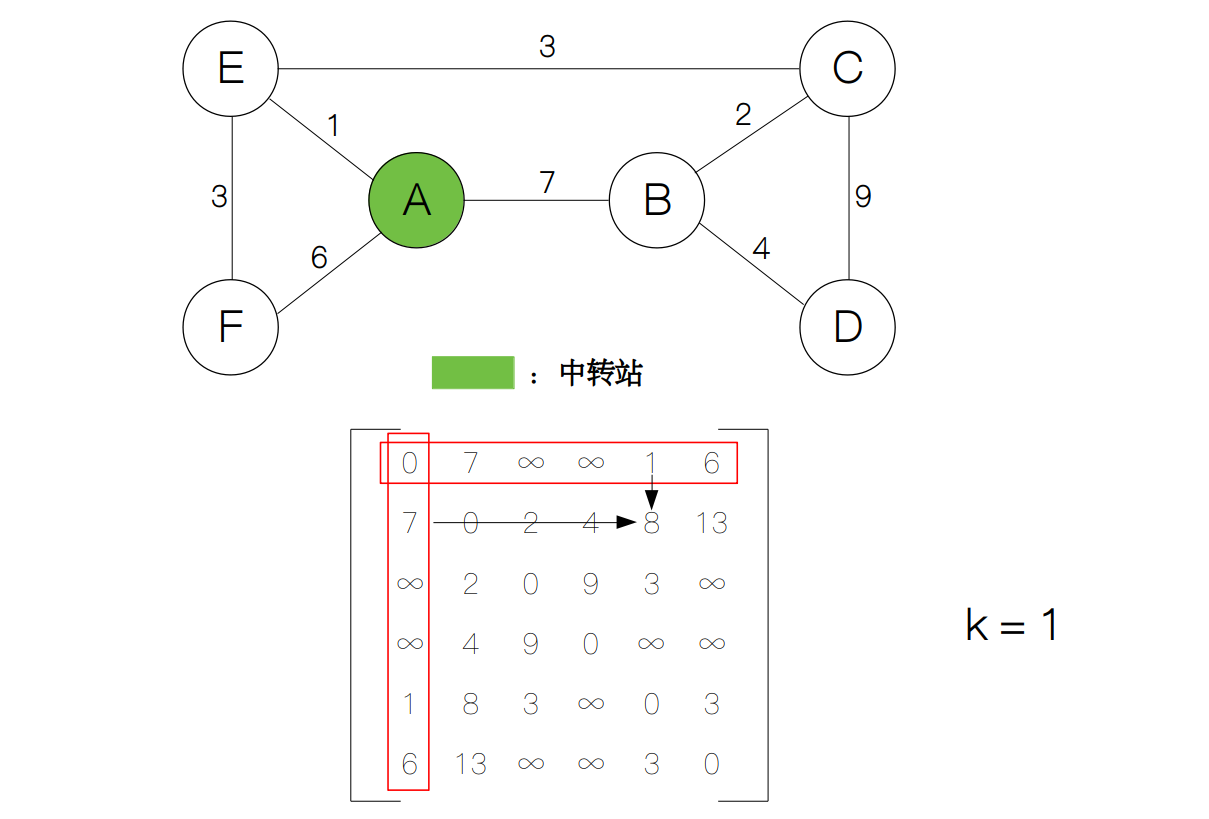
计算后我们发现矩阵中的第 2 行第 5 列从原来的 ∞ 变为了 8,说明从节点 B 到节点 E 的最短距离在当前状态下为 8。接下来,我们逐渐增加中转站的个数,每增加一个中转站的个数,矩阵就更新一次。假设中转站的个数为k,那么它与上一个状态k-1之间存在这样的关系d[i][j] = min(d[i][j], d[i][k] + d[k][j]),于是k从 1 递增到 n,每递增一次,矩阵的值就更新一次,最后我们就得到所有点对的最短距离了。
用代码表示这个过程非常简单,只需要几行就能实现:
def Floyd(d):
n = d.shape[0]
for k in range(n):
for i in range(n):
for j in range(n):
d[i][j] = min(d[i][j], d[i][k]+d[k][j])
return d
最后打印出循环过后的矩阵。
>>> python Floyd.py
>>> [[ 0. 6. 4. 10. 1. 4.]
[ 6. 0. 2. 4. 5. 8.]
[ 4. 2. 0. 6. 3. 6.]
[10. 4. 6. 0. 9. 12.]
[ 1. 5. 3. 9. 0. 3.]
[ 4. 8. 6. 12. 3. 0.]]
例如,第 1 行第 4 列代表从 A 到 E 的最短路径为 10。
由于程序中存在三重循环,所以弗洛伊德算法的时间复杂度为 Θ(n3),而邻接矩阵有 n2 项,因此空间复杂度自然就为 Θ(n2)。
→ 本节全部代码 ←