什么是动态规划
在介绍动态规划(dynamic programming)前,咱们首先要弄清楚一个概念,重叠子问题(overlapping subproblem)。前面我们学到的分治法是将一个大问题分成若干个子问题,然后逐一解决子问题,然后合并子问题的解,从而得到原问题的解。但这里的子问题之间都是相互独立的,不存在任何交集,就像归并排序一样,子序列 a 和子序列 b 的合并不会跟子序列 c 和子序列 d 的合并有任何重叠,反过来也一样。而动态规划就是专门解决问题中含有重叠子问题(子问题 1 包含了子问题 2 的解,子问题 2 又包含了子问题 3 的解)而设计的。你可能会觉得前面的描述有点抽象,下面我们就来举一个简单的例子吧。
斐波那契数列是数学中最常见的数列,它的每一项都等于前两项之和,其中第一项和第二项分别为 0 和 1。根据定义我们很快就能得到下面的式子:
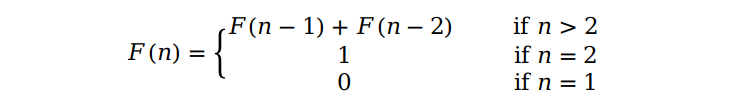
假设要计算 F(5),我们就要先计算 F(4) 和 F(3),而计算 F(4) 又要计算 F(3) 和 F(2),F(3) 又是由 F(2) 和 F(1) 组成等等。稍加观察你就会发现了 F(3) 被计算了两次,从而造成了不必要的重复,影响了最后的效率。
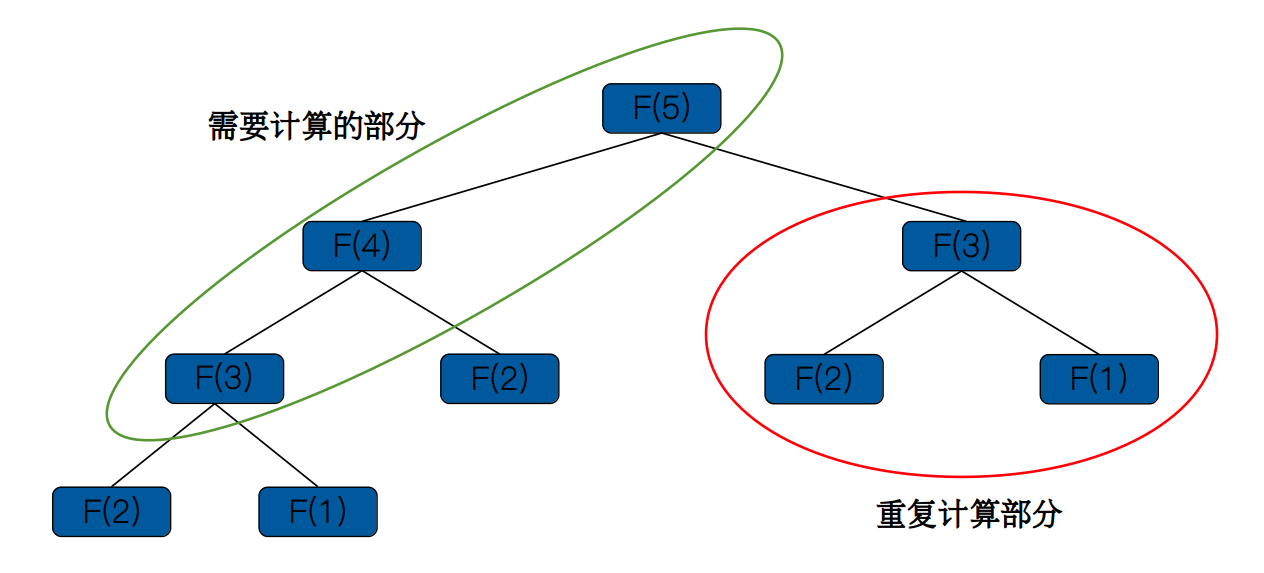
上图中就很好的反映出了重叠子问题这一概念,其中打红圈的部分表示重复计算的部分,而真正需要计算的仅是从左下部分的 F(3) 到顶部的 F(5) 。动态规划的核心思想是将那些本该需要重复计算的部分用一张表暂时存储起来,以便下一次计算的时候直接从表中取出结果,而非再次计算。
既然我们知道 F(1) = 0, F(2) = 1,所以我们便可以计算出 F(3) 的值,并保存在数组中,计算完 F(3) 后,F(4) 又可以根据已有的 F(2) 和 F(3) 被计算出来,这样以此类推,直到计算出 F(n)。
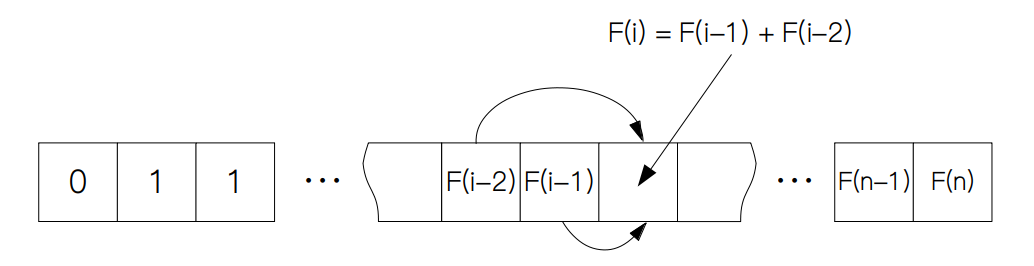
用递归的方式求解斐波那契数列是非常低效的,时间复杂度达到了 Θ(2n)。而如果牺牲空间复杂度为 Θ(n) 来换取时间复杂度的话,我们可以将时间复杂度将降为 Θ(n)。
硬币问题
硬币问题是一道经典的动态规划问题,问题的描述为,在一行面值不同的硬币中选择金额最大的组合,同时保证两个相邻的硬币不能被同时选择。

例如上面的图中,我们可以这样选择:

但不能这样选择:

我们首先来讨论一下用递归求解的方式。很简单,从 n 枚硬币中选择最大金额的问题 F(n) 可以分为两个子问题,取决于我们选不选第 n 枚硬币,如果不选,子问题变为从剩下 n - 1 枚硬币中选择最大金额 F(n-1);如果选了,子问题变为从剩下 n - 2 枚硬币中选择最大金额并加上第 n 枚硬币的面值 F(n-2) + Cn ,最后两者中取其较大者,所以就有关系式 F(n) = max(F(n-1), F(n-2)+Cn)。因此我们写出用递归求解的代码:
def coin_row_bf(coins, n):
if n == 0:
return 0
if n == 1:
return coins[n-1] # 选择第 n 枚硬币
return max(coin_row_bf(coins, n-2), coin_row_bf(coins, n-1) + coins[n-1])
这样做会造成很多子问题被重复地求解,非常低效,时间复杂度达到了指数级 Θ(2n)。下面来看看动态规划是怎样来做的,我们首先从只有一枚硬币说起,毫无疑问,我们要选择它。

如果有两枚呢?我们就会用两种选择,保留第一枚,放弃第二枚,或者保留第二枚,放弃第一枚,在下面的例子中我们选择了第二枚,选择第二枚硬币后,第一枚就不能再选了,因此问题变为了从 0 枚硬币中选择最大的组合,显然没有硬币的时候最大组合为 0,故 F(0) = 0。

如果再加入第三枚面值为 50 的硬币,我们又怎么办呢?前面我们已经得到了 F(n) = max(F(n-1), F(n-2)+Cn) 的关系,所以 F(3) = max(F(2), F(1)+50)。为了不重复计算,我们需要用一个长度为 n 的数组来记录前 i 枚硬币的最优解,在这种情况下,我们就不用再次计算 F(2) 和 F(1) 的值了。因此,我们用一个循环把从 2 到 n 的所有最优解都求出来,最后返回 F(n)。

def coin_row_dp(coins, n):
optima = [-1 for i in range(n+1)]
optima[0] = 0; optima[1] = coins[0]
global combination
for i in range(2, n+1):
# max(F(n-2), F(n-1)+Cn)
if optima[i-1] < optima[i-2] + coins[i-1]:
optima[i] = optima[i-2] + coins[i-1]
else:
optima[i] = optima[i-1]
# 回溯
while n > 0:
if optima[n] > optima[n-1]:
combination[n-1] = 1
n -= 2
else:
n -= 1
return optima[-1]
最后得到其最优解为 130。

因为只用了一个循环,所以时间复杂度就为 Θ(n)。而由于用到了长度为 n 的数组,所以空间复杂度也为 Θ(n)。
找零钱问题
在生活中,找零钱的场景是再熟悉不过了,给定一些面值的钱币,需要凑成一定金额的零钱,怎样凑才能使用到的钱币数最少。

一般情况下,如果需要找的零钱金额为 n,所有钱币的面值为 {d1, d2, …, dm},原问题 F(n) 就可以分为多个子问题:{F(n - di) | 1 ≤ i ≤ m ∧ n - di ≥ 0},每一个子问题又可以再分为几个子问题,直到 n = 0。每递归一次,所需钱币数就 +1,最后我们从子问题集 {F(n - di) | 1 ≤ i ≤ m ∧ n - di ≥ 0} 中寻找最小的组合。因此,F(n) = min({F(n - di) | 1 ≤ i ≤ m ∧ n - di ≥ 0}),所以我们可以写出如下递归关系式:
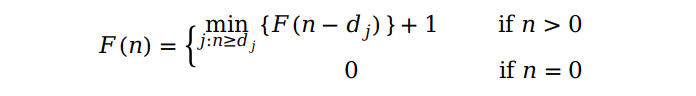
用代码来实现:
def change_making_bf(money, amount):
if amount == 0:
return 0
cnt = inf
for m in money:
if m <= amount:
cnt = min(cnt, change_making_bf(money, amount-m) + 1)
return cnt
这样做还是会造成很多重复性的求解,因此它的时间复杂度还是指数级的 Θ(mn)。
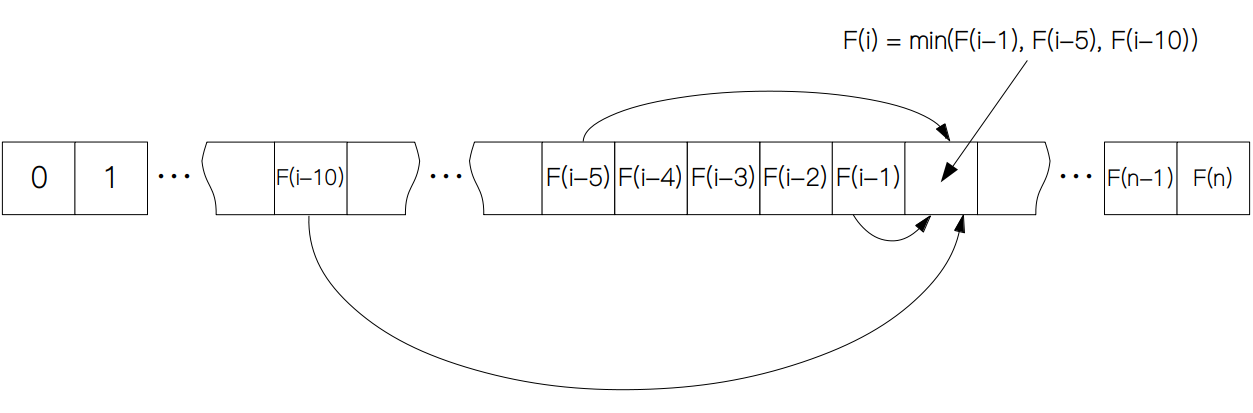
下面来看看动态规划是怎么来做的吧。首先还是需要创建一个表来暂时存放最优解,然后我们计算从 1 到 n 的最优解。举个例子,假设 d = {1, 5, 10},凑齐 0 元我们只需要 0 张钱币,所以 F(0) = 0,而凑齐 1 元我们只有 1 元的面值可用,剩下的面值都大于 1,所以当拿走 1 元后凑齐 1 元的问题就变成了凑齐 0 元的问题,而 F(0) 我们先前计算过,所以 F(1) = 1 + F(0)。后面的 2 到 n 也像前面的那样操作,只是越到后面,我们就越需要从 F(i - 1), F(i - 5), F(i - 10) 中做比较,然后选择最小值。
代码实现:
def change_making_dp(money, amount):
optima = [0 for i in range(amount+1)]
global combination
for i in range(1, amount+1):
temp = inf
j = 0
while j < len(money) and i >= money[j]:
temp = min(temp, optima[i-money[j]])
j += 1
optima[i] = temp + 1
# 回溯
while amount > 0:
temp = inf; idx = 0
for k in range(len(money)):
if amount-money[k] < 0:
break
if optima[amount-money[k]] < temp:
temp = optima[amount-money[k]]
idx = k
combination.append(money[idx])
amount -= money[idx]
return optima[-1]
因为for循环内每循环一次就需要执行 m 次的比较操作,来选择最小的 F(n - di),所以用动态规划来解决找零钱问题的时间复杂度为 Θ(mn),而空间复杂度为 Θ(n)。
我们可以看到,动态规划能够大大提高算法的效率,当然这也离不开要以牺牲内存空间来作为代价。所以,动态规划可以看做“带有缓存的分治法”(来源于知乎)。
→ 本节全部代码 ←