介绍
上一节的内容中,我们讨论了 AVL 这种自平衡的树,不知道各位小伙伴有没有真正理解这种神奇的操作呢?哈哈,在这一节中,你将会遇到更神奇,同时也更复杂的算法来帮助我们平衡二叉树。下面就让我们的红黑树浓重登场吧!
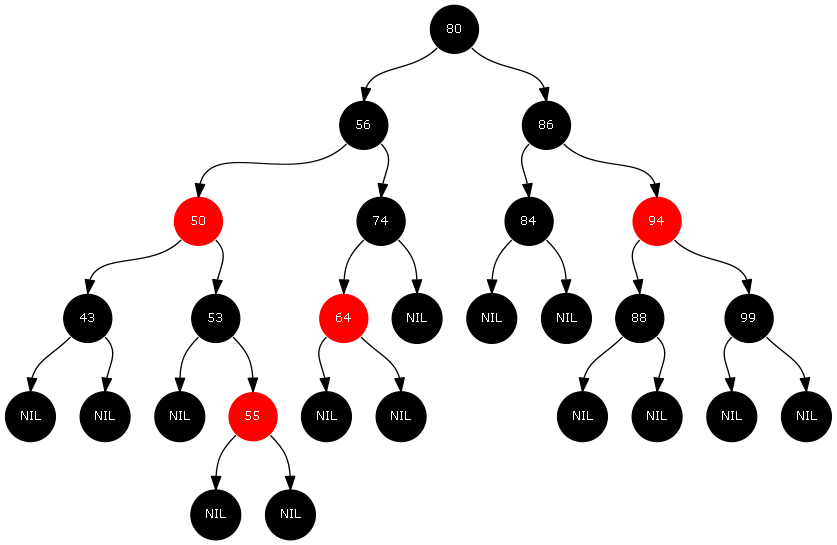
红黑树(red-black tree)也是自平衡的二叉树,在介绍它是如何做到自平衡之前,我们首先来了解一下它的性质。
- 性质 1:所有节点必须为红色或黑色
- 性质 2:根节点为黑色
- 性质 3:所有叶子节点(NIL)为黑色
- 性质 4:如果节点为红色,那么其孩子节点(包括 NIL)必须为黑色
- 性质 5:任意一个节点到每个叶子节点所经过的路径包含相同的数目的黑色节点
红黑树每插入或删除一个节点,都会检查是否违反了上述的性质。如果违反,红黑树就做出相应的操作使树保持平衡,但和 AVL 树不同的是,红黑树不但继承了 AVL 树的旋转操作,还可以通过节点的颜色变换使之不违反上述的五条性质,下面我们就分别来介绍一下这两种操作。
旋转操作
红黑树的旋转操作与 AVL 树的旋转操作是基本上一样的,唯一的不同是每一个节点都对应自己的父节点,因此涉及指针的操作会有所不同。
因此下面我们定义出 Node 类,其中包含了获取祖父节点,叔父节点和兄弟节点的操作。
class Node(object):
def __init__(self, value):
self.value = value
self.color = 'r'
self.left = None
self.right = None
self.parent = None
# 获取祖父节点
def grandparent(self):
if not self.parent:
return None
return self.parent.parent
# 获取叔父节点
def uncle(self):
if not self.grandparent():
return None
if self.parent is self.grandparent().left:
return self.grandparent().right
else:
return self.grandparent().left
# 获取兄弟节点
def brother(self):
if self.parent.left is self:
return self.parent.right
else:
return self.parent.left
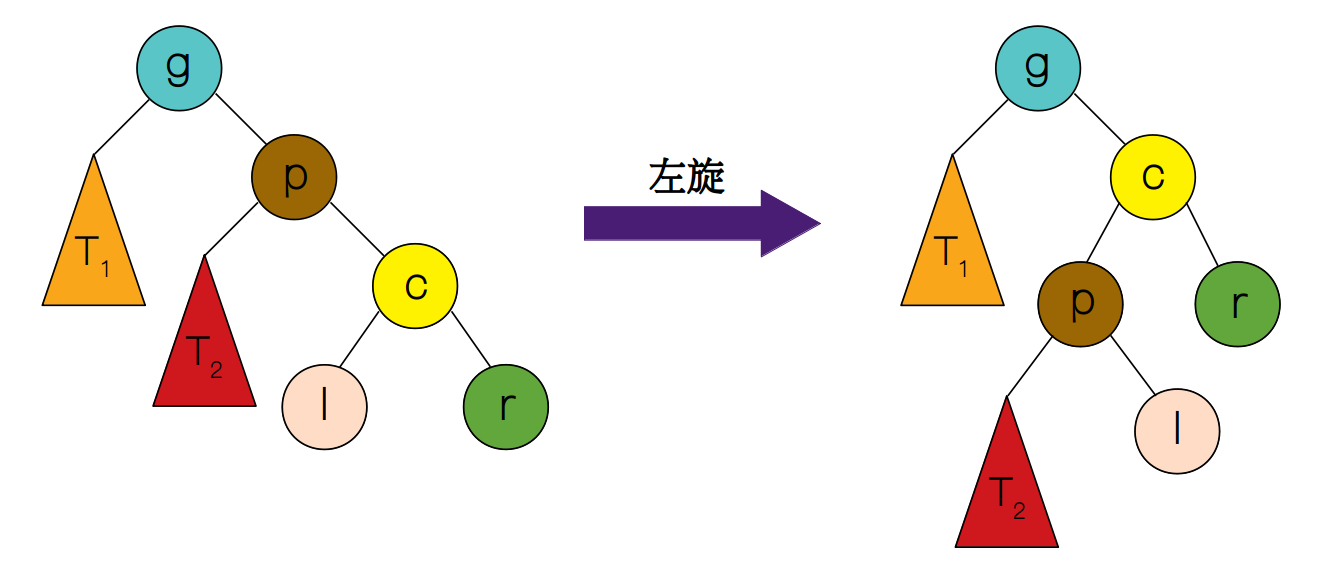
左旋
如下图所示,c 代表旋转节点,g 代表祖父节点,p 代表父节点,l 和 r 分别代表 c 的左孩子和右孩子。经过一次左旋后,原来的 c 节点成为了 g 的右孩子,原来的 p 节点成为了 c 节点的左孩子,并且成为 c 节点的左孩子的父节点。
def left_rotation(self, node):
# node 为根节点
if not node.parent:
self.root = node
return
grandparent = node.grandparent()
parent = node.parent
t = node.left
parent.right = t
# 判断 t 是否为叶子节点
if t is not self.NIL:
t.parent = parent
node.left = parent
parent.parent = node
# 判断父节点是否为根节点
if parent is self.root:
self.root = node
node.parent = grandparent
# 判断祖父节点是否为空
if grandparent:
# 父节点为祖父节点的左孩子
if grandparent.left is parent:
grandparent.left = node
# 父节点为祖父节点的右孩子
else:
grandparent.right = node
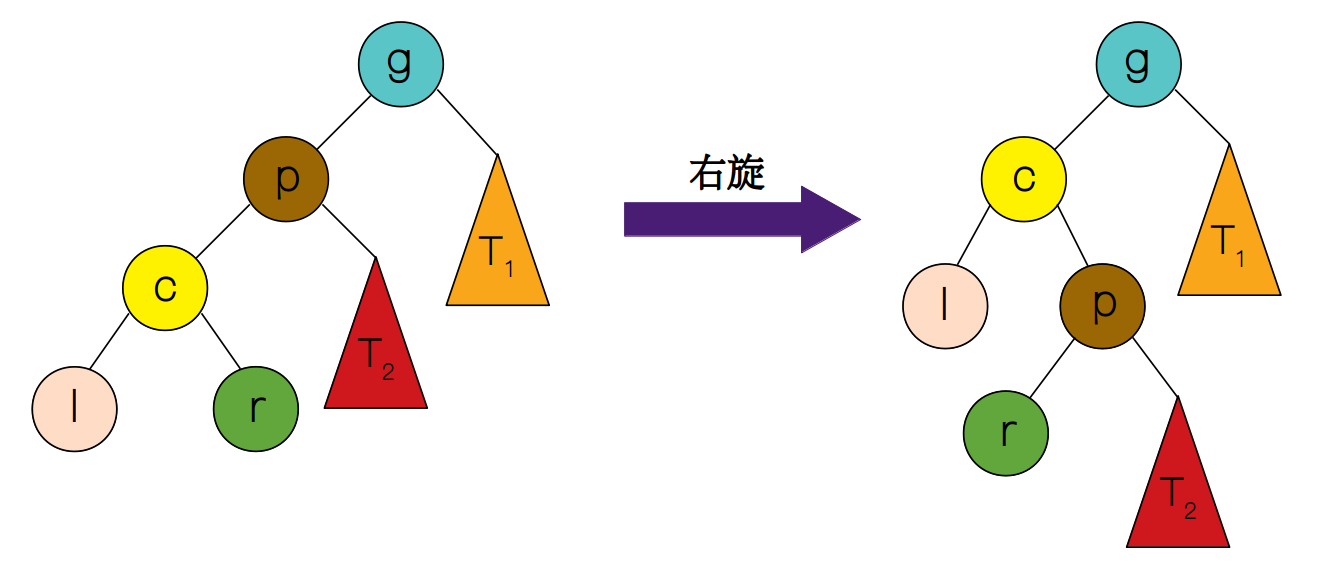
右旋
同理,右旋的操作跟左旋几乎一模一样,只是与左旋互为镜像。下图展示了右旋的全过程。
def right_rotation(self, node):
# node 为根节点
if not node.parent:
self.root = node
return
grandparent = node.grandparent()
parent = node.parent
t = node.right
parent.left = t
# 判断 t 是否为叶子节点
if t is not self.NIL:
t.parent = parent
node.right = parent
parent.parent = node
# 判断父节点是否为根节点
if parent is self.root:
self.root = node
node.parent = grandparent
# 判断祖父节点是否为空
if grandparent:
# 父节点为祖父节点的左孩子
if grandparent.left is parent:
grandparent.left = node
# 父节点为祖父节点的右孩子
else:
grandparent.right = node
和 AVL 树一样,旋转操作只涉及了指针操作,因此不管是左旋还是右旋都是 Θ(1) 的复杂度。
颜色变换
当红黑树插入或删除一个节点时,难免会违反前面五种性质中的一条或多条,在这种情况下,我们就不需要每次都像 AVL 树那样进行麻烦的旋转操作了,而是采取颜色变换的方式,以此来减小因旋转而带来的时间开销。
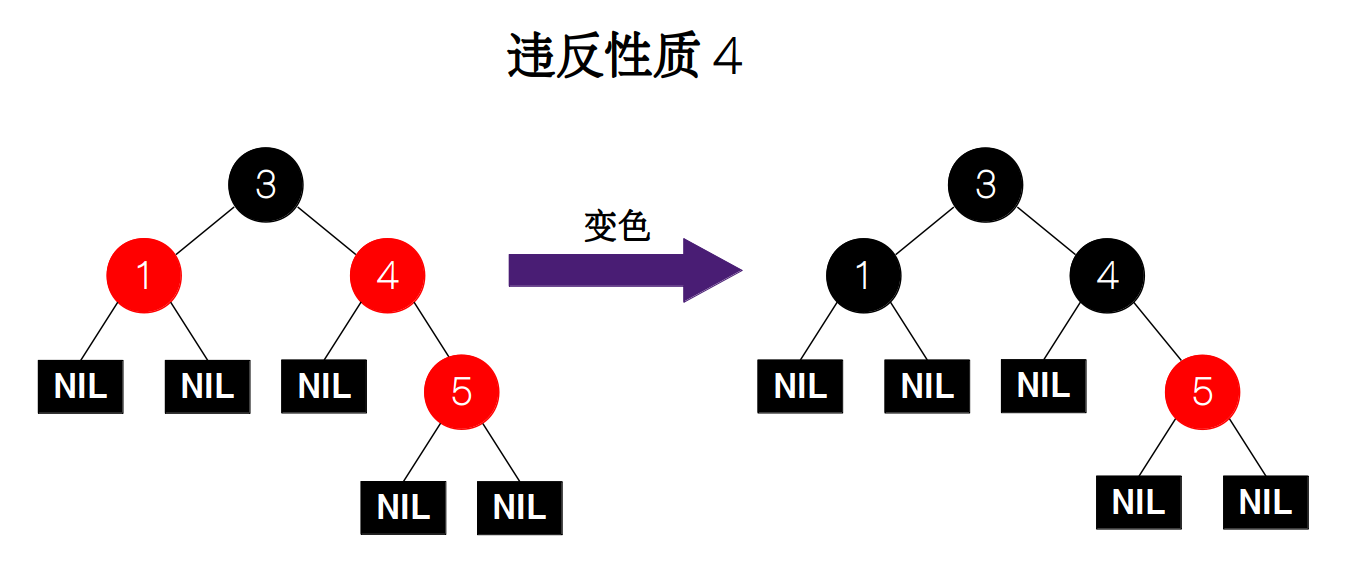
例如,下图中违反了性质 4,我们只需要调整其中一些节点的颜色就能再次满足该性质。
再比如,下图中违反了性质 5,同样也只需调整节点的颜色就能保证再次满足该性质。

颜色变换不涉及任何的运算,因此时间复杂度为 Θ(1)。
搜索
同二叉搜索树一样,红黑树的搜索也是从根节点出发,比较搜索元素与根节点值的大小,然后决定是直接返回该节点,还是从左(右)子树中继续搜索。如果一直搜索到 NIL 节点都还是搜索失败,那么就返回None。
def search(self, value):
# 树的根节点为空就抛出异常
if not self.root:
raise ValueError("The tree is null")
return self.search_node(self.root, value)
def search_node(self, root, value):
if root is self.NIL: # 如果是叶子节点 NIL,则返回 None
return None
if value < root.value: # 从左子树中查找
return self.search_node(root.left, value)
elif value > root.value: # 从右子树中查找
return self.search_node(root.right, value)
else:
return root
由于红黑树是一棵近似的平衡二叉树,故搜索的时间复杂度为 Θ(log n)。
插入
插入操作的前序步骤也和二叉搜索树一样,先找到插入节点的位置,创建一个新的节点,最后使该节点指向其父节点,父节点指向新插入的节点。
def insert(self, value):
# 每个新节点均有两个叶子节点 NIL
new_node = Node(value)
new_node.left = self.NIL
new_node.right = self.NIL
if not self.root:
self.root = new_node
new_node.color = 'b' # 根节点的颜色置为黑色
else:
self.insert_node(self.root, new_node)
def insert_node(self, root, node):
# 搜索
if node.value < root.value:
if root.left is not self.NIL:
self.insert_node(root.left, node)
else:
root.left = node
node.parent = root
self.insert_case(node)
else:
if root.right is not self.NIL:
self.insert_node(root.right, node)
else:
root.right = node
node.parent = root
self.insert_case(node)
完成插入后,我们需要判断新的红黑树有没有违反上面的 5 种性质,如果违反了,就根据不同的情况,做出相应的旋转或变色操作。下面我们就分情况来讨论一下。
- 情况 1:根节点为红色。由于违反了性质 2,所以当根节点的颜色为红色时,我们需要将颜色调整为黑色。
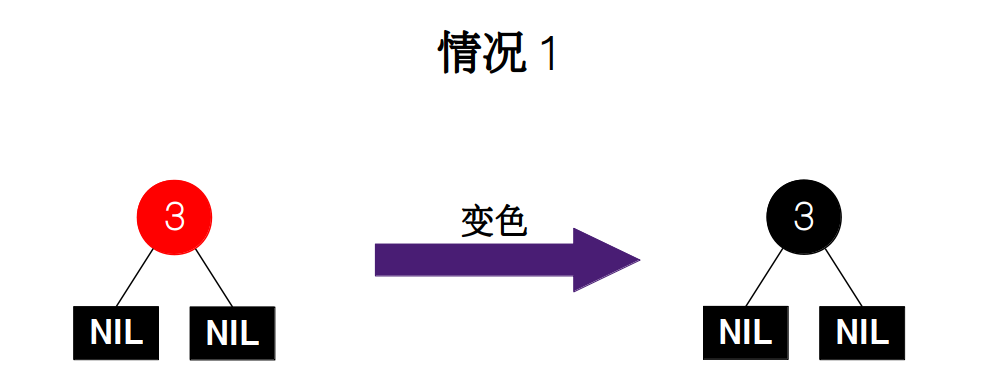
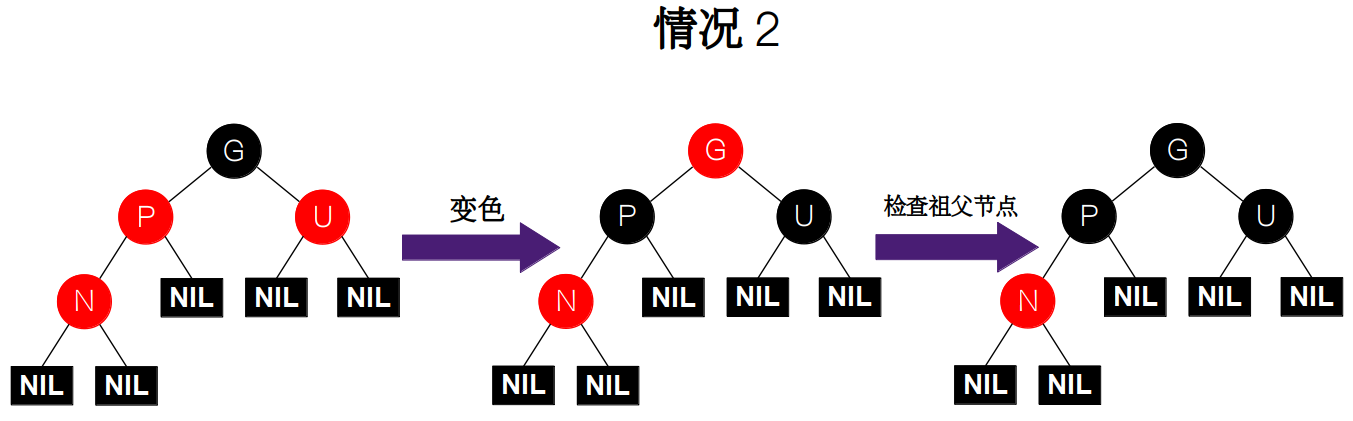
- 情况 2:父节点 P 和叔父节点 U 都为红色,祖父节点 G 为黑色,因为新加入的节点 N 为红色,所以违反了性质 4。因此做出的调整是交换父节点和叔父节点的颜色。因为我们不能保证祖父节点的父节点的颜色是否也为红色,所以我们需要在祖父节点 G 上递归地对情况 2 的进行检查。
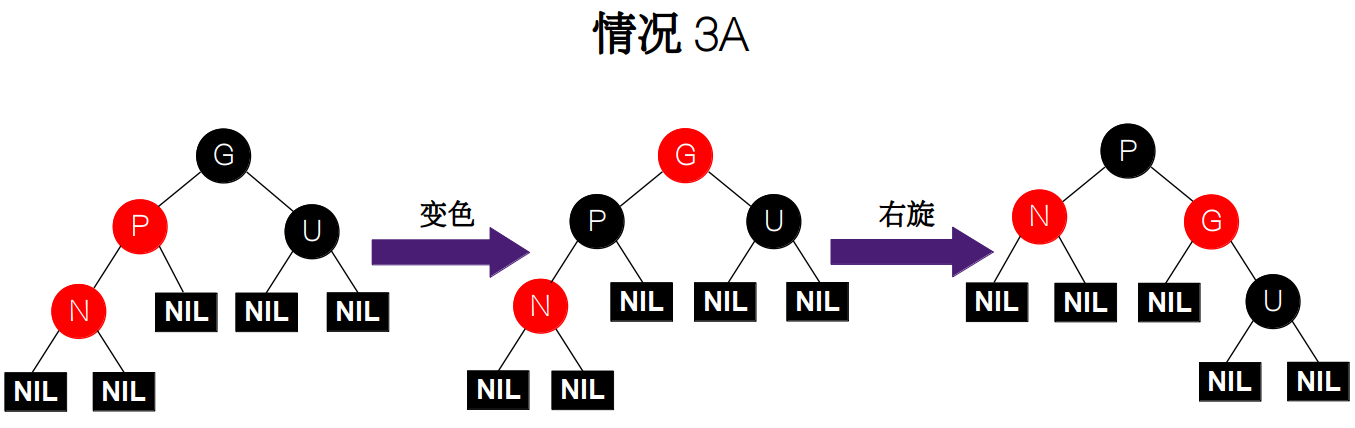
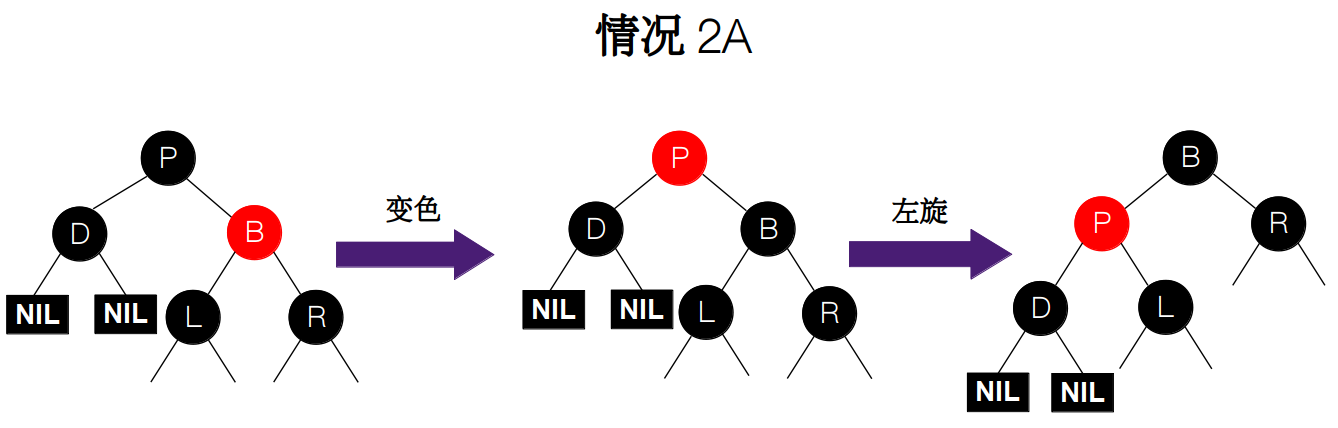
情况 3:父节点 P 为红色,叔父节点 U 为黑色或 NIL,且新插入的节点 N 与父节点和祖父节点在同一侧(G 的左(右)孩子为 P,P 的左(右)孩子为 N)。故我们再把情况 3 分为两种情况:
i) 祖父节点 G 的左孩子为父节点 P,父节点 P 的左孩子为新插入节点 N。此时,我们需要先交换父节点 P 和祖父节点 G 的颜色,然后对 P 进行右旋。
![情况 3A]()
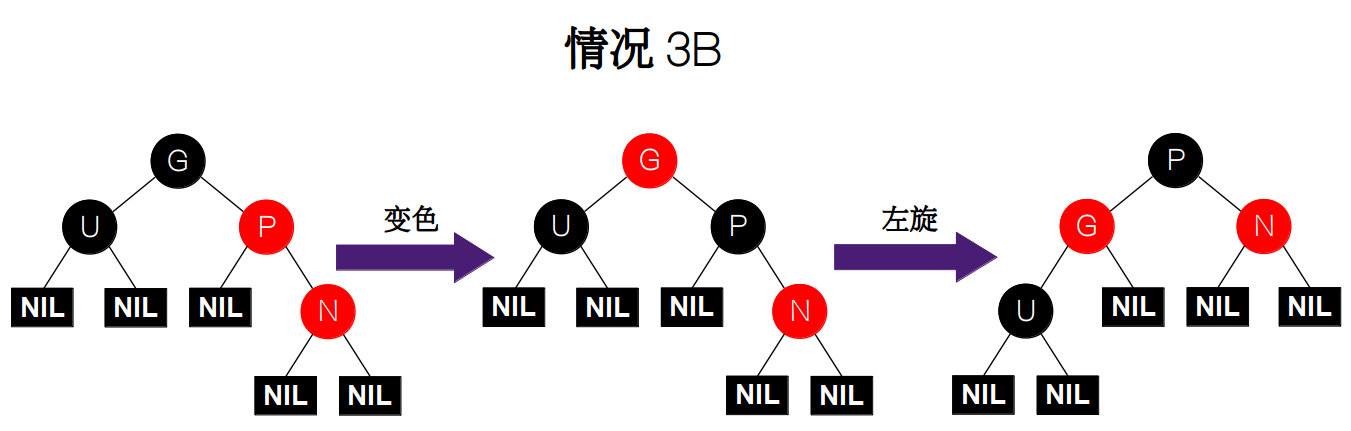
ii) 同理,如果祖父节点 G 的右孩子为父节点 P,父节点 P 的右孩子为新插入节点 N。我们还是要先交换父节点 P 和祖父节点 G 的颜色,然后对 P 进行左旋操作。
![情况 3B]()
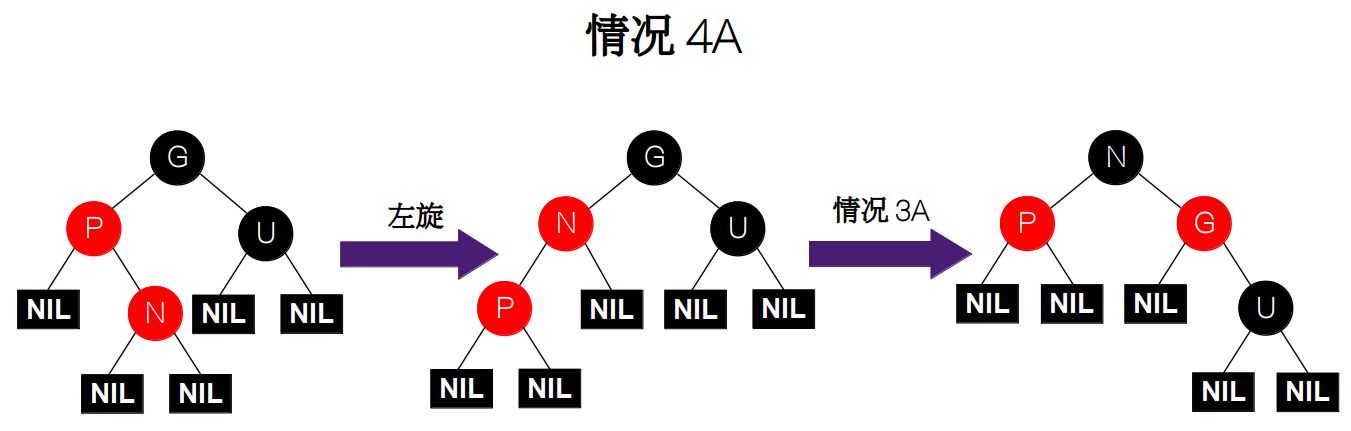
情况 4:父节点 P 为红色,叔父节点 U 为黑色或 NIL,且新插入的节点 N 与父节点和祖父节点不在同一侧(G 的左(右)孩子为 P,P 的右(左)孩子为 N)。故我们还是把情况 4 分为两种情况:
i) 祖父节点 G 的左孩子为父节点 P,父节点 P 的右孩子为新插入节点 N。此时,我们先要对新插入节点 N 执行一次左旋操作,这样就变换为了跟情况 3A 一样的情形,接下来我们只需要再调用情况 3A 即可,只是旋转的节点从父节点 P 变为了新插入节点 N。
![情况 4A]()
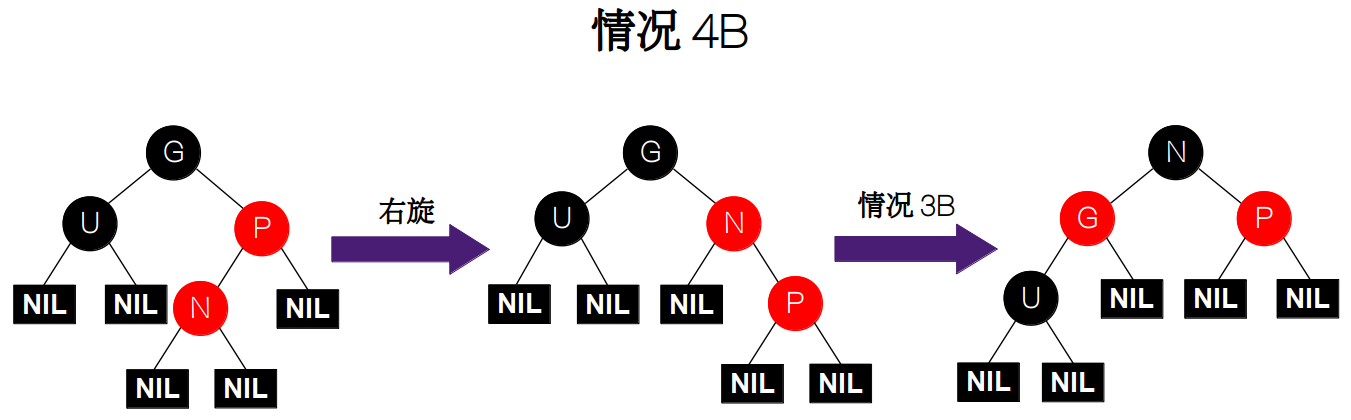
ii) 同样,如果祖父节点 G 的右孩子为父节点 P,父节点 P 的左孩子为新插入节点 N。我们还是先要对新插入节点 N 执行一次旋转操作,只是这里变为了互为镜像的右旋。旋转后就变为了情况 3B,因此接下来我们只需要再调用一次 3B 即可,只是旋转的节点从父节点 P 变为了新插入节点 N。
![情况 4B]()
我们把所有的情况用一个函数insert_case来表示。
def insert_case(self, node):
# 情况 1: 根节点为红色
if not node.parent:
self.root = node
node.color = 'b'
return
# 情况 2: 父节点和叔父节点为红色,祖父节点为黑色。
if node.parent.color == 'r':
if node.uncle().color == 'r':
node.parent.color = 'b'; node.uncle().color = 'b'
node.grandparent().color = 'r'
self.insert_case(node.grandparent()) # 对祖父节点递归地调用 insert_case()
else:
# 情况 3A: 叔父节点为黑色或 NIL,祖父节点的左孩子为父节点,父节点的左孩子为新插入节点
if node.parent.left is node and node.parent is node.grandparent().left:
node.parent.color = 'b'
node.grandparent().color = 'r'
self.right_rotation(node.parent)
# 情况 3B: 叔父节点为黑色或 NIL,祖父节点的右孩子为父节点,父节点的右孩子为新插入节点
elif node.parent.right is node and node.parent is node.grandparent().right:
node.parent.color = 'b'
node.grandparent().color = 'r'
self.left_rotation(node.parent)
# 情况 4A: 叔父节点为黑色或 NIL,祖父节点的左孩子为父节点,父节点的右孩子为新插入节点
elif node.parent.right is node and node.parent is node.grandparent().left:
node.color = 'b'
node.grandparent().color = 'r'
self.left_rotation(node)
self.right_rotation(node)
# 情况 4B: 叔父节点为黑色或 NIL,祖父节点的右孩子为父节点,父节点的左孩子为新插入节点
elif node.parent.left is node and node.parent is node.grandparent().right:
node.color = 'b'
node.grandparent().color = 'r'
self.right_rotation(node)
self.left_rotation(node)
插入只涉及到了搜索,旋转和变色操作,因此时间复杂度为 Θ(log n) + Θ(1) + Θ(1) = Θ(log n)。
删除
红黑树的删除操作也和二叉搜索树相似,先找到删除的节点,然后根据待删除节点的孩子个数判断采取相应的删除方式。
我们知道,如果待删除的节点有两个孩子节点,我们需要从它的左子树中找到最大的节点,或者从它的右子树中找到最小的节点,交换两者的值,然后再删除交换后的节点。因此,删除拥有两个孩子的节点实际上等同于删除叶子节点或只有一个孩子的节点。
def get_max(self, root):
if root.right:
return self.get_max(root.right)
def remove(self, value):
# 树的根节点为空就抛出异常
if not self.root:
raise ValueError("The tree is null")
self.remove_node(self.root, value)
def remove_node(self, root, value):
if root is self.NIL:
return
# 搜索
if value < root.value:
self.remove_node(root.left, value)
elif value > root.value:
self.remove_node(root.right, value)
else:
# 左右孩子为空
if root.left is self.NIL and root.right is self.NIL:
self.remove_leaf(root, True)
# 只有左孩子或右孩子
elif root.left is self.NIL or root.right is self.NIL:
self.remove_one_child(root)
# 左右孩子都有
else:
temp = self.get_max(root.left) # 从左子树中找最大的节点
root.value = temp.value
self.remove_node(root.left, temp.value)
删除只有一个孩子的节点
我们先来看看删除只有一个孩子的节点。如图所示,如果删除的是黑色节点 D,我们只需要将父节点 P 和待删除节点 D 的左(右)孩子相互连接起来即可。因为删除的是黑色节点,所以从父节点 P 出发到左侧任意叶子节点所经过的黑色节点的数目一定不等于到右侧任意叶子节点所经过的黑色节点的数目,也就是说删除后违反了性质 5。为了平衡,我们需要将待删除节点 D 的左(右)孩子的颜色调整为黑色。
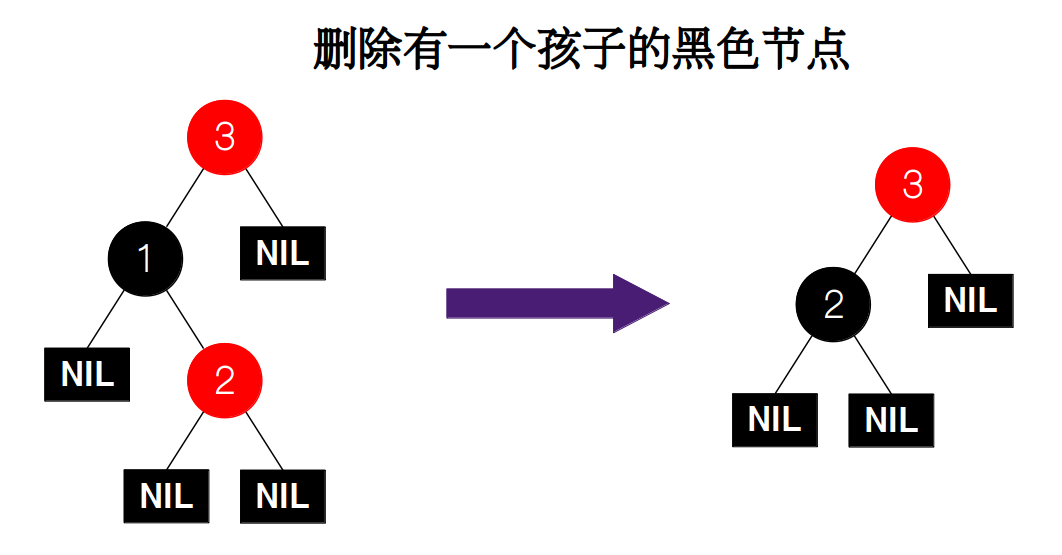
删除的节点不可能为红色节点,因为违反了性质 5。如图所示,如果就从该红色节点出发,到达左子树的任意节点所经过的黑色节点的数目一定大于 1,而它的右侧仅为一个 NIL 节点,所以经过黑色节点的数目为 1,所以我们不需要考虑删除红色节点的情况。

用代码来实现这个过程是这样子的。
def remove_one_child(self, node):
if node.left is not self.NIL:
node.left.color = 'b'
self.fix(node, node.left)
else:
node.right.color = 'b'
self.fix(node, node.right)
最后将待删除的节点删除掉,并用fix函数改变父节点和孩子节点的指针。
def fix(self, p, n):
# p.parent 为空
if not p.parent:
self.root = n
elif p.parent.left is p:
p.parent.left = n
elif p.parent.right is p:
p.parent.right = n
if n is not self.NIL and n is not None:
n.parent = p.parent
del p
删除叶子节点
下面来讨论一下删除叶子节点的情况,如果删除的是红色节点,由于删除后没有违反红黑树的任何性质,因此我们直接删除即可。
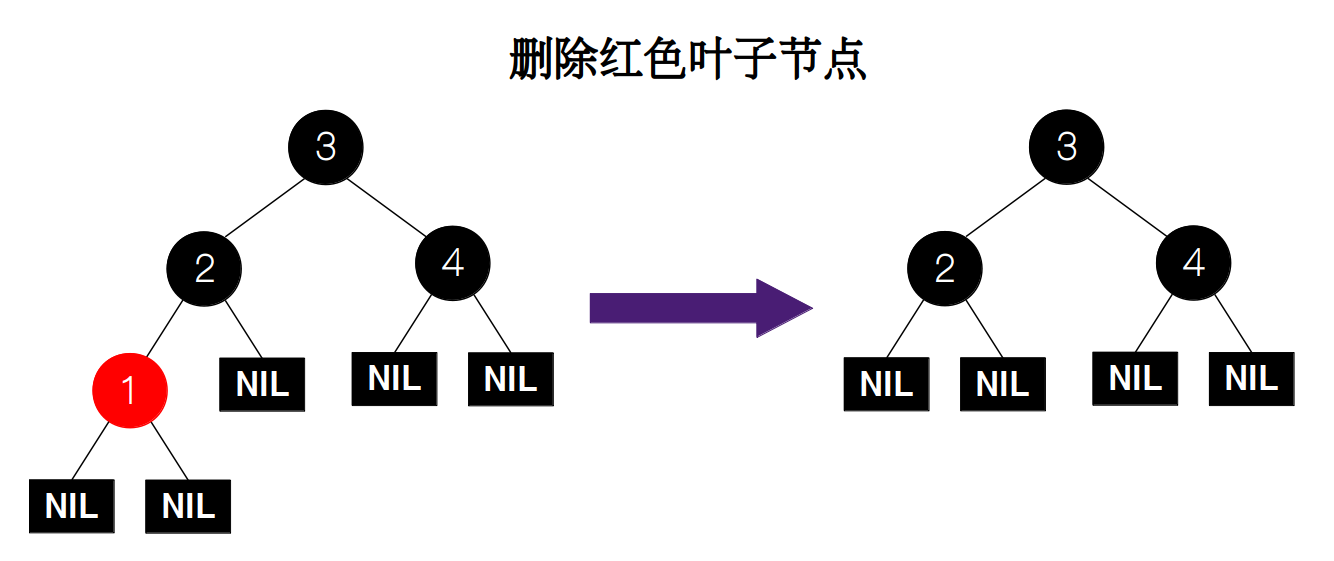
接下来是最最麻烦的删除黑色叶子节点的情况。前面看晕了的小伙伴可以先喘口气,下面的情况会更复杂。我们一共把删除黑色叶子节点分为 5 种情况。
情况 1:删除的节点为根节点。
这种情况最简单,直接删除即可,然后将红黑树的根节点
self.root置为None。![情况 1]()
情况 2:待删除节点 D 的兄弟节点 B 为红色。按照惯例,由于待删除节点 D 可以为父节点 P 的左孩子,也可以为右孩子。所以我们又可以分为两种情况。
i) D 为左孩子的情况。调整的做法是先交换父节点 P 的和兄弟节点 B 的颜色,然后对兄弟节点执行一次左旋操作。
![情况 2A]()
ii) D 为右孩子的情况。调整的做法还是先交换父节点 P 的和兄弟节点 B 的颜色,只是对兄弟节点的旋转操作变为了右旋。
![情况 2B]()
调整后,待删除的节点 D 的兄弟节点 L 的颜色为黑色,所以这就变为了后面要讨论的情况。
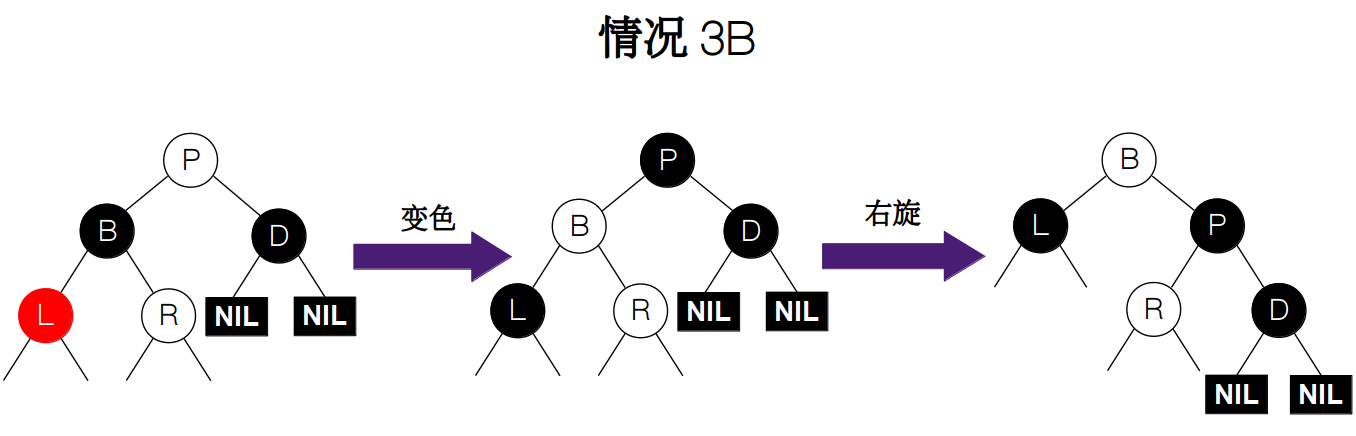
情况 3:待删除节点 D 的兄弟节点 B 为黑色,且远侄子节点为红色,这里的远侄子节点指的是离 D 较远的节点。同样,待删除节点 D 可能是根节点 P 的左(右)孩子,我们还是把它们分为两种情况:
i) D 为左孩子的情况,远侄子节点为图中的 R,图中的白色父节点 P 表示可以为任意颜色。调整策略是交换父节点 P 和兄弟节点 B 的颜色,并将远侄子节点 R 的颜色改为黑色,最后再对 B 执行一次左旋操作。
![情况 3A]()
ii) D 为右孩子的情况,远侄子节点为图中的 L。调整策略还是先交换父节点 P 和兄弟节点 B 的颜色,将远侄子节点 L 的颜色变为黑色,最后对 B 执行一次右旋操作。
![情况 3B]()
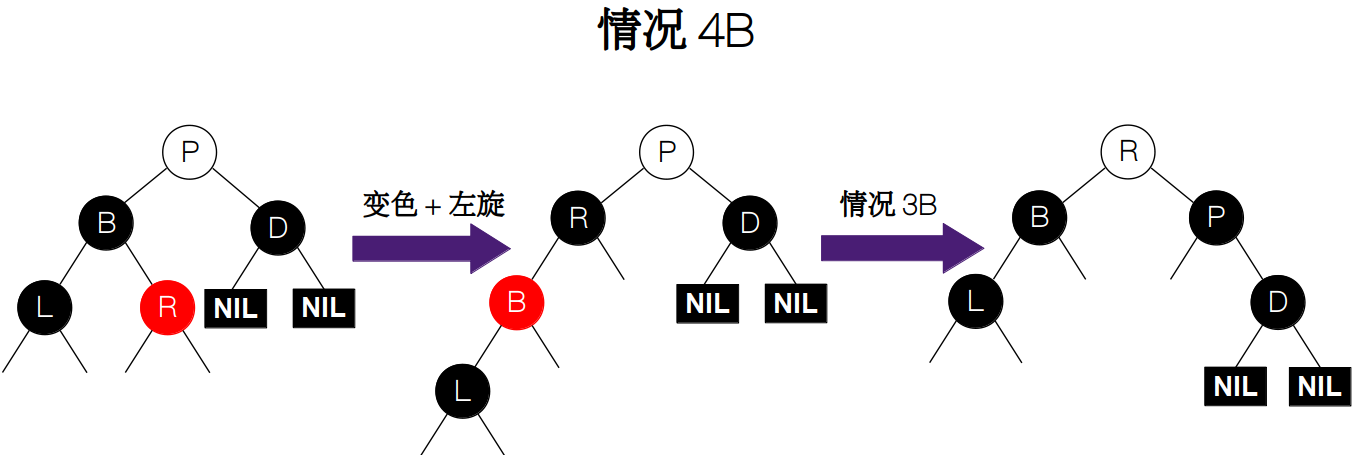
情况 4:待删除节点 D 的兄弟节点 B 为黑色,且近侄子节点为红色。相反,近侄子节点指的是离 D 较近的节点。因为待删除节点 D 依然可能是根节点 P 的左(右)孩子,所以我们还是分为两种情况:
i) D 为左孩子的情况,近侄子节点为图中的 L,图中的白色父节点 P 表示可以为任意颜色。调整方案是先交换兄弟节点 B 和近侄子节点 L 的颜色,然后对 B 执行一次右旋操作,旋转后我们发现情况变为了 3A,因此再调用一次 3A 的操作方法即可。
![情况 4A]()
ii) D 为右孩子的情况,近侄子节点为图中的 R。调整方案是先交换兄弟节点 B 和近侄子节点 R 的颜色,然后对 B 执行一次左旋操作,旋转后我们发现情况变为了 3B,因此再调用一次 3B 的操作方法即可。
![情况 4B]()
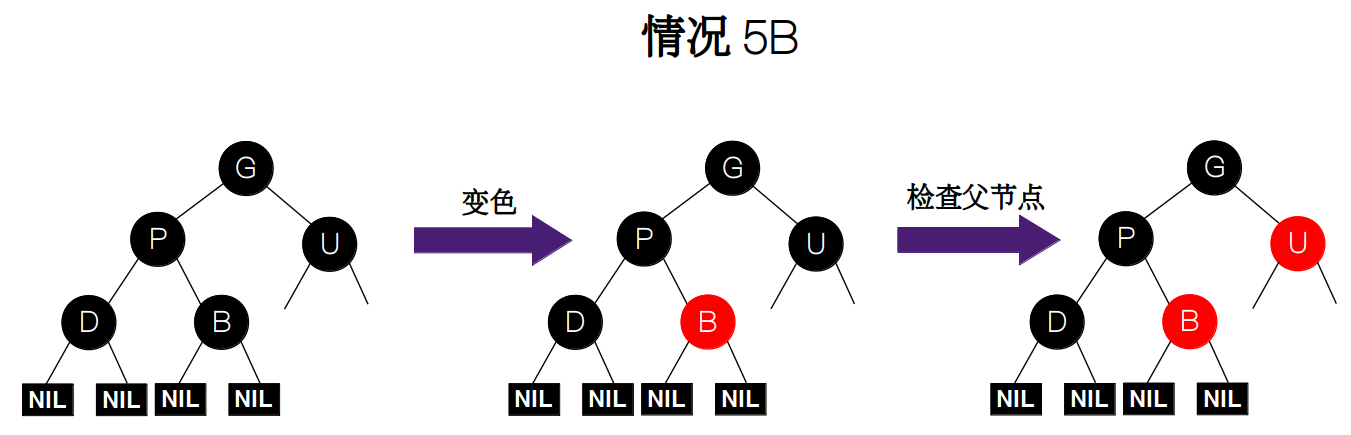
情况 5:兄弟节点 P 为红色,且它的左右孩子都为黑色。我们根据兄弟节点的颜色进一步分为两种情况。
i) 父节点 B 为红色,我们只需要交换 P 和 B 的颜色即可。
![情况 5A]()
ii) 父节点 B 为黑色,这种情况下,我们需要将 B 的颜色改为红色,由于我们不能判断父节点 P 的父节点和兄弟节点是否都为黑色,所以我们需要在父节点 P 上递归地对情况 5 的进行检查,只是我们不再删除这里的父节点了,像这样一直往上递归,直到到达根节点。
![情况 5B]()
将上述的情况全部打包成一个函数remove_leaf。
def remove_leaf(self, node, flag):
# 删除红色节点不做任何变化
if node.color == 'r':
self.fix(node, self.NIL)
return
# 为黑色节点
# 情况 1: 删除的节点为根节点
if node is self.root:
if flag:
self.fix(node, None)
return
else:
parent = node.parent
brother = node.brother()
# 情况 2: 兄弟节点为红色
if brother.color == 'r':
parent.color = 'r'; brother.color = 'b'
# 情况 2A: 待删除节点为父节点的左孩子
if node.parent.left is node:
self.left_rotation(brother)
# 情况 2B: 待删除节点为父节点的右孩子
else:
self.right_rotation(brother)
self.remove_leaf(node, True)
else:
nephew_left = brother.left
nephew_right = brother.right
# 情况 3A: 兄弟节点为黑色,右侄子节点为红色,待删除节点为父节点的左孩子
if node.parent.left is node and nephew_right.color == 'r':
brother.color = parent.color; parent.color = 'b'; nephew_right.color = 'b'
self.left_rotation(brother)
# 情况 3B: 兄弟节点为黑色,左侄子节点为红色,待删除节点为父节点的右孩子
elif node.parent.right is node and nephew_left.color == 'r':
brother.color = parent.color; parent.color = 'b'; nephew_left.color = 'b'
self.right_rotation(brother)
# 情况 4A: 兄弟节点为黑色,左侄子节点为红色,待删除节点为父节点的左孩子
elif node.parent.left is node and nephew_left.color == 'r':
nephew_left.color = 'b'; brother.color = 'r'
self.right_rotation(nephew_left)
self.remove_leaf(node, True)
# 情况 4B: 兄弟节点为黑色,右侄子节点为红色,待删除节点为父节点的右孩子
elif node.parent.right is node and nephew_right.color == 'r':
nephew_right.color = 'b'; brother.color = 'r'
self.left_rotation(nephew_right)
self.remove_leaf(node, True)
# 情况 5: 兄弟节点为黑色,并且两个孩子都为黑色节点
elif brother.left.color == 'b' and brother.right.color == 'b':
# 情况 5A: 父节点为红色
if parent.color == 'r':
parent.color = 'b'; brother.color = 'r'
# 情况 5B: 父节点为黑色
else:
brother.color = 'r'
self.remove_leaf(parent, False)
# 决定是否删除节点,flag 为 False 时实用于情况 5B
if flag:
self.fix(node, self.NIL)
删除操作也包含了搜索,旋转和变色操作,因此时间复杂度也为 Θ(log n) + Θ(1) + Θ(1) = Θ(log n)。
例子
让我们来看一个具体的例子,假设从数组[1, 3, 4, 2, 5, 7, 6]构建红黑树。
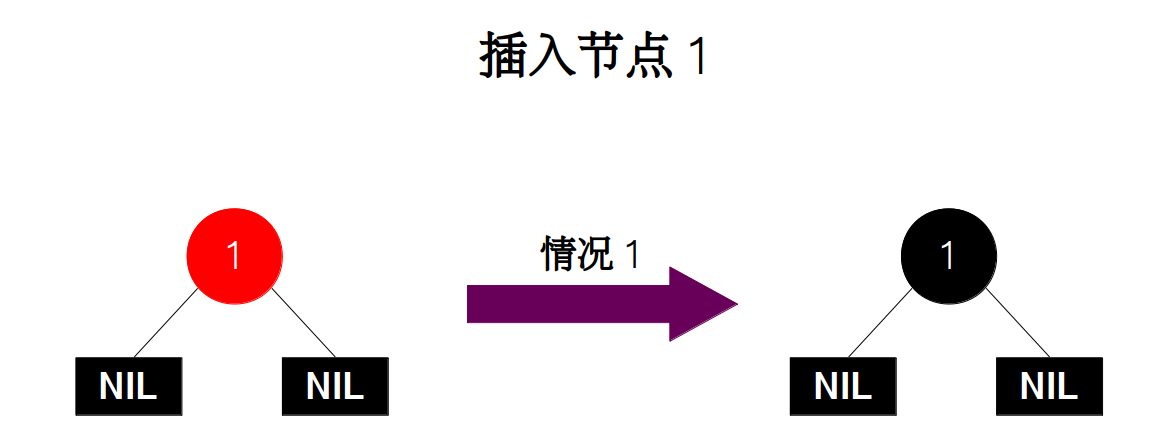
插入节点 1。由于是根节点,所以需要将颜色置为黑色。
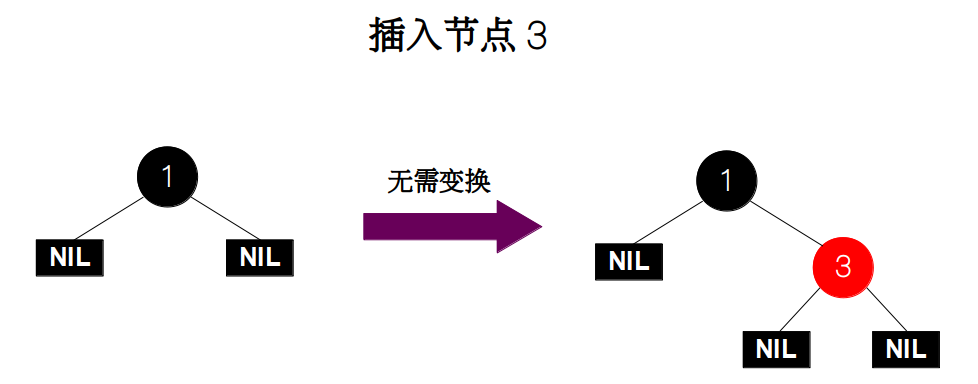
插入节点 3。没有违反任何性质,不做任何改变。
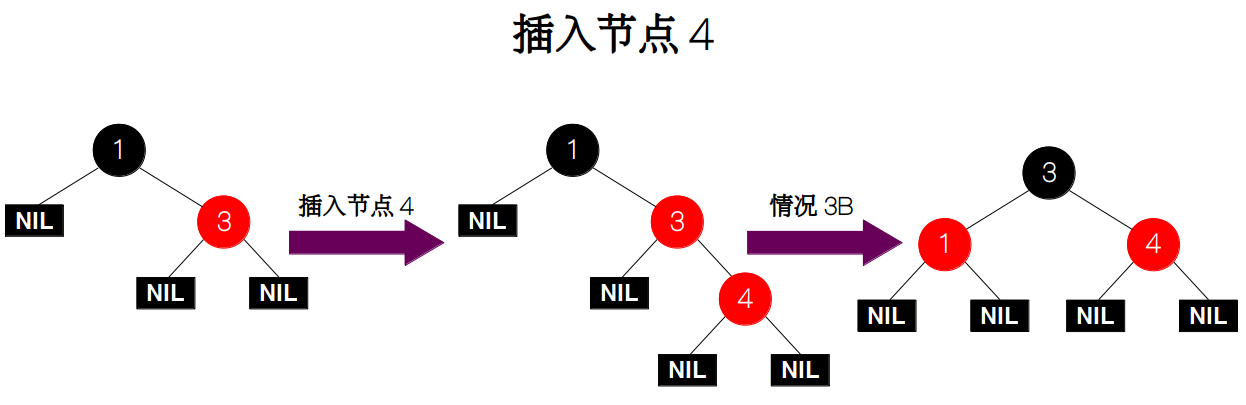
插入节点 4。因为叔父节点为 NIL,祖父节点的右孩子为父节点,父节点的右孩子为新插入节点,为情况 3B。因此我们需要先交换父节点 3 和 其祖父节点 1 的颜色,最后再对节点 3 进行左旋。
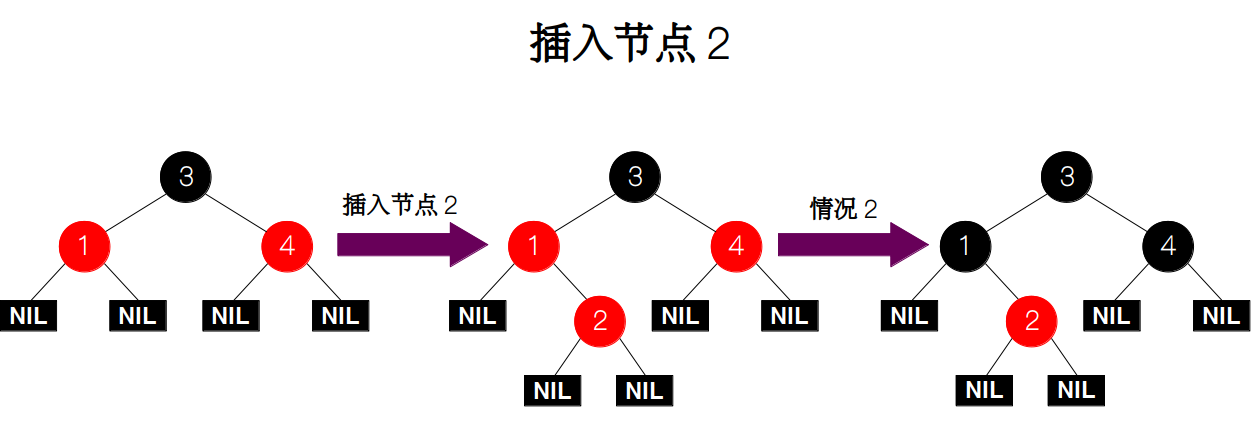
插入节点 2。其祖父节点为黑色,父节点和叔父节点均为红色,情况 2 满足。所以我们将祖父节点的颜色变为红色,将父节点和叔父节点变为黑色,然后递归地对祖父节点进行检查,发现祖父节点为树的根节点,且为红色,因此满足情况 1,故将颜色变为黑色。
插入节点 5。没有违反任何性质,不做任何改变。
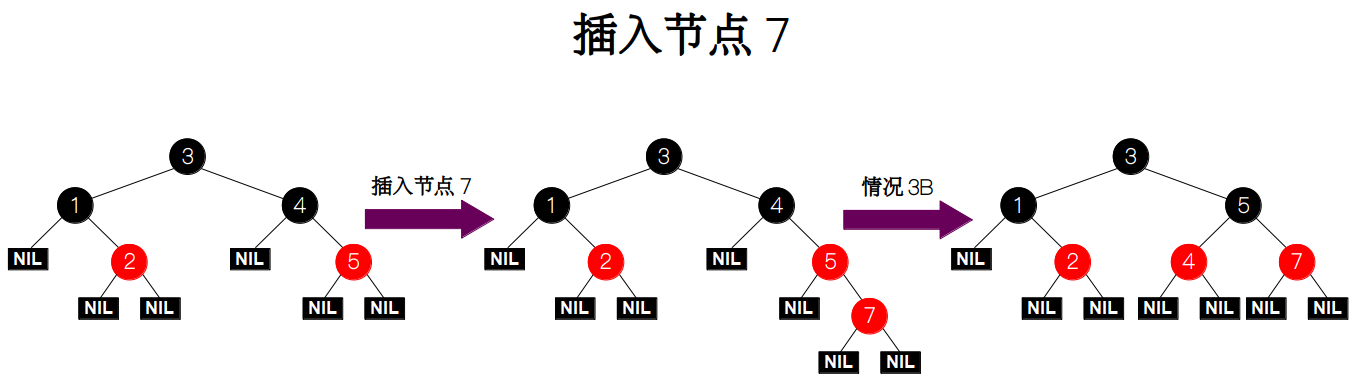
插入节点 7。因为叔父节点为黑色,祖父节点的右孩子为父节点,父节点的右孩子为新插入节点,也为情况 3B。因此我们需要先交换父节点 5 和 其祖父节点 4 的颜色,最后再对节点 5 进行左旋。
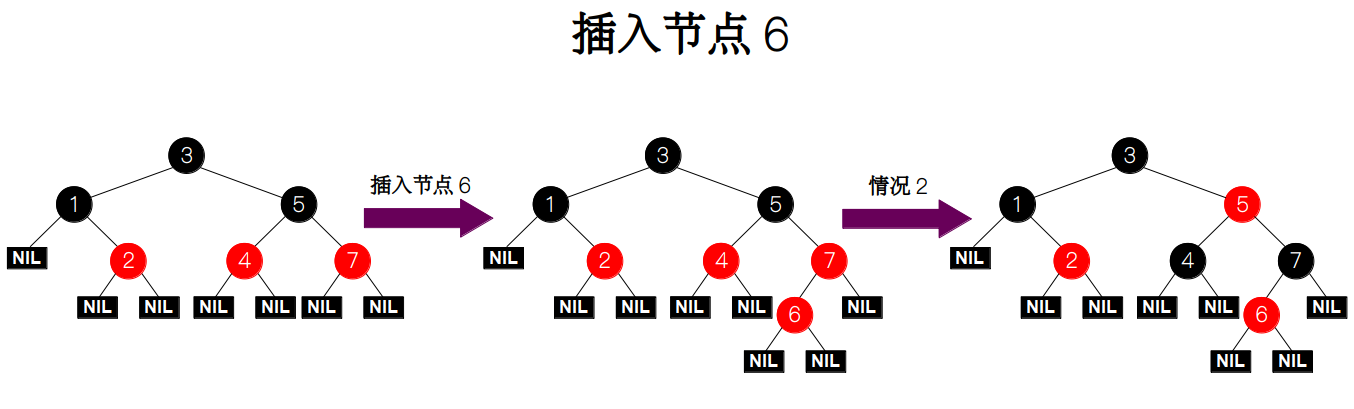
最后插入节点 6。发现也满足情况 2,所以需要将祖父节点的颜色变为红色,将父节点和叔父节点变为黑色,然后递归地对祖父节点进行检查,最终得到的红黑树如下图所示。
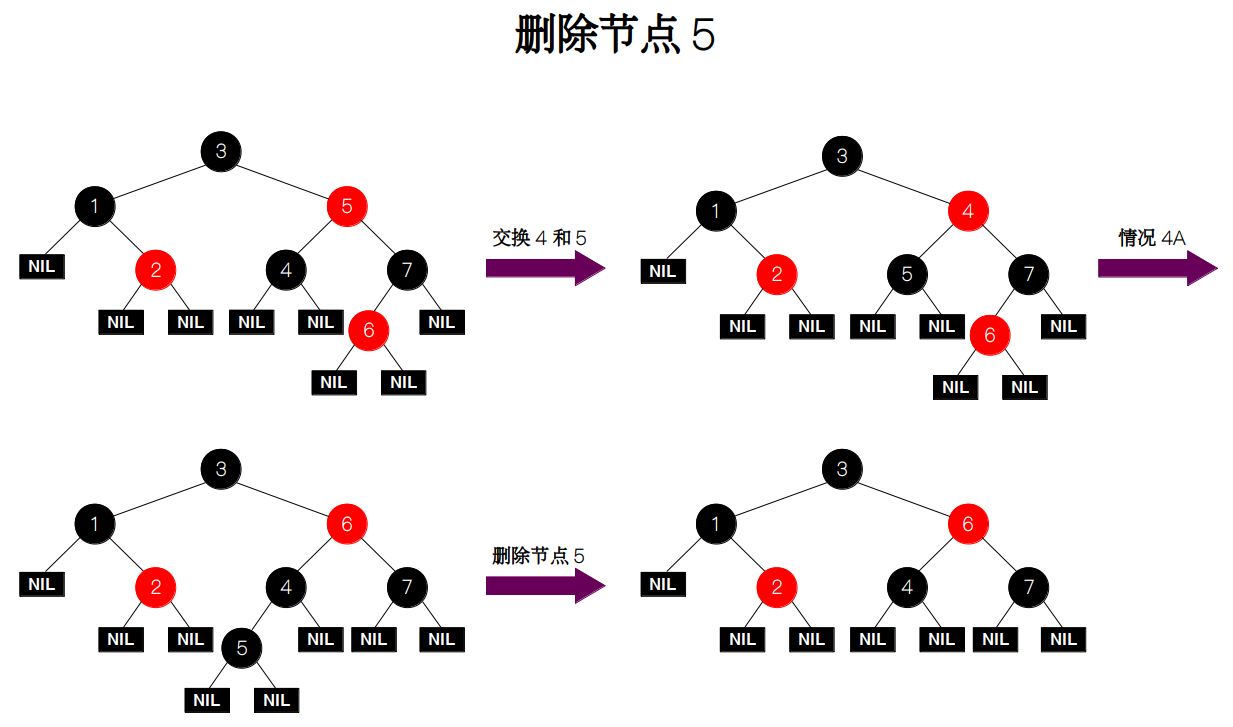
然后我们在从这棵红黑树中依次删除 5, 1, 7。
删除节点 5。节点 5 有两个孩子节点,所以需要在它的左子树中找到最大的节点(节点 4),然后交换两者的值,这样就等同于删除一个黑色的叶子节点。我们发现它的兄弟节点为黑色,左侄子节点为红色,待删除节点为父节点的左孩子,所以满足情况 4A。做出调整是先交换兄弟节点 7 和近侄子节点 6 的颜色,然后对节点 6 执行一次右旋,再次检查待删除节点,发现又满足条件 3A,所以先交换父节点 4 和兄弟节点 6 的颜色,并将远侄子节点 7 的颜色变为黑色,最后再对节点 6 执行一次左旋操作。
删除节点 1。由于只有一个孩子节点,因此只需要将节点 1 的右节点 2 与父节点 3 连接起来,然后将节点 2 的颜色变为黑色即可。
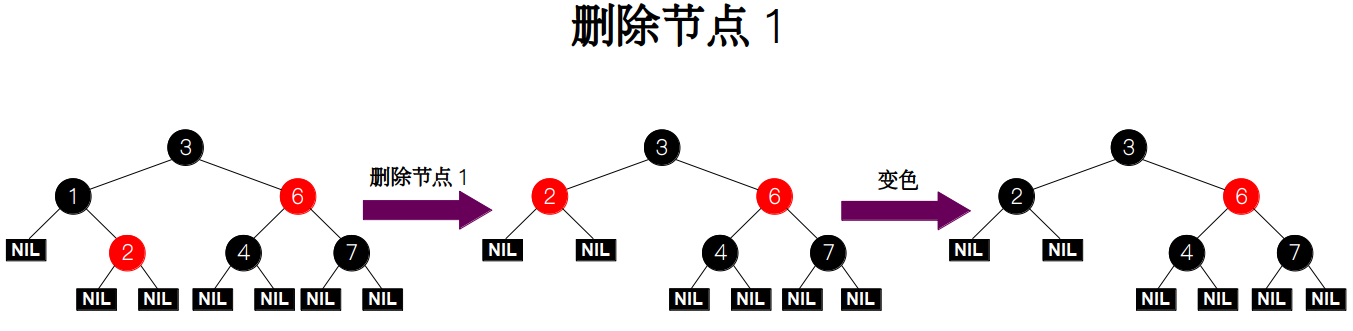
删除节点 7。节点 7 为黑色叶子节点,且兄弟节点 4 为黑色,父节点 6 为红色,故满足条件 5A。因此我们只需要交换父节点和兄弟节点的颜色即可。
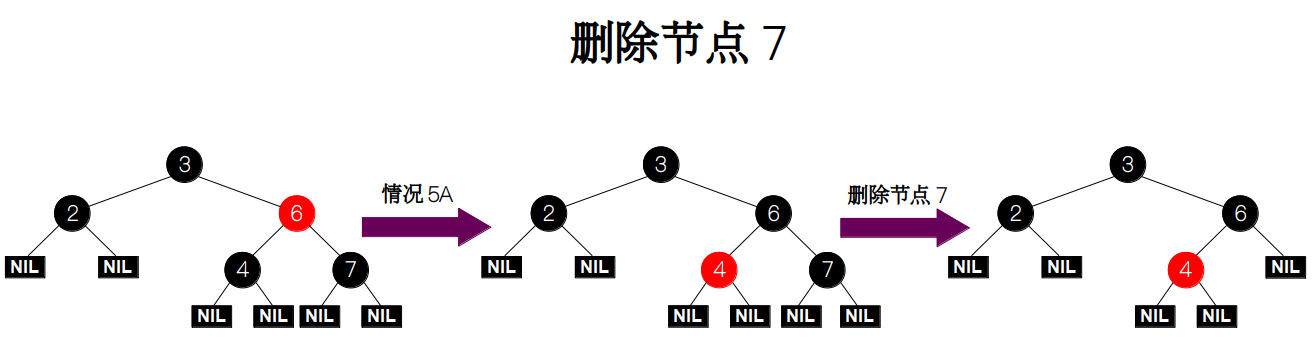
这样我们就讲完了一个完整例子了。红黑树的操作十分复杂,情况非常多,代码也非常难理解,所以需要大家多花点时间消化本节的内容啊~
演示
如果你觉得上面的代码很难理解,不妨去这个可视化网站,里面有各种数据结构和算法的可视化,可以帮助我们很好地理解那些复杂的数据结构。
→ 本节全部代码 ←