介绍
前面我们学习了回溯法,它的主要思想是不停地探索状态空间,如果遇到不满足条件的解就停止探索,然后回溯到上一个状态,再探索其他的状态,直到探索到问题的解。
回溯的方法的确是一种可行的办法,但是它只能求解像 n-皇后,集合问题这样的非优化问题,一旦涉及到优化问题它就束手无策了。因为回溯的过程只会发生在探索过程中不满足限制条件时发生,所以用回溯法求解的问题一般都有多个解,但对于最优问题(分配问题、背包问题等)来讲,满足限制条件的解有很多,我们要做的是从所有满足条件的解中找到最好的那一个,所以我们就有了分支限界(branch and bound)这种方式来帮助我们解决这一类问题。
如何解决
在解决最优问题的时候,我们还是需要构建一棵状态空间树,只是和回溯不同的是,回溯是基于广度优先的方式来扩展空间树中的节点的,而分支限界法是基于深度优先的方式来扩展节点的,也就是说,分支界定法是每次构建出解空间树中一层的全部节点。那么具体该怎么做呢?我们要明白的是,任何一个最优问题都存在一个上界或下界,也就是说,对于求解像最低开销,最短路径这类问题时,一定存在一个下界使得最后问题的解不会低于这个值。相反,如果问题是求解最大收益,那么一定会有一个上界来约束最终的解。
在具体求解的过程中,每探索出一个新的节点(进入新的状态),我们就要计算当前情况下的上界或下界,然后在状态转移(探索下一层节点)的时候选择上界最大或下界最小的节点,这样我们才会更逼近最大或最小值,这样听起来太挺抽象了,我们还是来看一个具体的例子吧。
分配问题
回顾一下我们前面所学过的内容,分配问题的问题描述为将 n 件任务分配给 n 名员工,一名员工只能完成一件任务,每名员工做每个任务都有对应的时间开销,我们要优化的问题是怎样使总开销最小。
拿一个具体的实例来看,假设有 4 名员工,每名员工做每件任务的时间如下图的表格所示。
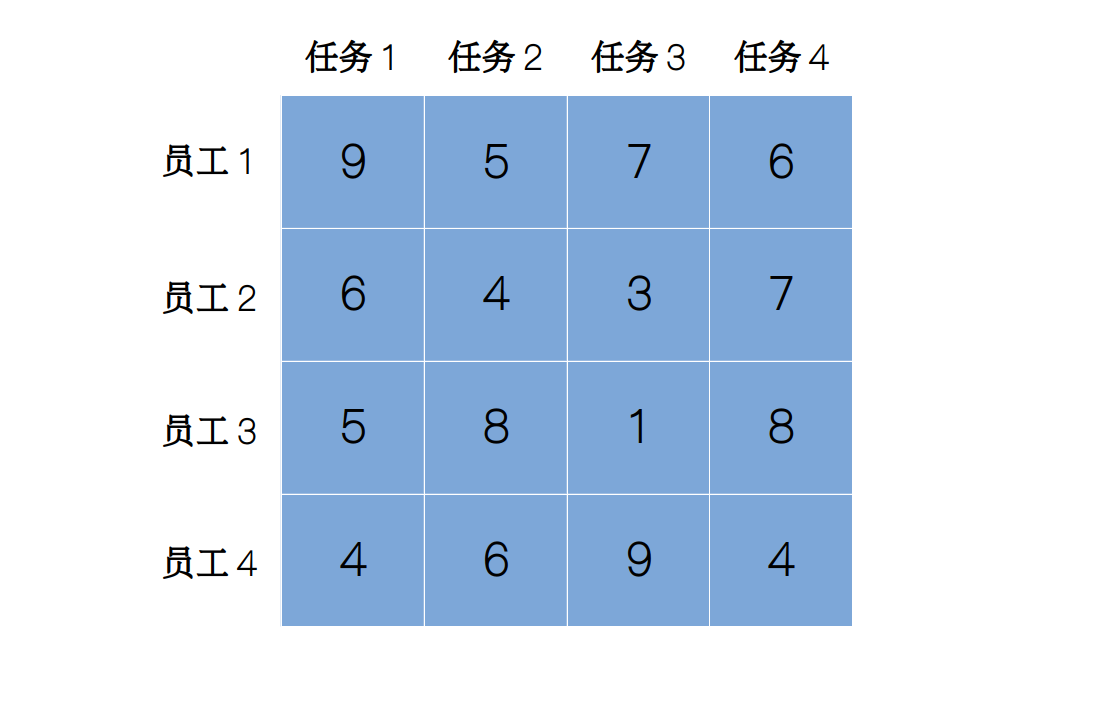
由于我们要使总开销最小,所以一定存在一个下界,要怎样来定这个下界呢?最简单的方法就是从每一行选出一个最小值,然后将它们相加。对于上面的表格来讲,下界就为 13,表示这个问题的总开销不可能小于 13。

于是,我们将这个状态作为我们的初始状态(initial state)。
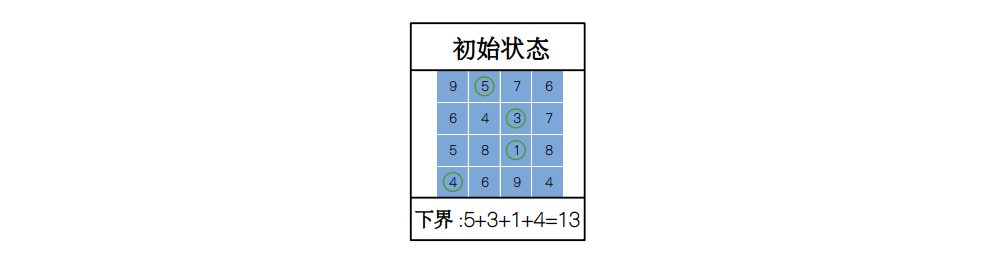
接下来,我们构建出下一层状态节点,然后依次计算出该状态下的下界,在这里,我们要做的是依次选择第一行里的元素,然后把对应行和列全部划掉,然后从剩下的元素中计算下界,比如说这里如果我们选择第一行的 7,划去第一行和第三列后,从剩余的 3 × 3 的表中每一行中选择最小值,然后相加得到下界为 20(包含 7),表示如果第一名员工选择任务 3,总开销不会小于 20。于是我们将第一行的元素对应的所有下界通通用这种方式求出来,然后在状态空间树中生成相应的节点。
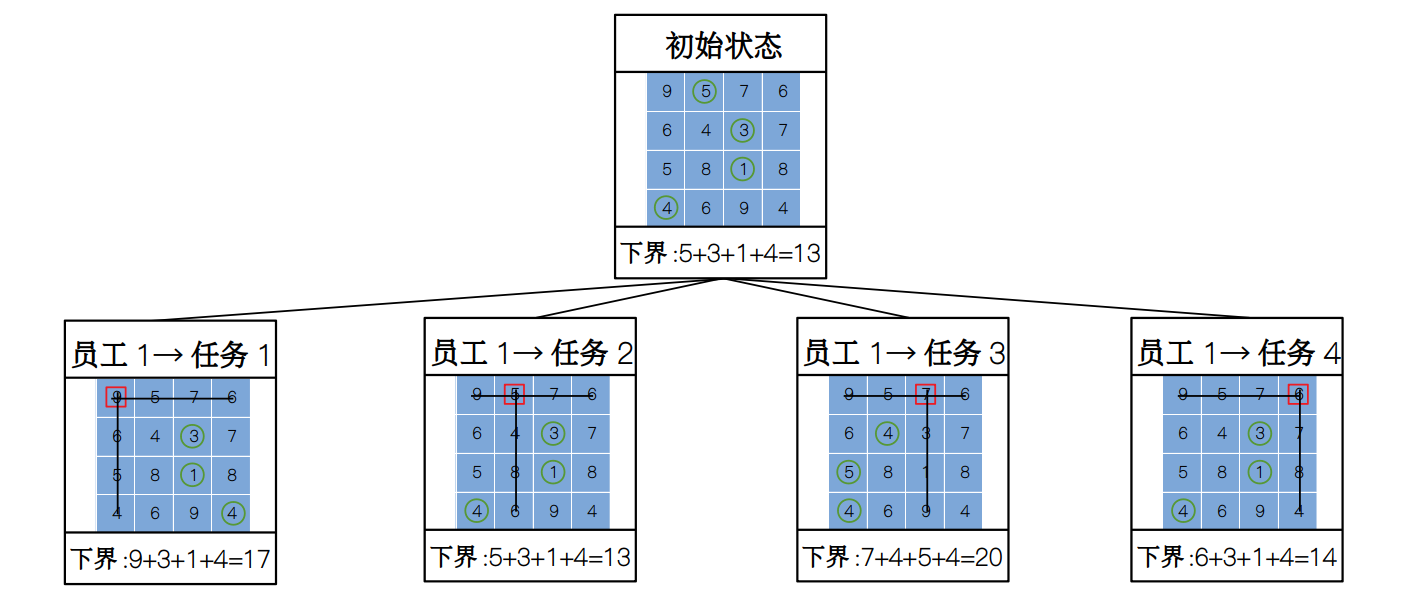
构建完第一层的节点之后,我们发现,第一名员工选择任务 2 的下界最小,即潜在的解为最小。因此,我们从这个节点出发,继续向下搜索,分别计算出第二名员工选择剩下 3 件任务时的下界,得到的状态空间树如下图所示:
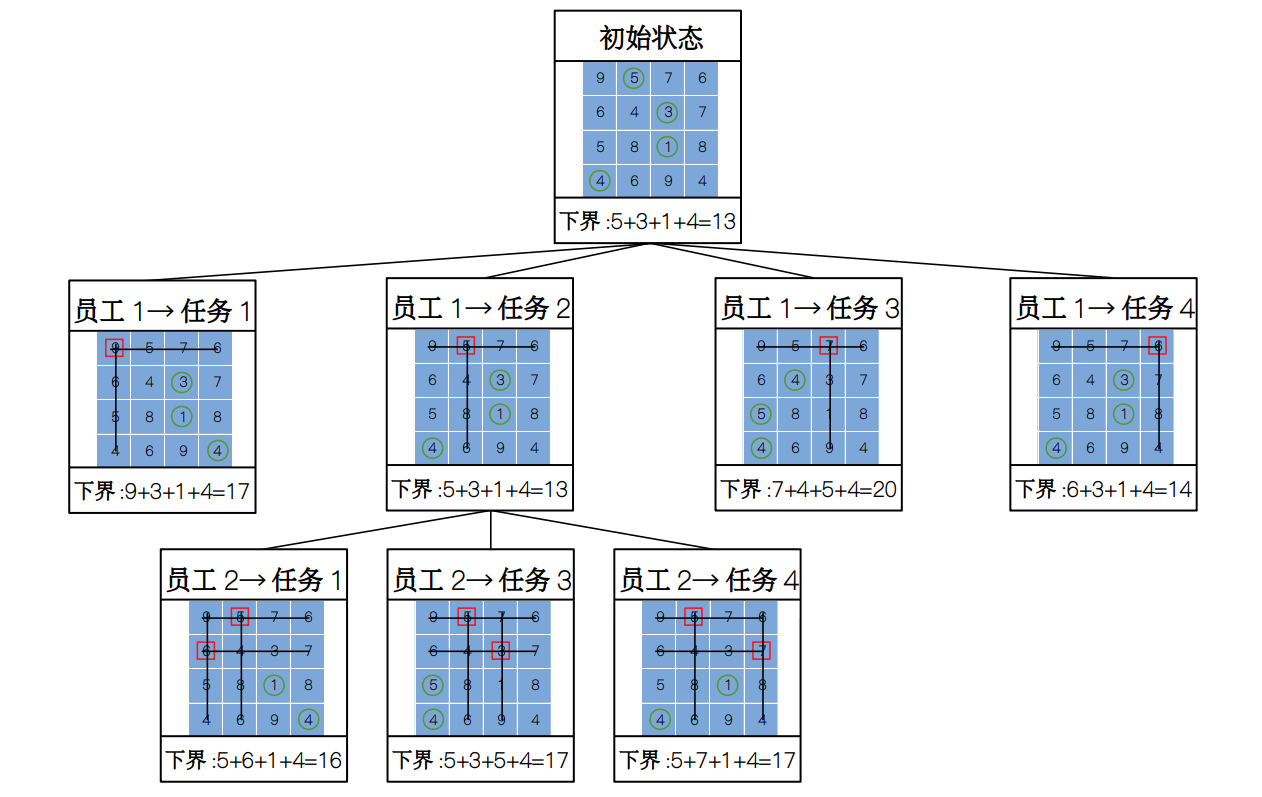
观察得到,无论第二名选择哪一件任务,它们对应的下界都要大于第一名员工选择任务 4 时的下界,所以这里我们就不能再从第二名员工那里继续往下搜索了。因为存在更小的潜在解,所以我们要退回到第一行,让员工 1 选择任务 4,然后从这个状态出发继续往下搜索。于是状态树变为:
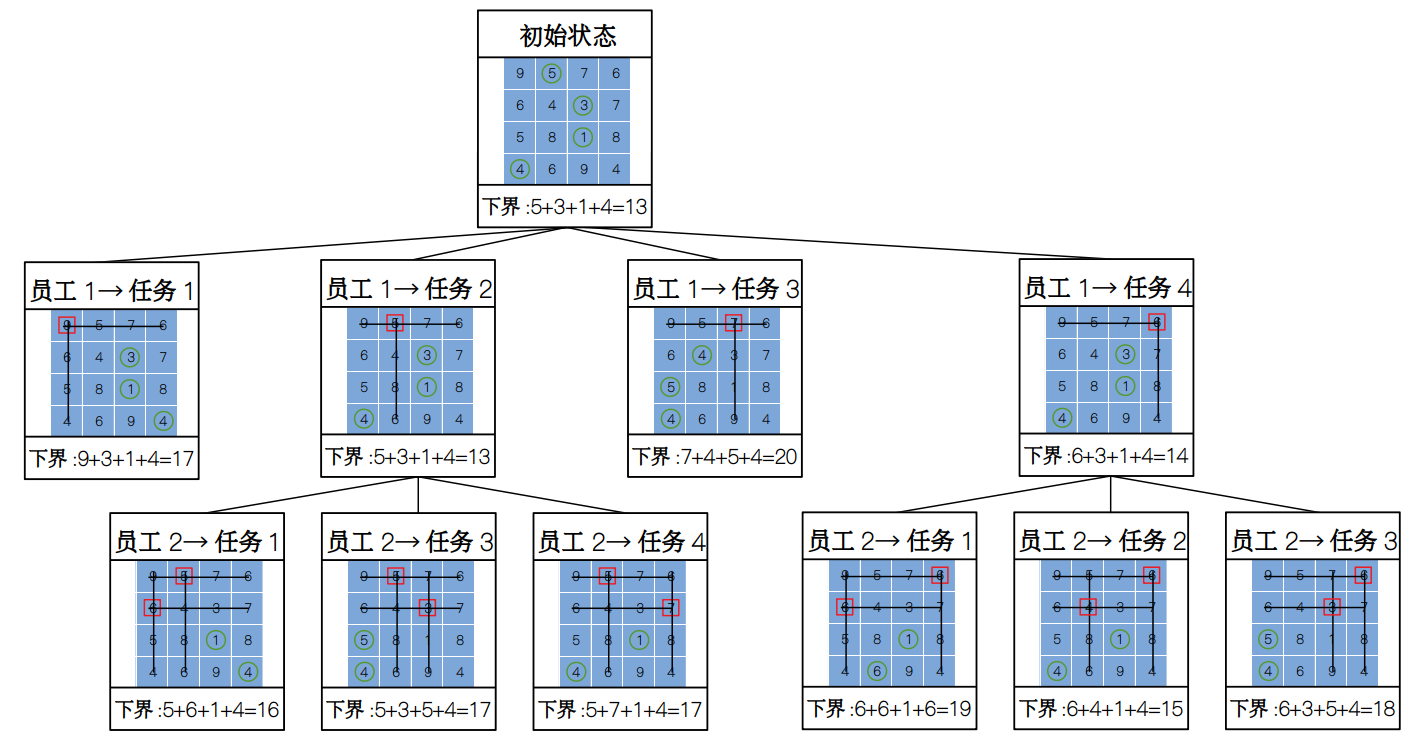
这时,我们看到如果选择第二行的第二列,所对应的下界为全局的最小,因此我们便可以继续往下搜索啦,于是构建出最后一层的状态空间树。
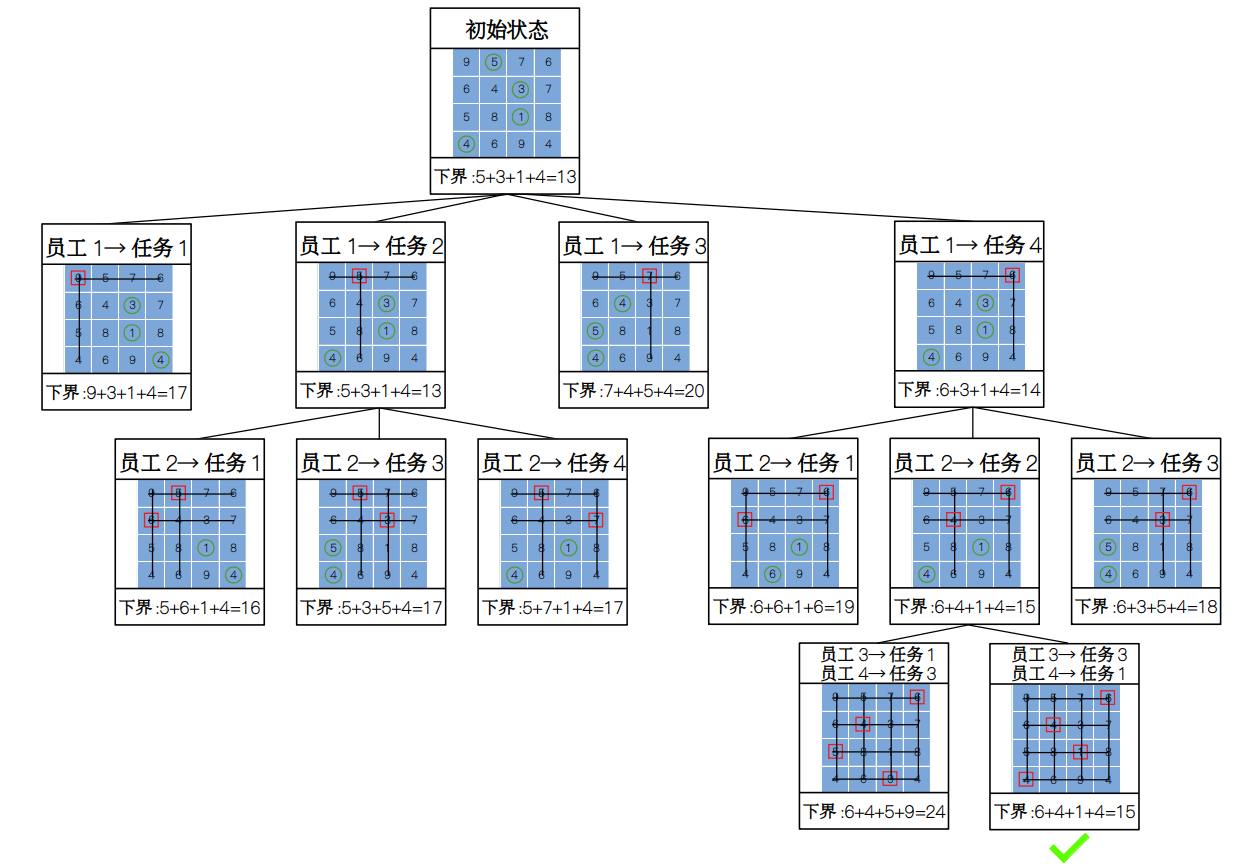
搜索到最后一层的时候,如果发现计算出的下界还是全局的最小值,我们就可以得到该下界就为分配问题的解了。在上面的例子中,最短时间开销就为 15。
实现
代码的实现分为几个部分,为了实现方便,这里用到了numpy。
import numpy as np
对于每一个状态,我们用一个类State来表示。
class State(object):
def __init__(self, matrix, lb, row, process):
self.matrix = matrix # 当前状态下的表格
self.lb = lb # 下界
self.process = process # 已处理行的累积值
self.row = row # 当前行
compute_lower_bound用于计算当前状态下的下界。
def compute_lower_bound(a):
return np.sum(np.min(a, axis=1))
因为每次在状态转移的过程中需要从所有的状态中选择最小的下界,而构建新的节点的时候又需要添加新的状态,所以这里用堆来作为我们的数据结构就再合适不过了。下面是调整堆结构的两个函数fix_up和fix_down。
def fix_up(queue):
temp_idx = len(queue) - 1
parent_idx = (temp_idx - 1) // 2
heap = False
while not heap and parent_idx >= 0:
# 判断是否满足堆的性质
if queue[temp_idx].lb < queue[parent_idx].lb:
queue[temp_idx], queue[parent_idx] = queue[parent_idx], queue[temp_idx]
else:
heap = True
# 更新索引值
temp_idx = parent_idx
parent_idx = (temp_idx - 1) // 2
def fix_down(queue):
if not queue:
return
temp_idx = 0; size = len(queue)
temp_ver = queue[temp_idx] # 暂存当前节点
heap = False
while not heap and 2 * temp_idx + 1 < size:
j = 2 * temp_idx + 1 # 左孩子的索引
# 右孩子存在
if j < size - 1:
# 比较两个节点的权重
if queue[j].lb > queue[j + 1].lb:
j = j + 1
# 判断是否满足堆的性质
if queue[j].lb >= temp_ver.lb:
heap = True
else:
queue[temp_idx] = queue[j]
temp_idx = j # 更新 temp_idx
queue[temp_idx] = temp_ver
最后是我们的主函数 main。
def main(c):
row, col = c.shape # 获取表格的大小
pqueue = [] # 优先队列
cur_state = State(c, 0, 0, 0) # 初始状态
pqueue.append(cur_state)
while cur_state.row < row-1:
cur_state = pqueue.pop()
fix_down(pqueue) # 调整堆结构
cur_matrix = cur_state.matrix; cur_row = cur_state.row
for cur_col in range(col):
if cur_matrix[cur_row][cur_col] != np.inf:
temp_matrix = cur_matrix.copy()
temp_matrix[cur_row, :] = np.inf; temp_matrix[:, cur_col] = np.inf # 用 ∞ 划掉对应行和列
lower_bound = compute_lower_bound(temp_matrix[cur_row+1:]) + cur_state.process + cur_matrix[cur_row][cur_col] # 计算下界
process = cur_state.process + cur_matrix[cur_row][cur_col] # 更新已处理行的累积值
pqueue.append(State(temp_matrix, lower_bound, cur_row+1, process))
fix_up(pqueue) # 调整堆结构
pqueue[0], pqueue[-1] = pqueue[-1], pqueue[0]
return cur_state.lb
这样我们就完成用分支限界法解决分配问题的全部代码了,是不是很简单呢~
→ 本节全部代码 ←