Hexo |

贪心算法

前面我们讲到的动态规划一般解决的都是最优问题，通常情况下我们先将原问题拆分成数个子问题，然后找出这些子问题之间的关系，即怎样从规模为 n - 1 的子问题的解中得出规模为 n 的子问题的解（F(n-1) –> F(n)），最后从最小子问题入手，用迭代的方式求出原问题的解。这样虽然每次都能求出最优解，并且这里的最优是全局最优，但是动态规划的方法过于复杂，难以理解，而且需要额外的内存空间来储存子问题的解。在一些只需要近似最优解的场景中，动态规划未免显得有点头重脚轻了。因此，我们就有了贪心算法，它能帮助我们找出近似的解。

贪心算法（greedy algorithm）顾名思义就是算法采用贪心的策略，来解决一些复杂的问题。一个最简单的例子就是找零钱问题，假设有面值为 5 元，2 元，1 元的钱币，怎样凑出金额为 6 元的零钱，使得用到的钱币数最少，用动态规划的方法来计算的话，我们得到最少需要 2 枚钱币（5 元和 1 元）。但是如果我们采用贪心算法的策略，每次选择钱币金额最大的，使子问题的规模尽可能的变小，我们同样能够得到 5 元和 1 元的组合。

那么贪心算法真的就能解决所有的最优化问题吗？我们将钱币面值稍稍做一点改动，变为 4 元，3 元和 1 元（仅仅是假设啦），找零钱的金额还是 6 元。如果采用贪心的策略，我们先选择 4 元的，然后剩下的 2 元用两个 1 元组合而成，就需要 3 枚钱币，而实际上我们只需要两个 3 元就可以凑齐 6 元。因此，贪心算法并不是在所有的情况下都能有最优解。

最小生成树

下面就来看看用贪心算法来解决具体的问题。我们从图入手，介绍两种最小生成树的算法：普林姆算法和克鲁斯卡尔算法。首先来介绍一下什么是生成树。

下图中每一个节点代表一个村庄，有一些路使这些村庄之间彼此相互连接，也就是图中的每条边，现在要将这些路拓宽，但由于受到预算的限制，不能覆盖所有的路，只能选择一部分拓宽，但要使拓宽的路将所有的村庄连通。换句话说，从任何一个村庄出发都能够到达其他的村庄。

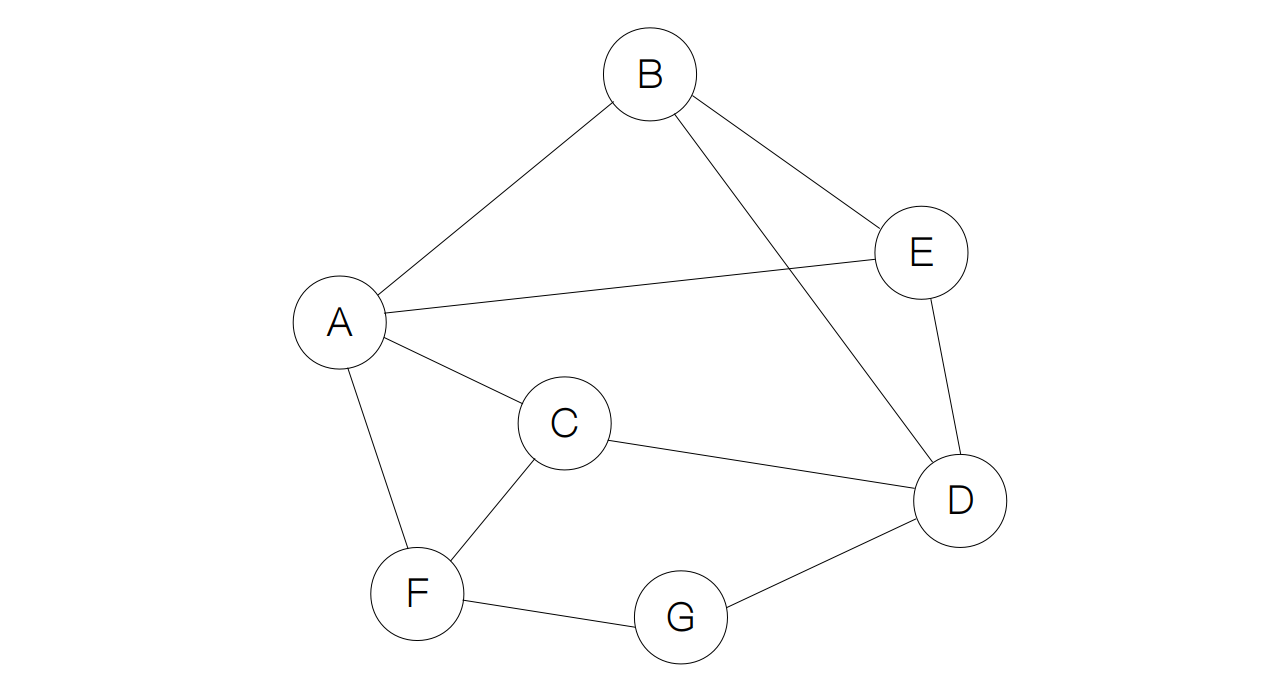
生成树就是在图中，由边的子集所构成的树，并且满足全部节点都被包括在内。在上面的例子中，我们可以画出不止一种生成树。

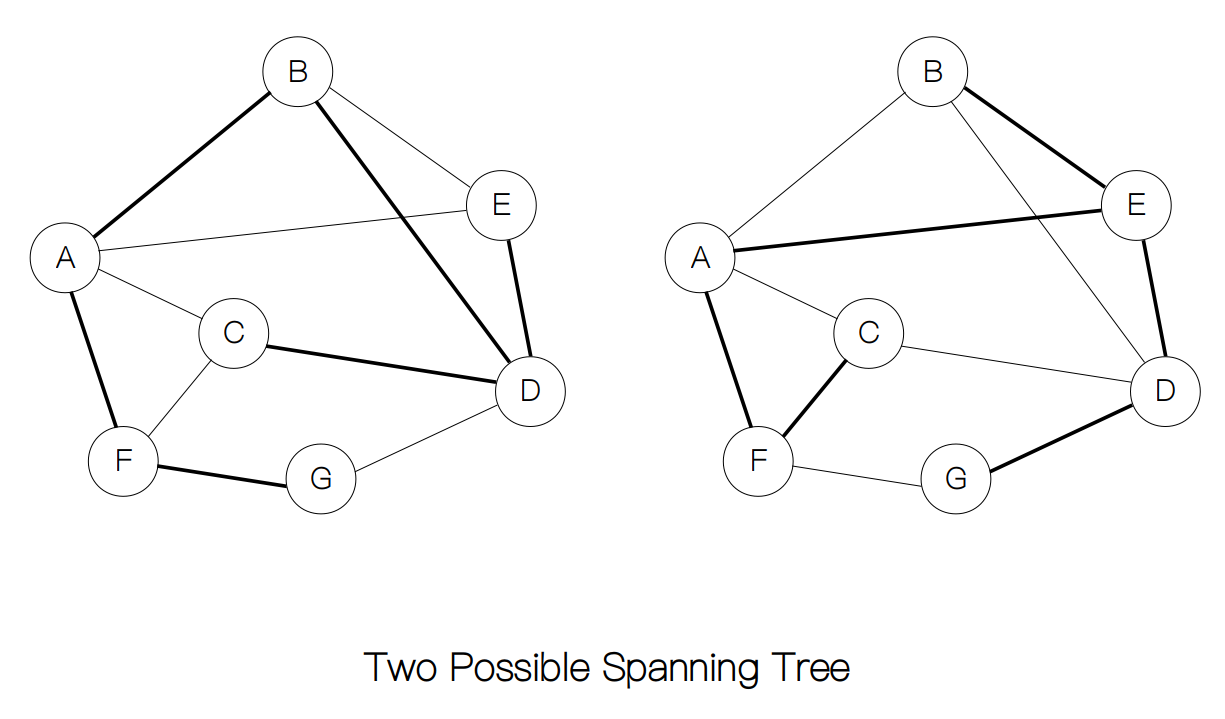
假设村庄的拓宽道路的预算被进一步地缩减，需要用最少的材料来修路，这种情况下又怎么办呢？如果村庄间的距离已知，那么只需要计算上面的生成树中每一条边的权重进行求和，选择最小的即可。

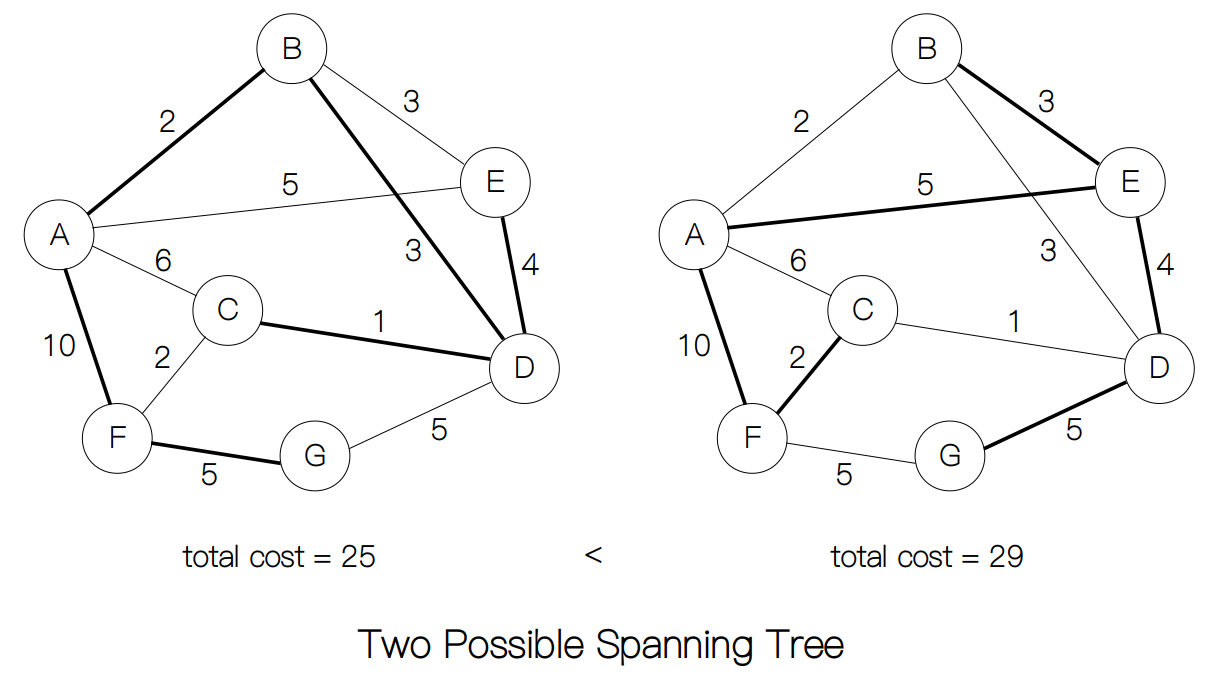
但每次都把生成树求出来，计算它们的权重的总和，然后选最小者这种方法太低效了，如果我们采用贪心策略，问题就要好办许多。

普林姆算法

根据上面的例子，我们来讲一讲普林姆算法的全过程，它正是采用的贪心策略。假设我们有图 G = <V, E>，整个过程需要用到 5 步。

第一步：初始化集合 V_visited = {}，E_weight = {} 和 E_target = {}，并从图中选择一个起始节点 x，标记为已访问，加入到集合 V_visited 。
第二步：将所有未被访问的边 (u, v) 放入到集合 E_weight 中，并标记为已访问。
第三步：从集合 E_weight 中取出最小的边 (u, v), 如果 v 为被访问，执行第三步；如果没有被访问，执行第四步。
第四步：把 v 标记为已访问，并将 v 放入到集合 V_visited 中，将边 (u, v) 放入到集合 E_target 中。
第五步：重复第三步，直到 V_visited = V。

在写出普林姆算法之前，我们先定义Vertex类和Edge类来表示节点和边：

class Vertex(object):
    def __init__(self, name):
        self.name = name
        self.neighbours = []
        self.visited = False

class Edge(object):
    def __init__(self, pre, next, weight):
        self.pre = pre
        self.next = next
        self.visited = False
        self.weight = weight

在第二步和第三步中我们发现，每次都会返回一个最小权重边，因此会用到堆来实现优先队列的过程，这样每次权重最小的边都位于堆顶。这里我们用到两个函数fix_up和fix_down来分别向上和向下调整堆的结构。

def fix_up(queue):
    temp_idx = len(queue) - 1
    parent_idx = (temp_idx - 1) // 2
    heap = False
    while not heap and parent_idx >= 0:
        # 判断是否满足堆的性质
        if queue[temp_idx].weight < queue[parent_idx].weight:
            queue[temp_idx], queue[parent_idx] = queue[parent_idx], queue[temp_idx]
        else:
            heap = True
        # 更新索引值
        temp_idx = parent_idx
        parent_idx = (temp_idx - 1) // 2
def fix_down(queue):
    temp_idx = 0; size = len(queue)
    temp_ver = queue[temp_idx]  # 暂存当前节点
    heap = False
    while not heap and 2 * temp_idx + 1 < size:
        j = 2 * temp_idx + 1  # 左孩子的索引
        # 右孩子存在
        if j < size - 1:
            # 比较两个节点的权重
            if queue[j].weight > queue[j + 1].weight:
                j = j + 1
        # 判断是否满足堆的性质
        if queue[j].weight >= temp_ver.weight:
            heap = True
        else:
            queue[temp_idx] = queue[j]
            temp_idx = j  # 更新 temp_idx
    queue[temp_idx] = temp_ver

有了堆的结构之后，我们就很容易写出主函数Prim了。

def Prim(G, source):
    V, _ = G  # 从 G 中获取节点集合和边集合
    v_set = V
    pqueue = []  # 建立优先队列
    source.visited = True; v_set.remove(source); cur = source
    total_cost = 0
    while v_set:
        for e in cur.neighbours:
            if not e.visited:
                e.visited = True
                pqueue.append(e)  # 将 e 加入到堆
                fix_up(pqueue)
        pqueue[0], pqueue[-1] = pqueue[-1], pqueue[0]
        temp = pqueue.pop()  # 删除堆顶元素
        fix_down(pqueue)
        if not temp.pre.visited:
            cur = temp.pre
        elif not temp.next.visited:
            cur = temp.next
        else:
            continue  # 下一个节点已被访问
        cur.visited = True
        print(temp.pre.name + '--' + temp.next.name)
        total_cost += temp.weight
        v_set.remove(cur)
    return total_cost

我们用一张动图来表示普林姆算法的整个过程。

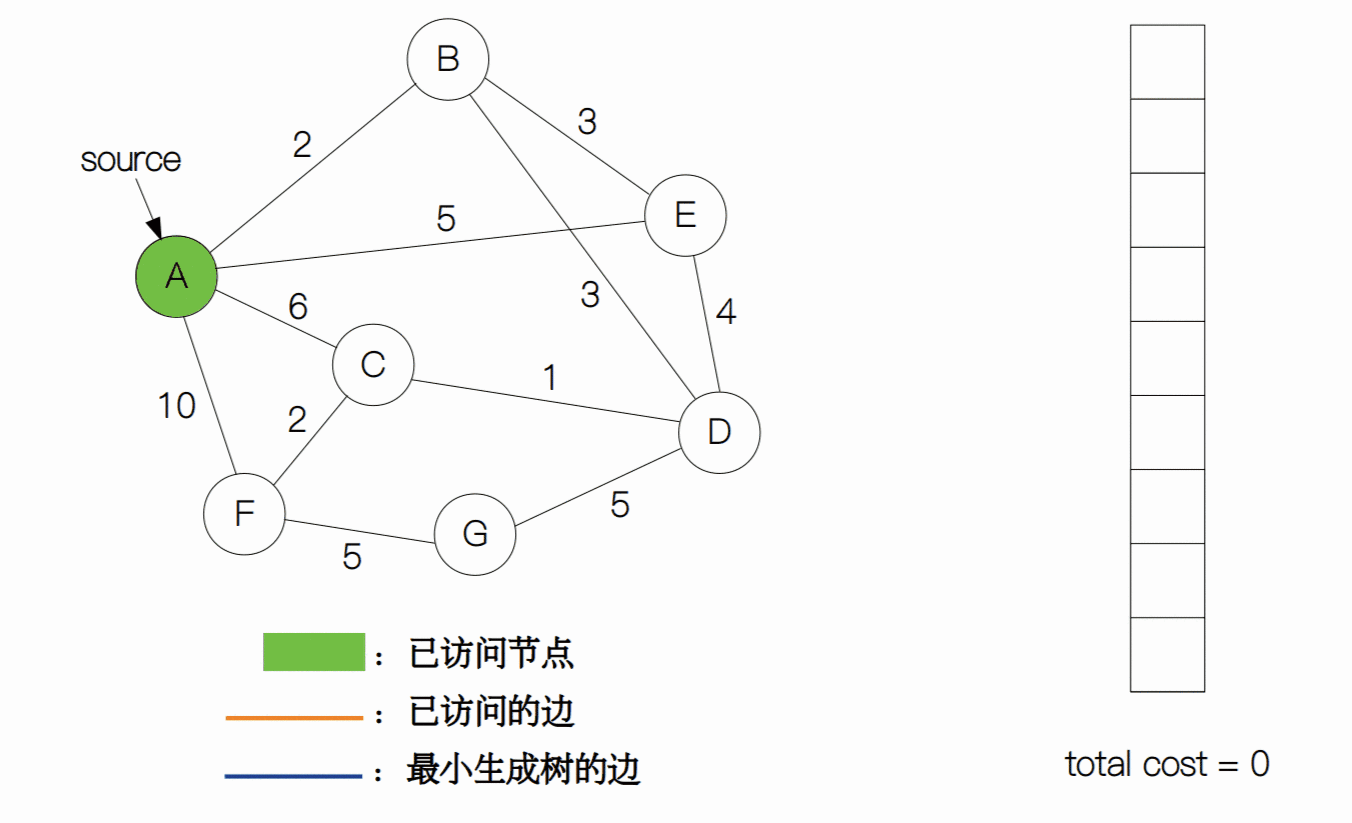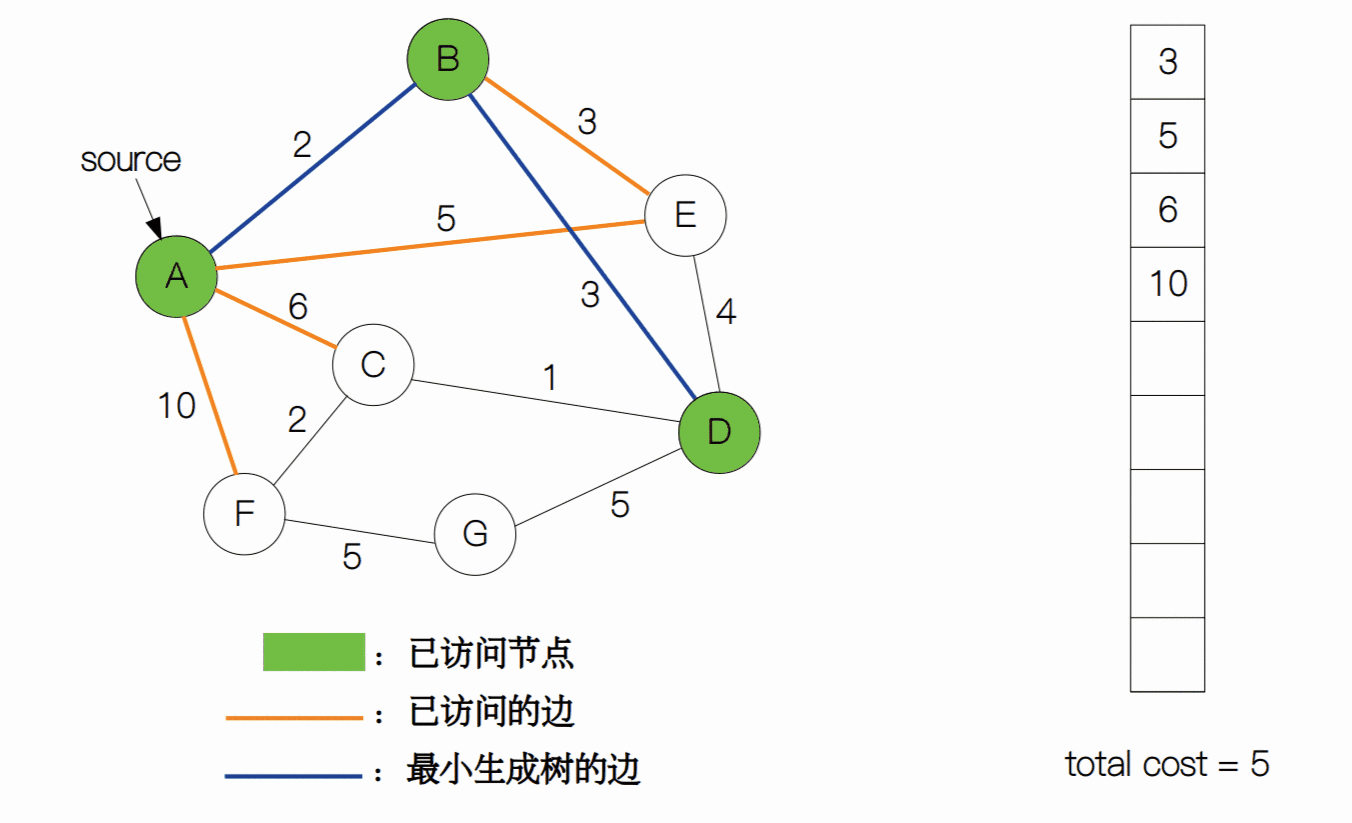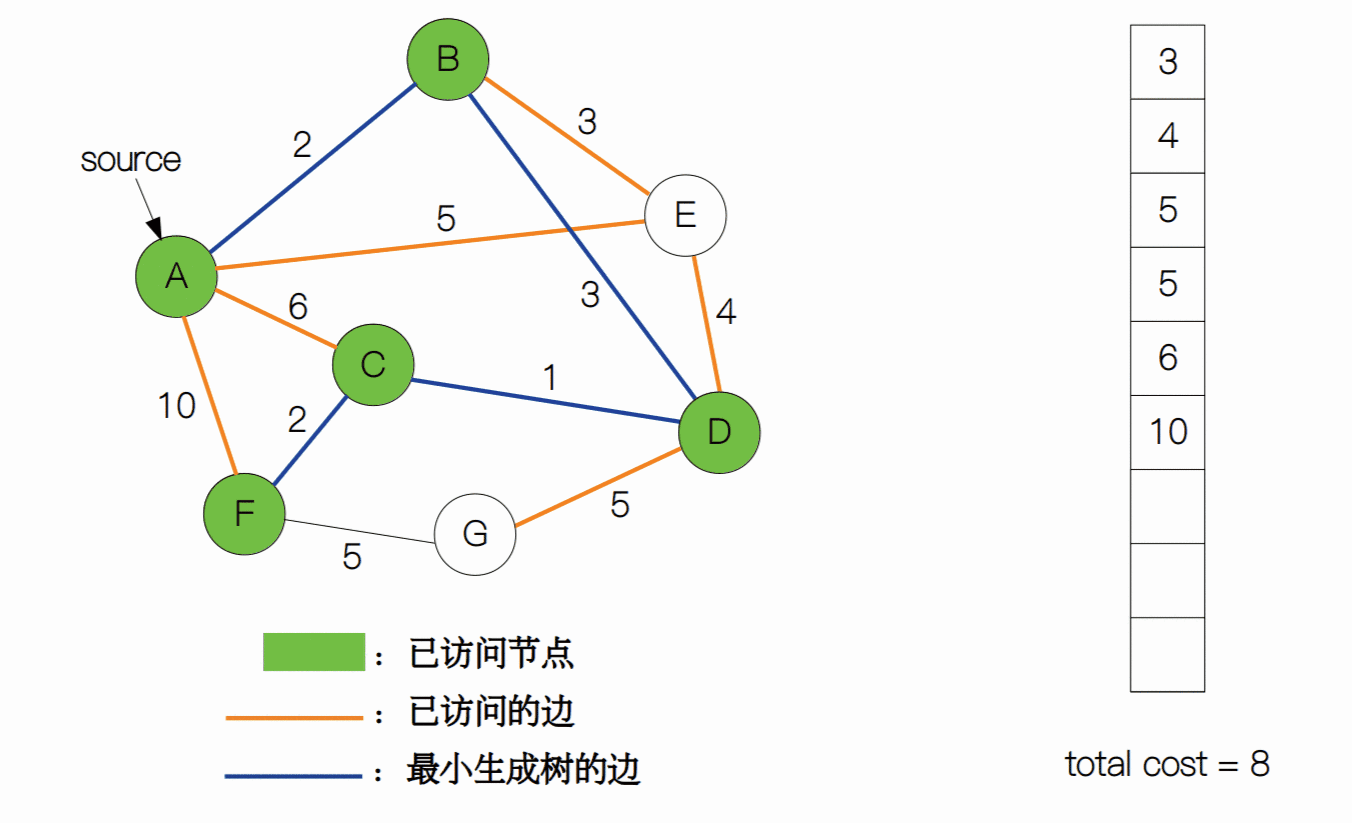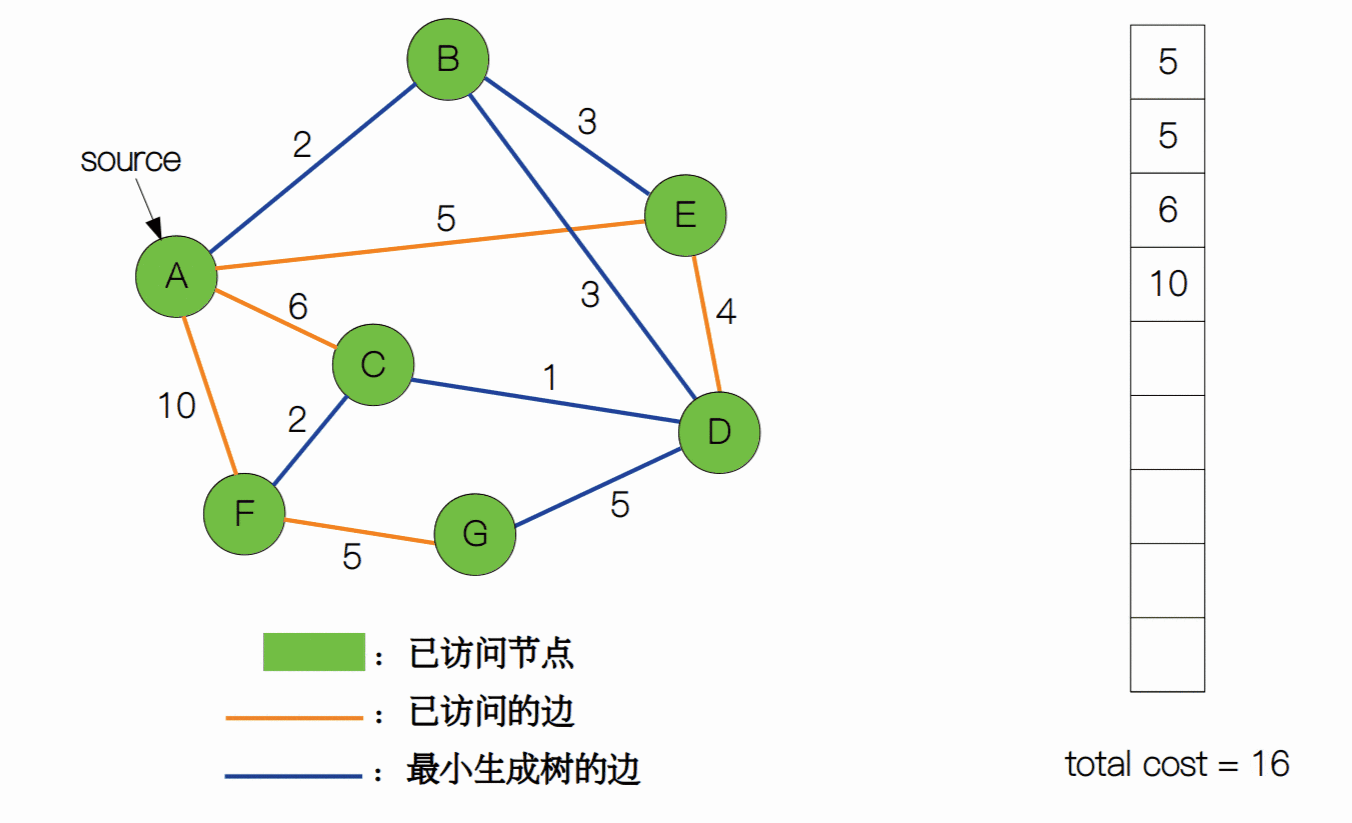
最后，我们来计算一下复杂度。每当一个元素加入到堆中或从堆顶中删除，时间复杂度为都为 Θ(log(|V|))，普林姆算法需要将每一个边加入到堆中，所以建堆的时间复杂度为 Θ(|E|log|V|)。而生成树最少需要 |V| - 1 条边来构成，所以需要执行 |V| - 1 次删除操作（复杂度为 Θ((|V| - 1))log|V|)）。最后总的时间复杂度就为 Θ((|V| - 1 + |E|)log|V|)。

→ 本节全部代码 ←