时空权衡
在前面的章节里,我们知道归并排序是一种高效的排序算法,在任何情况下时间复杂度都为 Θ(nlog n)。但是,它需要用额外的内存空间来暂时储存归并过程中的元素,因此我们可以认为归并排序是以牺牲一部分内存空间为代价来获得时间的高效性。相反,如果内存空间有限,我们就必须以牺牲时间为代价来保证空间不被过度使用。像上面所说的那样,在设计一个算法的过程中同时考虑时间复杂度和空间复杂度,并且在这两者中找到一个平衡点的过程我们把它称作时空权衡(time and space trade-off)。

在通常情况下,我们都认为时间更宝贵,而空间相对廉价。因此在大多数情况下,我们都是以牺牲空间的方式来减少运行时间。
计数排序
计数排序(counting sort)就是一种牺牲内存空间来换取低时间复杂度的排序算法,同时它也是一种不基于比较的算法。这里的不基于比较指的是数组元素之间不存在比较大小的排序算法,我们知道,用分治法来解决排序问题最快也只能使算法的时间复杂度接近 Θ(nlog n),即基于比较的时间复杂度存在下界 Ω(nlog n),而不基于比较的排序算法可以突破这一下界。
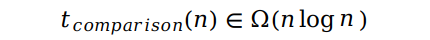
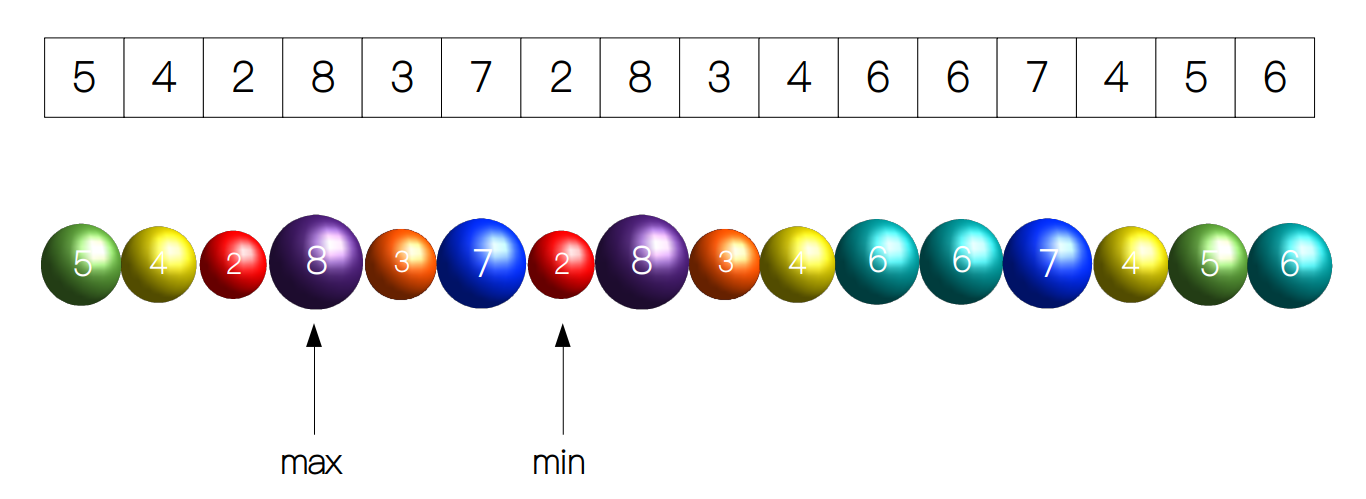
下面我们就来介绍一种不基于比较的排序算法:计数排序。我们用一种通俗方式来理解这个过程过程。如下图所示,假设我们用不同大小的小球来表示每一个数组元素的值,我们的目标是使小球从小到大以次排列。

首先我们需要知道最大的球和最小的球分别对应的元素,这里最大的对应 8,最小的对应 2。
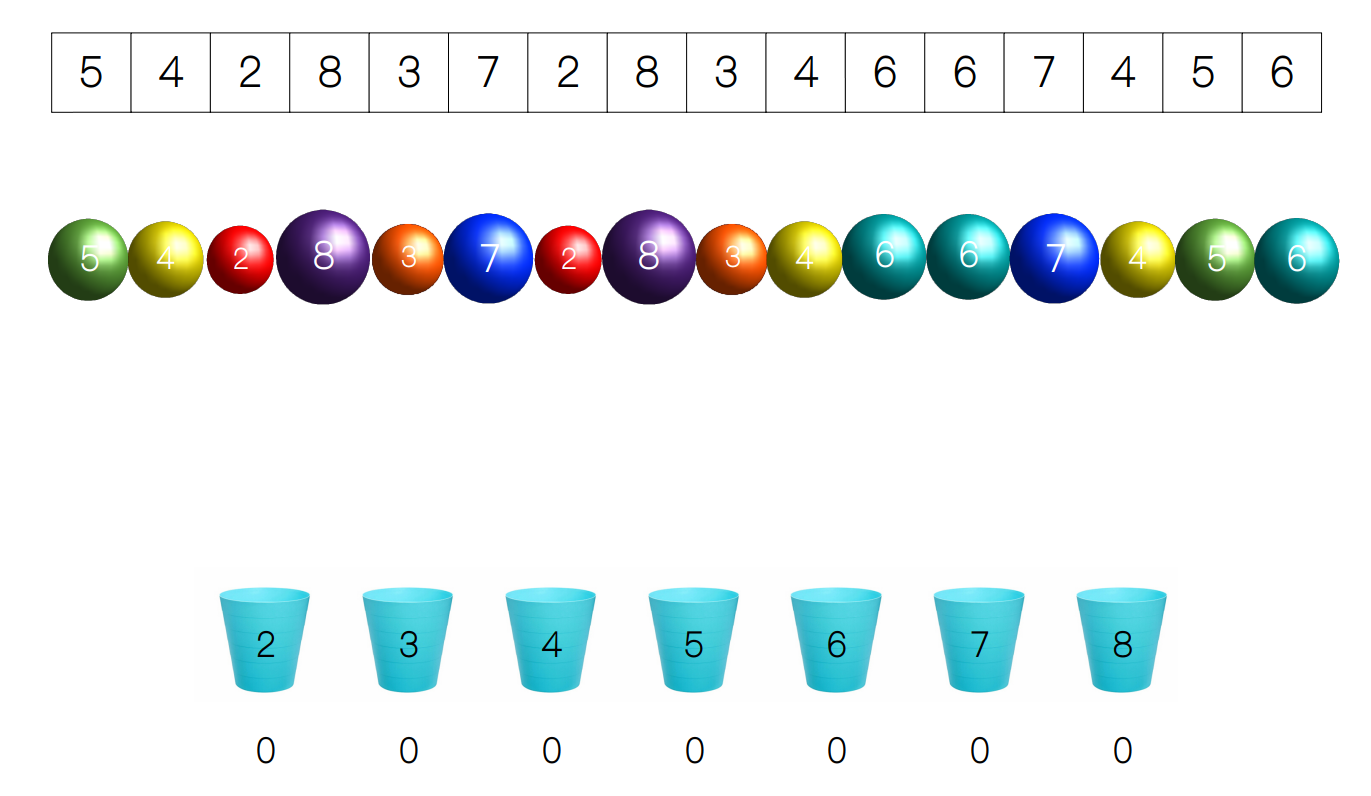
然后我们需要用 8 - 2 + 1 = 7 个计数器来分别统计 2 到 8 之间每种小球的个数(假设 2 到 8 之间的小球对应的元素均为整数),下图中我们用带有标记的桶来表示。
接下来,我们遍历所有的小球,将每个值为 i 的小球放入到第 (i - 2 + 1) 个桶中,比方说第一个小球的值为 5,那么我们就把它放到标号为 5,也就是从左往右第 4 个桶中,放入后计数器加 1。

最后,我们从左往右依次将每个桶里的小球取出,每取出一个小球,对应桶的计数器减 1,直到计数器为 0,将所有桶内的小球都取出后,小球就是从小到大排列了。

我们用一个动画(来源于网络)来完整地看一看这个过程。
def counting_sort(array):
largest = max(array); smallest = min(array) # 获取最大,最小值
counter = [0 for i in range(largest-smallest+1)] # 用于统计个数的空数组
idx = 0
for i in range(len(array)):
counter[array[i]-smallest] += 1
for j in range(len(counter)):
while counter[j] > 0:
array[idx] = j + smallest
idx += 1
counter[j] -= 1
return array
整个过程需要遍历两次数组,一次是遍历长度为 n 的数组,另一次是从计数器(假设有 k 个计数器)中遍历,因此时间复杂度为 Θ(n+k)。而在计数排序的过程中用到了长度为 k 的额外数组,故空间复杂度为 Θ(k)。
我们可以看到计数排序突破了基于比较的排序算法效率的下界,达到了线性的复杂度,是到目前为止我们接触到的最快的算法。我们还是可以通过运行时间来间接反应这一结论,大家可以将下面的结果和前面复杂度为 Θ(nlog n) 的排序算法进行对比。
>>> python "counting sort.py"
>>> 平均比较次数:0
平均运行时间:0.0172 s
→ 本节全部代码 ←