介绍
无论是 AVL 树还是红黑树,它们都有个共同的特点:每个节点最多只能存放一个值,并且最多只有两个子节点。我们知道,AVL 树和红黑树的查找效率接近于 Θ(log n),这得益于我们将树的结构做了调整,使得树的高度尽可能的减小,来达到平均搜索的次数减少。因此,从这一点可以启发我们,要想使查找效率高,我们就要尽可能的减小树的高度,于是就有了多路查找的树,就好比树根有多条分叉一样,这里我们只说最经典的 2-3 树。

两种节点
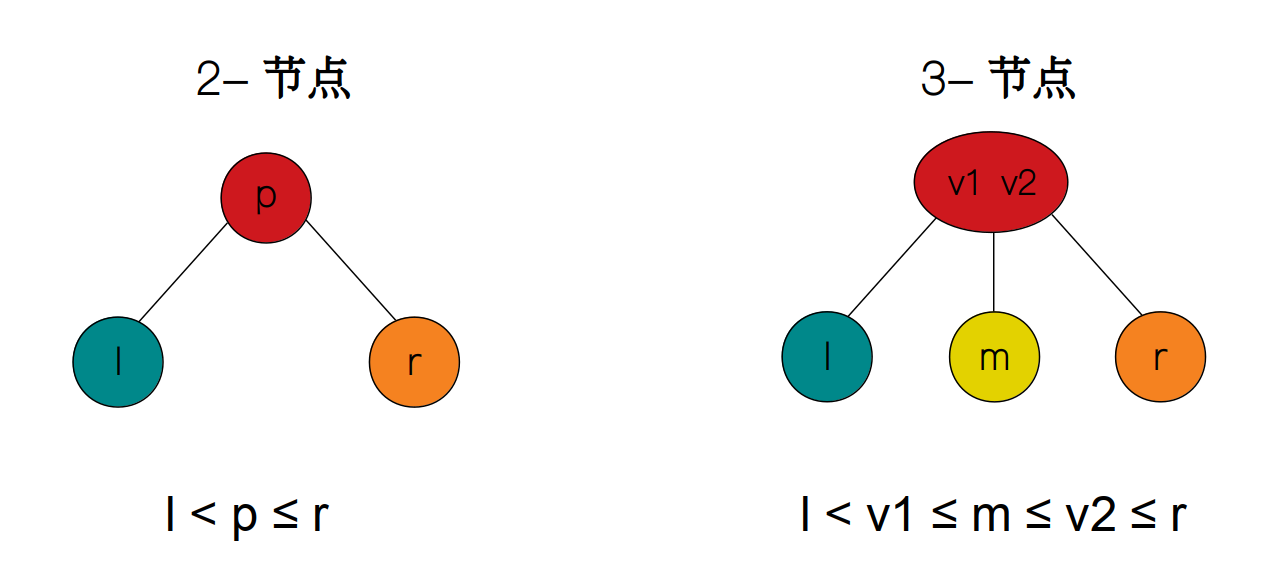
2-3 树从字面上很难理解它要传达出的意思,因此我们要首先明白一个概念,所有二叉树的节点最多只有 2 个子节点,我们把这种节点称作 2-节点,它跟二叉树的节点一样,左孩子的值小于根节点的值,右孩子的值大于等于根节点的值,同理,3-节点就是指最多只有 3 个子节点的节点,而每个节点最多可以存放两个值。假设根节点的两个值分别为 v1, v2,左中右 3 个孩子节点的值分别为 l, m, r,那么它们之间的关系就为 l < v1 ≤ m ≤ v2 ≤ r 。所以,2-3 树就是指由 2-节点和(或) 3-节点共同构成的树。
这里为了方便用代码来实现 2-3 树,我们将所有的节点都看做 3-节点,在表示 2-节点时候只需稍微做一下调整就好。另外,为了更方便后面的插入和删除操作,我们定义了判断节点是否为叶子节点的方法is_leaf,判断节点是否是 3-节点的方法is_full,以及获取孩子节点和兄弟节点的方法get_child和brother。
class Node(object):
def __init__(self, value):
self.value1 = value
self.value2 = None
self.left = None
self.mid = None
self.right = None
self.parent = None # 父节点
def is_leaf(self):
# 判断节点是否为叶子节点
return not self.left and not self.mid and not self.right
def is_full(self):
# 判断节点是否为 3-节点
return self.value2 is not None
def get_child(self, value):
# 给定一个值,返回要搜索的下一个子节点
if self.value2: # 3-节点
if value < self.value1:
return self.left # 返回左节点
elif value < self.value2:
return self.mid # 返回中间节点
return self.right # 返回右节点
else: # 2-节点
if value < self.value1:
return self.left
return self.right
# 返回有 3-节点的兄弟节点
def brother(self):
# 只有父节点存在时才返回兄弟节点
if self.parent:
# 父节点为 2-节点时
if not self.parent.is_full():
if self.parent.left is self:
return self.parent.right
return self.parent.left
# 父节点为 3-节点时
else:
if self.parent.mid is self:
if self.parent.right.is_full():
return self.parent.right
if self.parent.left.is_full():
return self.parent.left
# 左右节点任选一个
return self.parent.right
return self.parent.mid
搜索
和二叉搜索树一样,2-3 树也是从根节点出发,只是每次可能需要跟两个值进行比较,如果和值value相等,我们就返回该节点;否则就调用前面Node类的get_child方法,获取子节点,然后再在子节点中继续搜索,如查找失败则返回None。
class TwoThreeTree(object):
def __init__(self):
self.root = None
def search(self, value):
# 树的根节点为空就抛出异常
if not self.root:
raise ValueError("The tree is null")
return self.search_node(self.root, value)
def search_node(self, root, value):
if not root:
return None # 查找失败
if value == root.value1 or value == root.value2:
return root # 查找成功
return self.search_node(root.get_child(value), value) # 从对应的孩子节点中继续查找
插入
特点
2-3 树的插入操作跟二叉树既有相似的地方又有不同的地方。相似之处在于两者都要先通过搜索,找到插入的位点;不同之处在于这个插入的位点总是位于叶子节点,而非一个任意节点,另外,2-3 树的插入操作是将插入值value直接放进待插入的节点,而不是新建一个节点。
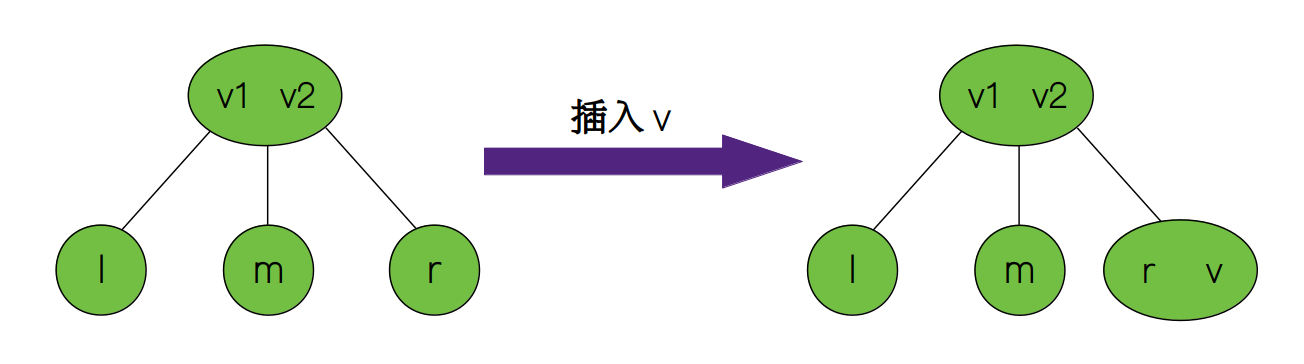
但是,2-3 树存在两种类型的节点(2-节点和 3-节点),因此我们要分为两种情况讨论:
插入到 2-节点
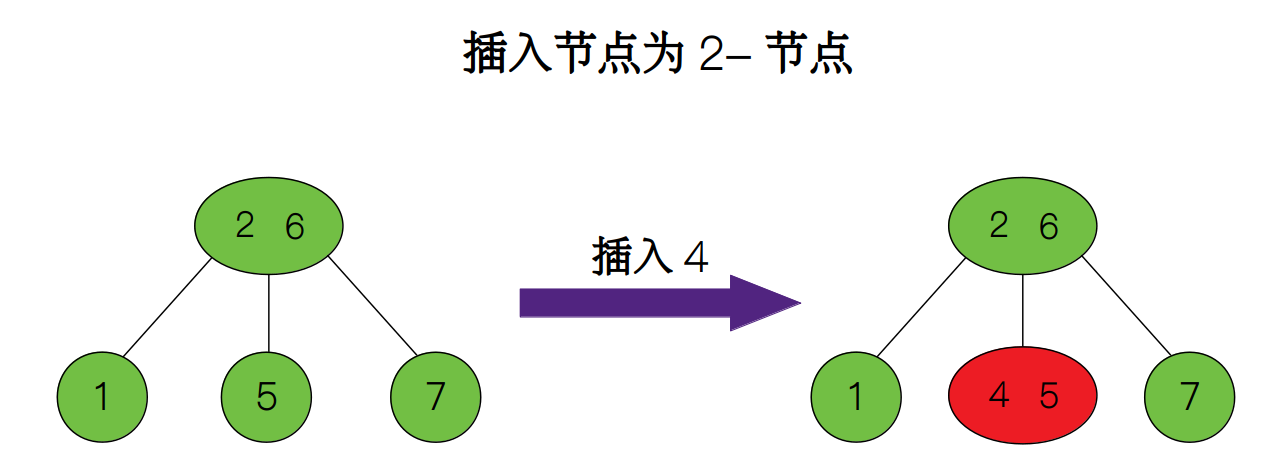
将一个值value插入到 2-节点的情况很简单,只需要将value放入正确的位置使之变为 3-节点即可。因此,我们用一个函数put_item来实现它。
def put_item(self, leaf, value):
if value < leaf.value1:
leaf.value2 = leaf.value1
leaf.value1 = value
else:
leaf.value2 = value
例如我们把 4 插入到下面的树中,将会得到:
插入到 3-节点
插入到 3-节点的情况会比较麻烦,因为节点已经满了,在这种情况下,2-3 树采用的策略是分裂成两个节点,下面就来介绍一下节点是如何分裂的。
分裂
分裂的过程可以概括为,原节点保留三个值(新来的值以及节点中原有的两个值)中的最小值,新分裂出的节点用来存放最大值,而将中间值向上传递到父节点中,换句话说就是将中间值插入到父节点中,因为父节点是 2-节点还是 3-节点未知,所以我们要分情况讨论:
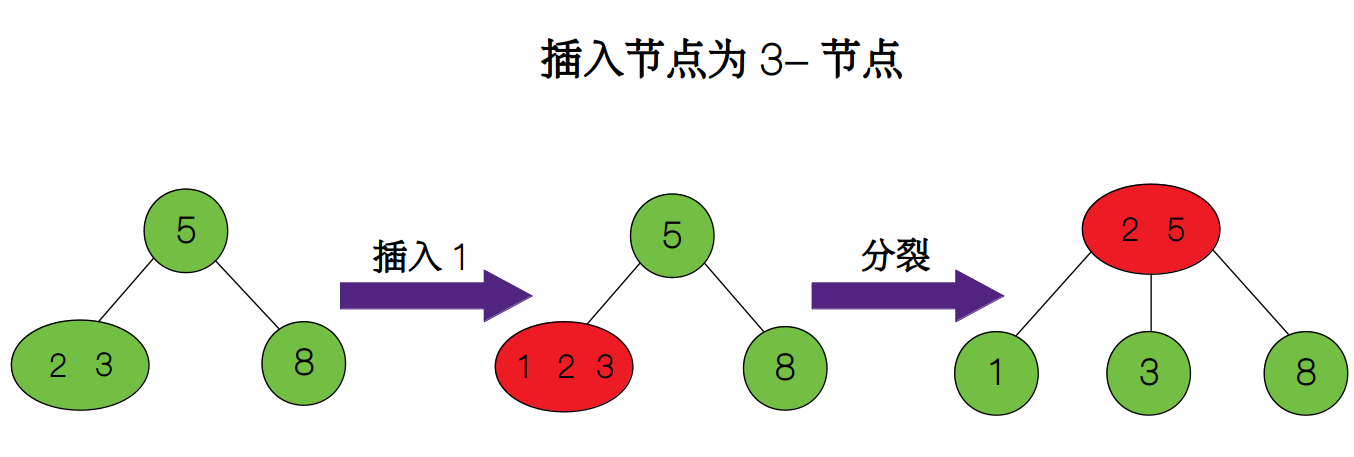
- 情况 1:父节点存在,且为 2-节点。这种情况下只需将中间值插入到父节点即可。下面中的例子中,如果要在向 2-3 树中插入 1,插入后原节点分裂成两个节点,并将 2 传递到父节点,最后父节点变为 3-节点。
- 情况 2:父节点存在,且为 3-节点。这时父节点也需要分裂,因此分裂后父节点再将其中间值向上传递,整个过程递归地进行直到遇到根节点。例如,我们还是在绿色的 3-节点中插入 9,插入后原节点分裂成两个节点,并将 8 传递到父节点中,这时发现父节点也为 3-节点,所以父节点的父节点也要分裂,分裂后我们把中间值 6 传递到上一层。

- 情况 3:父节点不存在,也就是当情况 2 中递归到根节点时,我们要新建一个节点,用来保存由下一层分裂出的中间值,并使分裂出的两个节点成为新节点的左右孩子,最后让新节点成为树的根节点,此时树的高度加 1。紧接着上面的例子来看,此时中间值 6 传递的上一层为空。因而,我们需要用一个新节点来存放 6,并将其左右孩子指针指向分裂的两个节点。

这个过程我们用两个函数来实现,其中split表示一次分裂的过程,返回中间值以及新分裂出的节点。另一个函数put_item_full用来实现上述的 3 种情况。
def split(self, leaf, value):
new_node = Node(None)
# `value1` 为中间值
if value < leaf.value1:
pvalue = leaf.value1
leaf.value1 = value
new_node.value1 = leaf.value2
# `value` 为中间值
elif value < leaf.value2:
pvalue = value
new_node.value1 = leaf.value2
# `value2` 为中间值
else:
pvalue = leaf.value2
new_node.value1 = value
leaf.value2 = None
return pvalue, new_node
def put_item_full(self, leaf, value):
pvalue, new_node = self.split(leaf, value) # 获得由叶子节点得到的中间值和新分裂的节点
# 从叶子节点出发,向上递归到根节点
while leaf.parent:
# 父节点为 2-节点,直接插入,然后退出循环
if not leaf.parent.is_full():
self.put_item(leaf.parent, pvalue)
# 叶子节点为父节点的左孩子
if leaf.parent.left is leaf:
leaf.parent.mid = new_node
# 叶子节点为父节点的右孩子
else:
leaf.parent.mid = leaf; leaf.parent.right = new_node
new_node.parent = leaf.parent
break
# 分裂父节点并根据不同的情况来调整指针
else:
pvalue_p, new_node_p = self.split(leaf.parent, pvalue)
# 情况 1:分裂的节点是父节点的左孩子
if leaf.parent.left is leaf:
new_node_p.left = leaf.parent.mid; leaf.parent.mid.parent = new_node_p
new_node_p.right = leaf.parent.right; leaf.parent.right.parent = new_node_p
leaf.parent.right = new_node; new_node.parent = leaf.parent
# 情况 2:分裂的节点是父节点的中间孩子
elif leaf.parent.mid is leaf:
new_node_p.left = new_node; new_node.parent = new_node_p
new_node_p.right = leaf.parent.right; leaf.parent.right.parent = new_node_p
leaf.parent.right = leaf.parent.mid
# 情况 3:分裂的节点是父节点的右孩子
else:
leaf.parent.right = leaf.parent.mid; temp = leaf.parent.right
new_node_p.left = leaf; leaf.parent = new_node_p
new_node_p.right = new_node; new_node.parent = new_node_p
leaf = temp
leaf.parent.mid = None # 变为 2-节点
leaf = leaf.parent; pvalue = pvalue_p; new_node = new_node_p # 对应节点向上移动
# 如果递归到根节点,则创建一个新的根节点
else:
new_root = Node(pvalue)
new_root.left = leaf; new_root.right = new_node
leaf.parent = new_root; new_node.parent = new_root
最后,我们写出插入操作的两个主函数,用来分别控制不同情况下采用的不同插入策略。
def insert(self, value):
if not self.root:
self.root = Node(value)
return
self.insert_node(self.root, value)
def insert_node(self, root, value):
# 搜索`value`,直到遇到叶子节点
while not root.is_leaf():
root = root.get_child(value)
# 节点为 2-节点
if not root.is_full():
self.put_item(root, value)
# 节点为 3-节点
else:
self.put_item_full(root, value)
删除
删除操作会更加麻烦,网上的 2-3 树教程通常到插入操作就结束了,就算有也没有代码的实现,因此,这一部分全都是我自己慢慢写出来的,如果有什么不对或者需要完善的地方,请各位大佬批评指正。
和二叉树一样,首先我们通过调用search找到待删除的节点,然后删除里面的值即可。但是不同的是,2-3 树有两种节点,并且 2-3 树的其中一条性质是所有叶子节点的高度均相等。因此,我们的删除操作要分为主要 5 种情况,下面就来分别看看:
待删除的值在父节点
如果待删除的值在父节点,我们还是和二叉树一样先在父节点中找到前驱,也就是在对应子树中找到最大值,然后交换它们的值,因为 2-3 树的最大值一定出现在叶子节点,所以删除父节点的问题就被转换为了删除叶子节点的问题。
那么前驱怎么找呢?当父节点为 2-节点时,我们从父节点的左子树中找最大值,例如在下面的图中,我们要找 5 的前驱,我们就从 5 的左子树中找最大值,然后交换它们的值。

当父节点为 3-节点,待删除的值为较小者时,我们还是从父节点的左子树找最大值;而如果待删除的值为较大者,我们就从父节点的中间子树中找最大值。例如下图中,3 和 6 的前驱分别为 2 和 5。

寻找前驱节点的代码如下:
def get_predecessor(self, root):
if root.right:
return self.get_predecessor(root.right)
return root
待删除的值在叶子节点
当待删除的值在叶子节点上时,我们又可以分为下面两大类:
叶子节点为 3-节点
这种情况最简单,直接删除即可,3-节点变为 2-节点。

我们定义一个函数remove_item来实现上述过程。
def remove_item(self, node, value):
# 假设节点都为 3-节点
if node.value1 == value:
node.value1 = node.value2
node.value2 = None
叶子节点为 2-节点
当叶子节点为 2-节点时,我们要分别查看兄弟节点和父节点的类型,因此,我们再将它们分为三种情况:
- 情况 1:兄弟节点为 3-节点。这种情况下,我们需要向兄弟节点借一个最近的值,来补充删除后空的叶子节点。下面的例子中,如果删除的值为 6,我们需要向兄弟节点借一个值 8,但借来后发现不满足大小关系(7 ≯ 8),所以我们需要再交换一下父节点和叶子节点的值。

上面的图中只呈现了父节点为 3-节点的情况,事实上,父节点也可以为 2-节点,但处理的方式都一样,这里就不一一画图演示了,在代码中都有详尽的列举。
def leaf_case1(self, node, brother):
node.value1 = None # 叶子节点的值置为空
# 叶子节点为父节点的左孩子
if node is node.parent.left:
node.value1 = node.parent.value1
node.parent.value1 = brother.value1
# 兄弟节点有左孩子
if brother.left:
node.left = node.mid
node.right = brother.left
brother.left.parent = node
brother.left = brother.mid
self.remove_item(brother, brother.value1)
# 叶子节点为父节点的右孩子
elif node is node.parent.right:
if node.parent.is_full():
node.value1 = node.parent.value2
node.parent.value2 = brother.value2
else:
node.value1 = node.parent.value1
node.parent.value1 = brother.value2
# 兄弟节点有右孩子
if brother.right:
node.right = node.mid
node.left = brother.right
brother.right.parent = node
brother.right = brother.mid
self.remove_item(brother, brother.value2)
# 叶子节点为父节点的中间孩子
else:
# 兄弟节点为父节点的右孩子
if brother is node.parent.right:
node.value1 = node.parent.value2
node.parent.value2 = brother.value1
# 兄弟节点有左孩子
if brother.left:
node.left = node.mid
node.right = brother.left
brother.left.parent = node
brother.left = brother.mid
self.remove_item(brother, brother.value1)
# 兄弟节点为父节点的左孩子
else:
node.value1 = node.parent.value1
node.parent.value1 = brother.value2
# 兄弟节点有右孩子
if brother.right:
node.right = node.mid
node.left= brother.right
brother.right.parent = node
brother.right = brother.mid
self.remove_item(brother, brother.value2)
brother.mid = None
node.mid = None
- 情况 2:兄弟节点为 2-节点,父节点为 3-节点。因为兄弟节点为 2-节点,所以就不能向兄弟节点借一个值了,我们转而向父节点借,并与兄弟节点结合,最后父节点从 3-节点变成了 2-节点。

例子中,如果我们要删除 2,删除后我们向父节点借来一个值 5,然后与兄弟节点 6 结合就得到上图的结果。
def leaf_case2(self, node, brother):
node.value1 = None # 叶子节点的值置为空
# 叶子节点为父节点的左孩子
if node is node.parent.left:
self.put_item(brother, node.parent.value1)
# 叶子节点有中间孩子
if node.mid:
brother.mid = brother.left
brother.left = node.mid
node.mid.parent = brother
node.parent.left = brother
self.remove_item(node.parent, node.parent.value1)
# 叶子节点为父节点的右孩子
elif node is node.parent.right:
self.put_item(brother, node.parent.value2)
# 叶子节点有中间孩子
if node.mid:
brother.mid = brother.right
brother.right = node.mid
node.mid.parent = brother
node.parent.right = brother
self.remove_item(node.parent, node.parent.value2)
# 叶子节点为父节点的中间孩子
else:
self.put_item(brother, node.parent.value2)
# 叶子节点有中间孩子
if node.mid:
brother.mid = brother.left
brother.left = node.mid
node.mid.parent = brother
self.remove_item(node.parent, node.parent.value2)
node.parent.mid = None
del node
- 情况 3:父节点和兄弟节点都为 2-节点。这种情况是最麻烦的,首先我们要让父节点和兄弟节点合并。例如下方如要删除 1,则 2 和 3 进行合并。

我们发现原来的父节点内值为空,为了填补这个空节点,我们要再对父节点执行一次删除操作,注意这里我们仅仅只是调整树的结构,而非删除任何值。接下来我们查看这个节点的兄弟节点和父节点,如果它的兄弟节点是 3-节点,我们就向兄弟节点借一个值来填补这个空值,最后调整节点之间的值使之满足大小关系就好了。

如果父节点是 3-节点,那么我们就向其父节点中借一个值来补充这个空值。

假如父节点和兄弟节点都不是 3-节点,我们就再次合并父节点和兄弟节点,并把空节点传递到上一层,然后再看前面的情况是否满足,这就变成了一个递归的过程,当这个空节点是这棵 2-3 树的根节点时,我们就删除这个节点,并且它的孩子节点为树的根节点,此时树的高度减 1。

这样我们就讨论完情况 3 的所有内容了,代码的实现并不难,我们只需要创建一个while循环,然后反复查看兄弟节点和父节点是否为 3-节点,满足就执行对应的函数(leaf_case1或leaf_case2),执行后退出循环,如果while循环正常退出,我们就认为空节点为根节点,因此在else语句中我们将调整self.root为node的子节点,调整后删除node。
def remove_leaf(self, node, value):
# 直接删除,无需调整
if node.is_full():
self.remove_item(node, value)
else:
brother = node.brother()
while node.parent:
# 情况 1
if brother.is_full():
self.leaf_case1(node, brother)
break
else:
# 情况 2
if node.parent.is_full():
self.leaf_case2(node, brother)
break
# 情况 3
else:
node = self.merge(node, brother)
brother = node.brother()
# 循环正常退出
else:
self.root = node.mid
del node
最后我们写出删除操作的主函数remove。
def remove(self, value):
# 树的根节点为空就抛出异常
if not self.root:
raise ValueError("The tree is null")
node = self.search(value) # 搜索待删除元素对应的节点
# 待删除的值在叶子节点
if node.is_leaf():
self.remove_leaf(node, value)
# 待删除的值在父节点
else:
# 从中间子树中寻找前驱
if node.is_full() and node.value2 == value:
predecessor = self.get_predecessor(node.mid)
# 交换值
if predecessor.is_full():
predecessor.value2, node.value2 = node.value2, predecessor.value2
else:
predecessor.value1, node.value2 = node.value2, predecessor.value1
# 从左子树中寻找前驱
else:
predecessor = self.get_predecessor(node.left)
# 交换值
if predecessor.is_full():
predecessor.value2, node.value1 = node.value1, predecessor.value2
else:
predecessor.value1, node.value1 = node.value1, predecessor.value1
self.remove_leaf(predecessor, value)
复杂度分析
来分析一下 2-3 树的复杂度,首先我们要弄明白树的高度 h 和所有键值的个数 n 之间的关系。假设树的全部节点都为 2-节点,那么 n 的数目最少为 1 + 2 + 22 + ··· + 2h = 2h+1 - 1 。如果全部节点都为 3-节点,那么 n = 2·1 + 2·3 + 2·32 + ··· + 2·3h = 3h+1 - 1,因此我们能够得到下面的关系式:
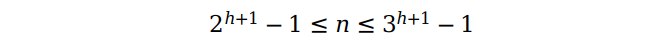
根据上式得到关于 h 的不等式,于是得到:
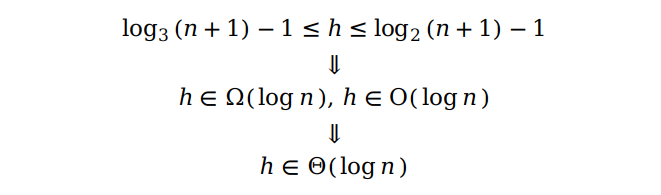
最后得到复杂度为 Θ(log n)。
演示
理解 2-3 树的原理并不难,但用代码实现整个过程会非常的复杂,我花了至少三个晚上的时间才从头到尾地写了出来,所以如果你看不懂代码也没有关系,理解它的原理就好。另外这里有一个非常好的算法可视化网站,它用动画的形式呈现出了各种算法的过程,使我们更好地理解 2-3 树插入和删除过程。
→ 本节全部代码 ←