另一种猜想
上一节我们学习了如何用普林姆算法来解决最小生成树的问题。简单回顾一下,算法一开始从节点集合 V 中任选一个节点作为起始节点,然后选择与之相邻的最小权重的边,如果这条边对应的下一个节点没有被访问过,那么就将这条边作为最小生成树的一部分,否则就看权重第二小的边是否满足要求,以此类推。将上述过程重复执行 |V| - 1 次,我们就可以得到一个图的最小生成树。
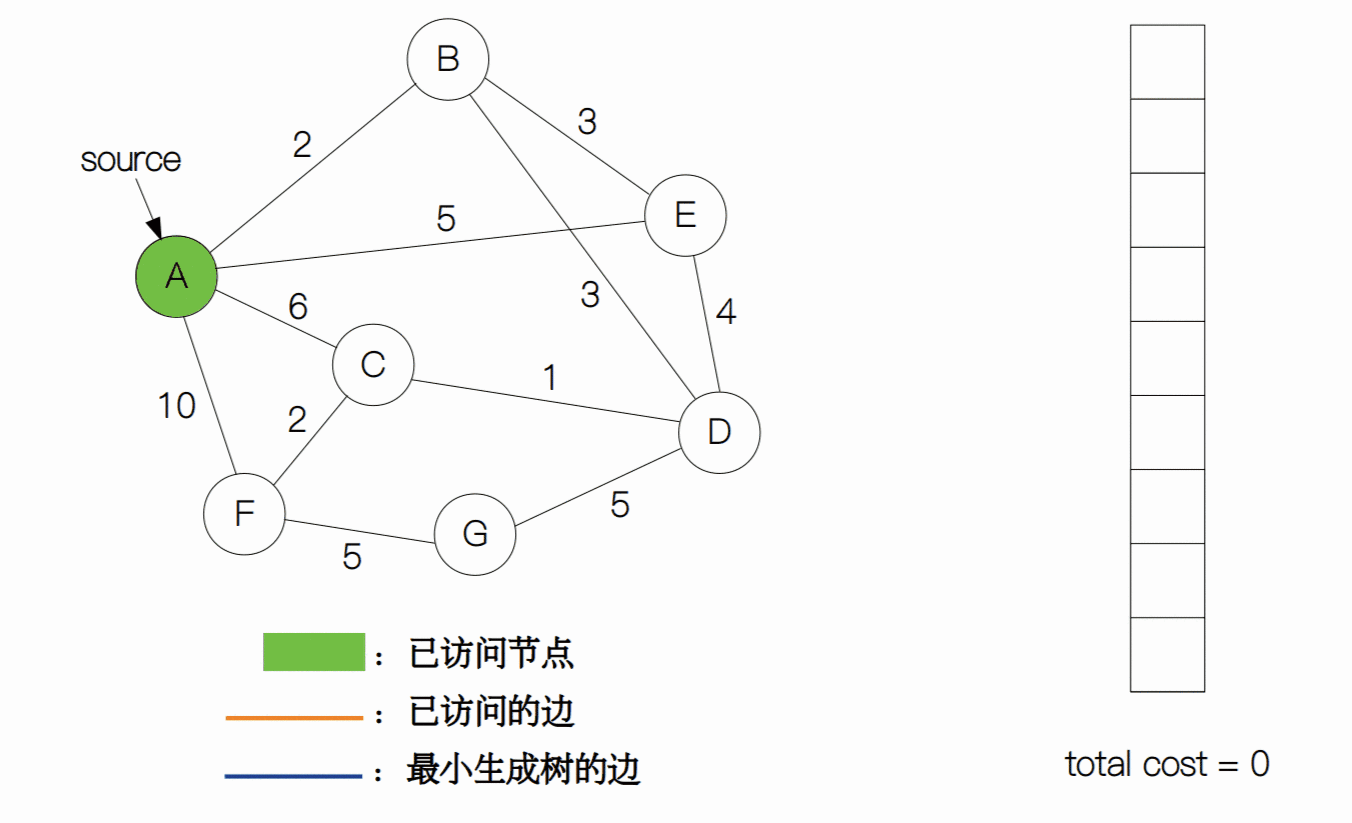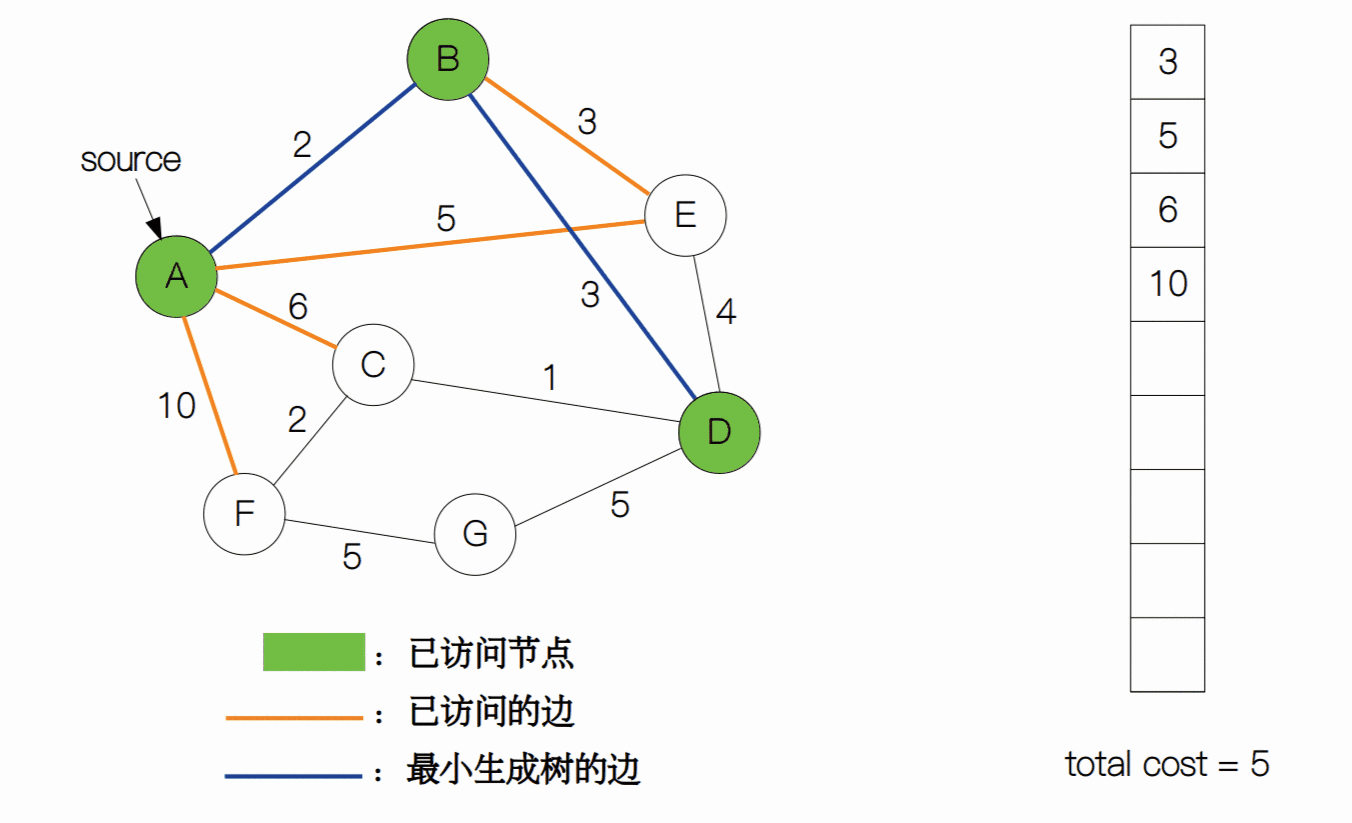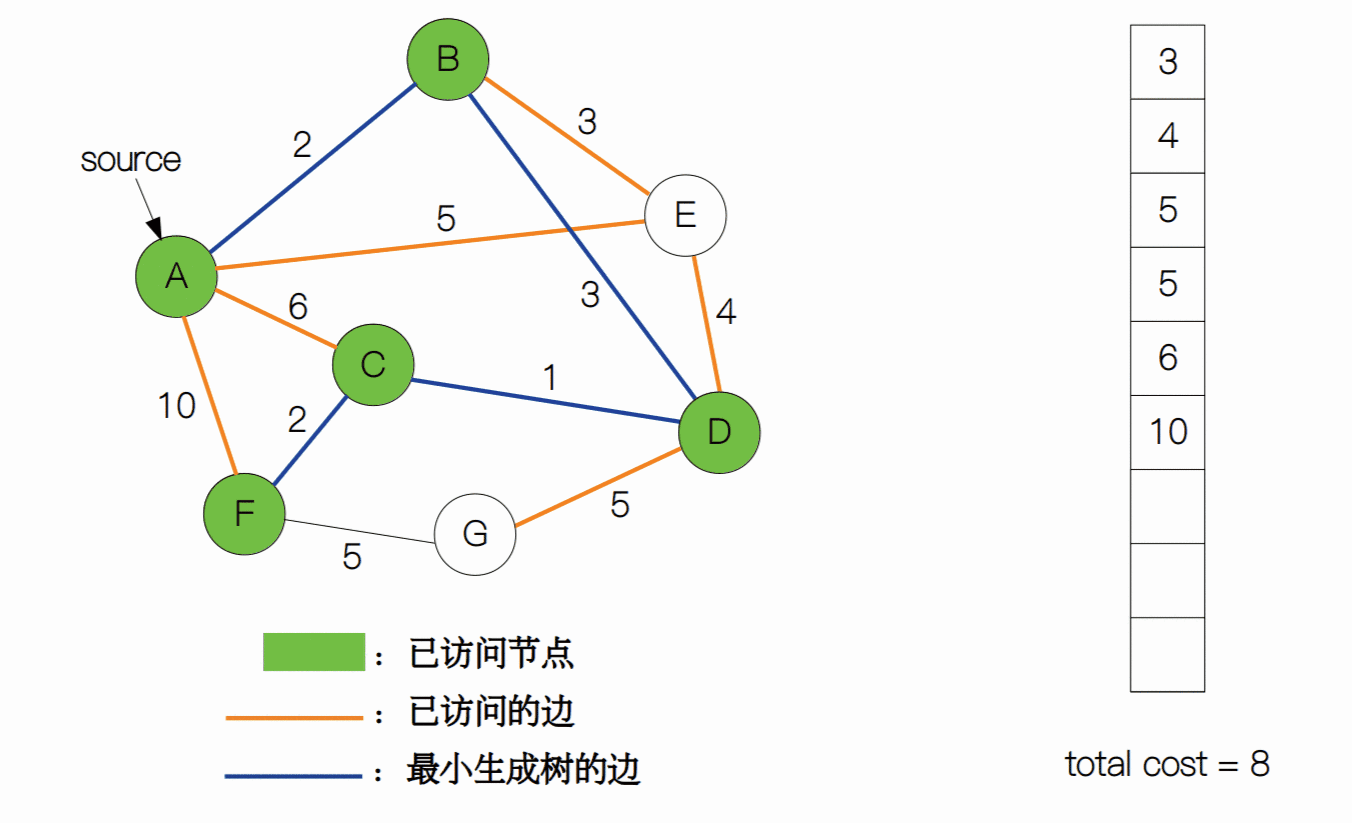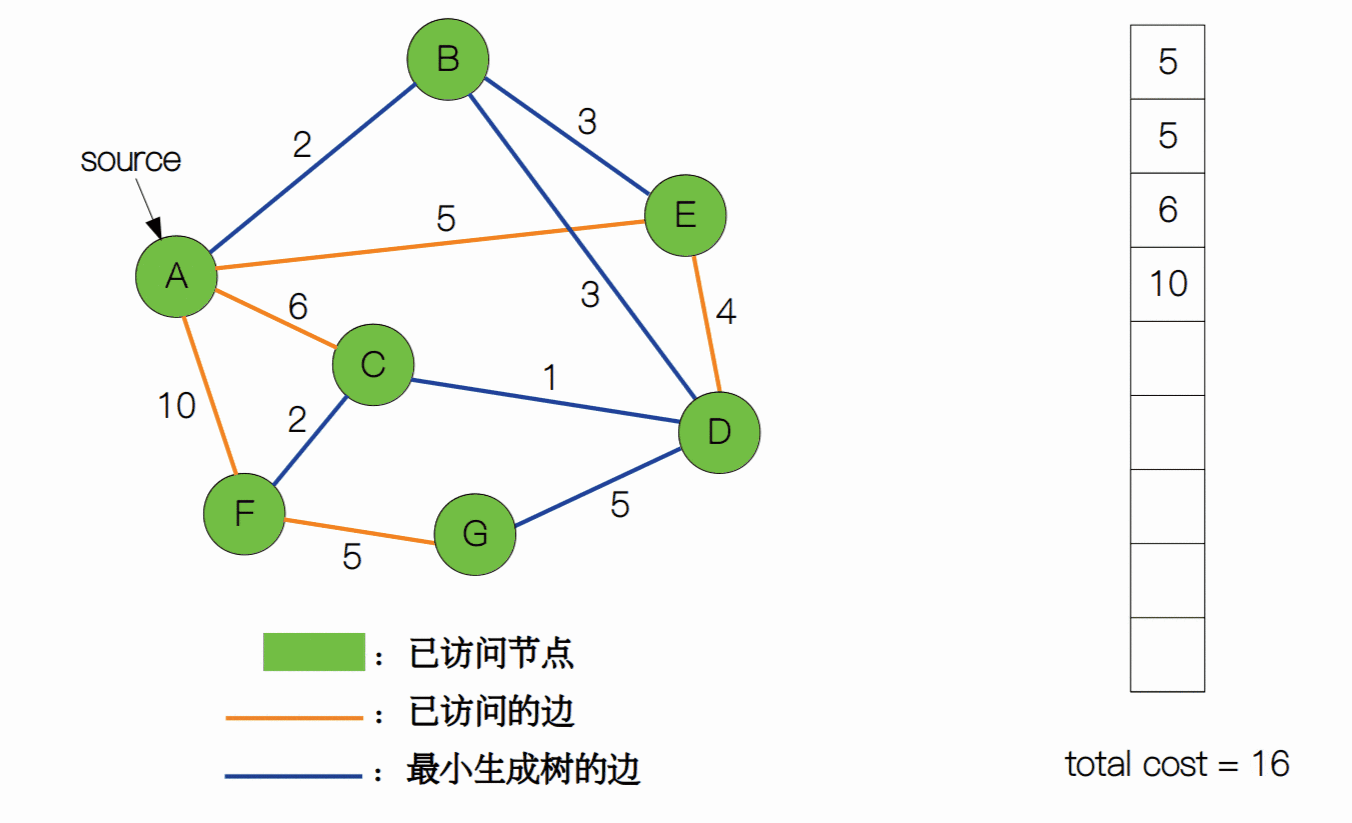
我们看到,普林姆算法是基于现成的图结构来得到最小生成树的。其实,我们还可以这样想:将图中的所有边全部拆开,使节点成为一个个孤立的节点,然后从边集合中取出一部分的边,来使这些节点彼此能够互相连通,并且权值之和最小。
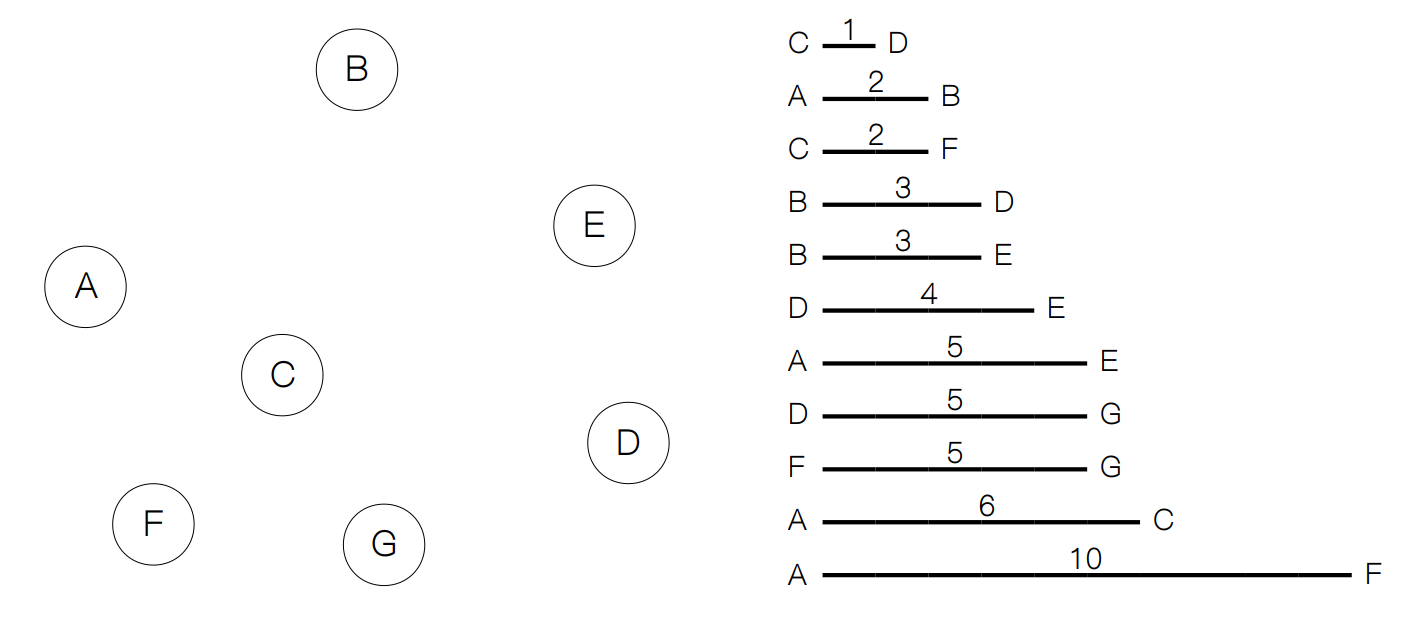
那么,现在的问题是,如何判断两个节点是否连通呢?下面我们就来看看一种特殊的数据结构:并查集(disjoint set)。
并查集
查找是否为同一集合
并查集主要用于判断两个元素是否在同一集合,以及合并两个集合。要想判断两个元素是否在同一个集合,我们只需要让每个元素派出自己所属集合的“代表”(representative),然后判断是否是同一个“代表”即可。这就好比一个刚组建的社团里,同学们相互之间都还不认识,那怎样区分他们是不是同一个班上的人呢?这时只需要每个人都报出自己班上班长的名字,问题就可以得到解决。如果班长是同一个人,那么就是一个班的,否则就不是。例如下面的例子中,两个集合的代表就分别为 A 和 B。
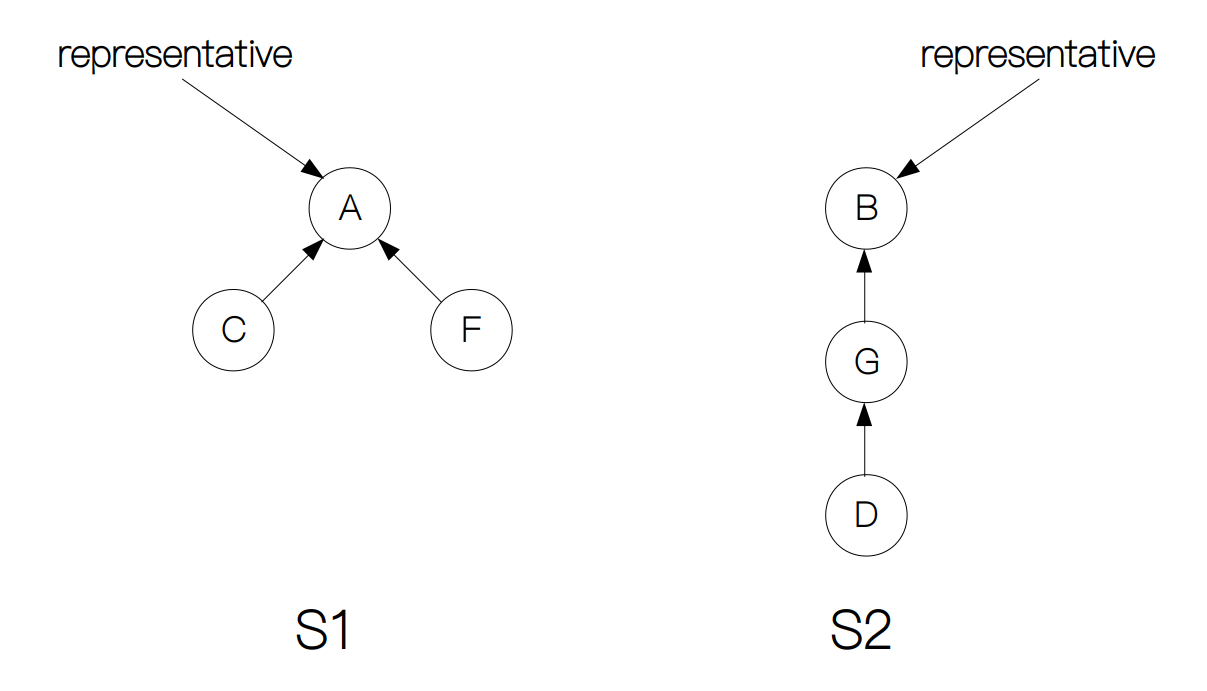
我们首先定义一个Vertex类,使每一个节点在初始化的过程中都指向自身,表示单个节点的“代表”为自身。
class Vertex(object):
def __init__(self, name):
self.name = name
self.parent = self # 指向自身
self.rank = 0
接下来是DisjointSet类的find方法。我们采用递归的方式递归地查找parent为自身的节点,即树的根节点,找到后return。
def find(self, v):
if v.parent is not v:
return self.find(v.parent)
return v
这样我们就可以判断两个节点是否为同一集合啦~
def is_same_set(self, u, v):
return self.find(u) is self.find(v)
合并
合并并查集的方式有很多种,最常用的是基于树的高度的方式(union by rank)。为了使每次查找根节点的次数变少,我们需要将rank小的根节点连接到rank大的根节点上,然后根据公式下面的公式更新合并后根节点的 rank。
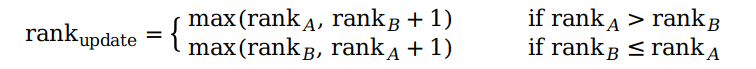
例如下面的两个集合S1和S2,对应根节点 A 和 B 的rank分别为 1 和 2,这时只需要将 A 的父节点指向 B 即可。
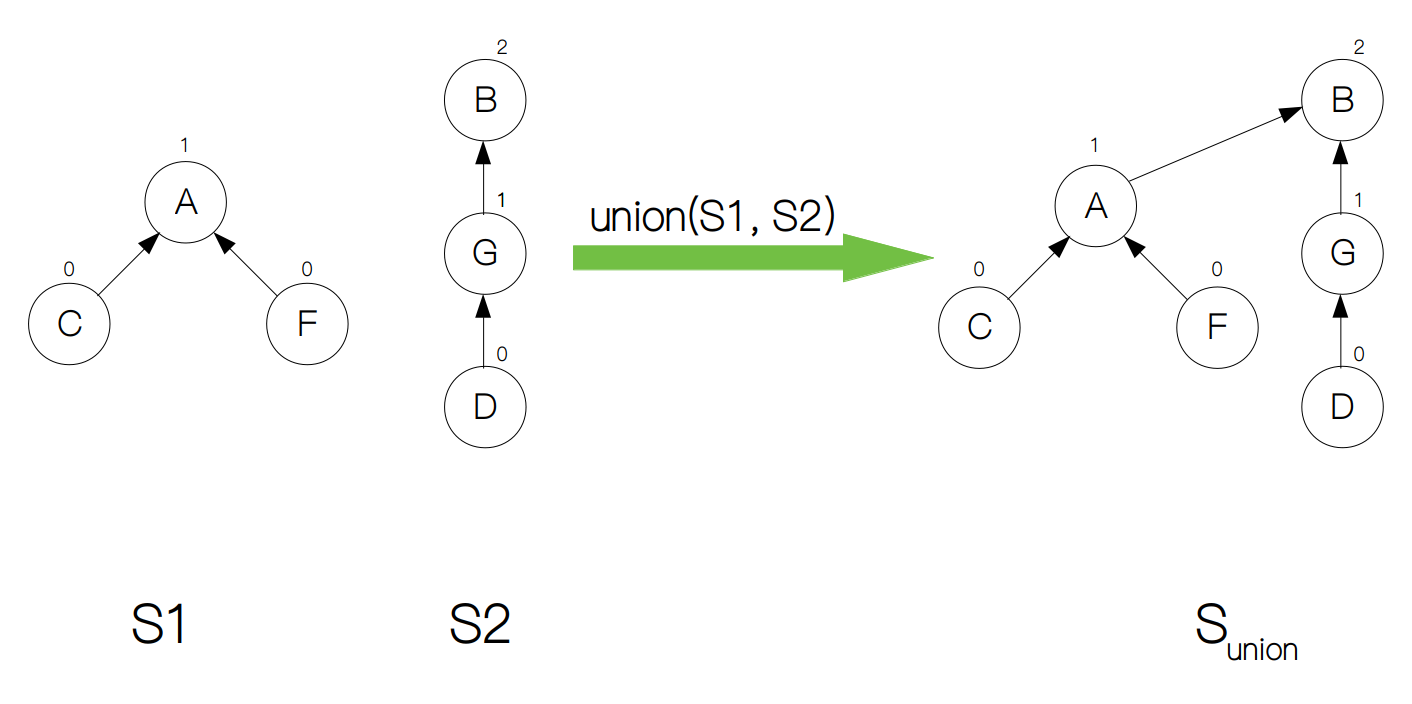
def union(self, u, v):
u_rep = self.find(u); v_rep = self.find(v) # 获取根节点
# u_rep 的高度大于 v_rep 的高度
if u_rep.rank > v_rep.rank:
v_rep.parent = u_rep
u_rep.rank = max(u_rep.rank, v_rep.rank+1)
# u_rep 的高度小于等于 v_rep 的高度
else:
u_rep.parent = v_rep
v_rep.rank = max(v_rep.rank, u_rep.rank+1)
克鲁斯卡尔算法
知道了如何判断两个元素是否在一个集合中,以及怎样将其合并,我们就可以实现克鲁斯卡尔算法了,算法流程如下:
- 第一步:新建一个图
G',它保留了G中的节点,但没有边,每个节点是一个独立的集合。 - 第二步:将图中所有的边
E按照权值从小到大依次排列。 - 第三步:从排好序的
E中依次取出最小权值的边e,判断e连接的节点u和v是否属于同一个集合,如果是就添加到图G中。 - 第四步:重复第三步,直到最终
G’中的边的数目为 |V| - 1 。
为了更好地理解这个过程,我做了一个 gif 动图。其中,我将不满足条件的边打上了 “×”,而用蓝色的线段表示生成树。
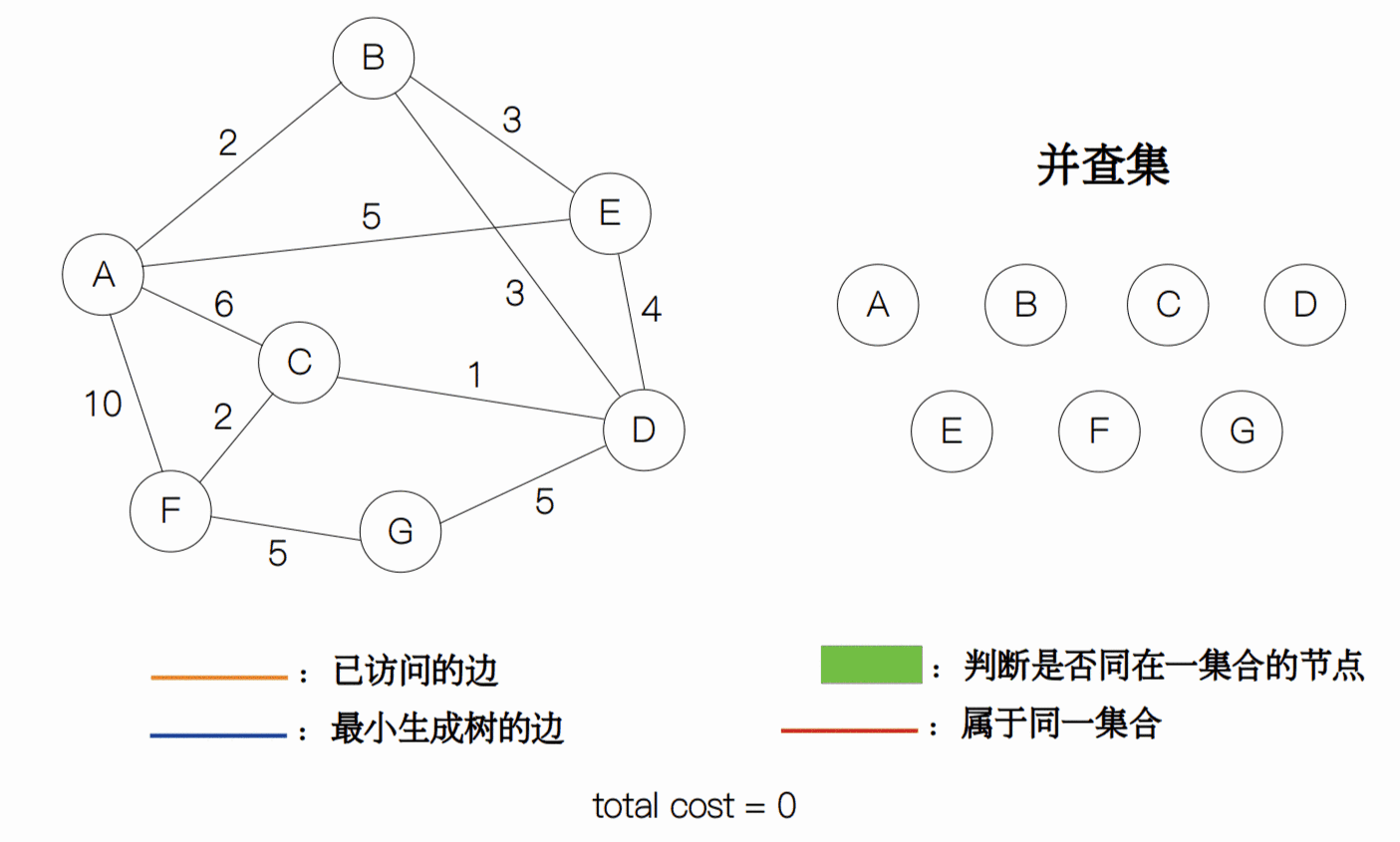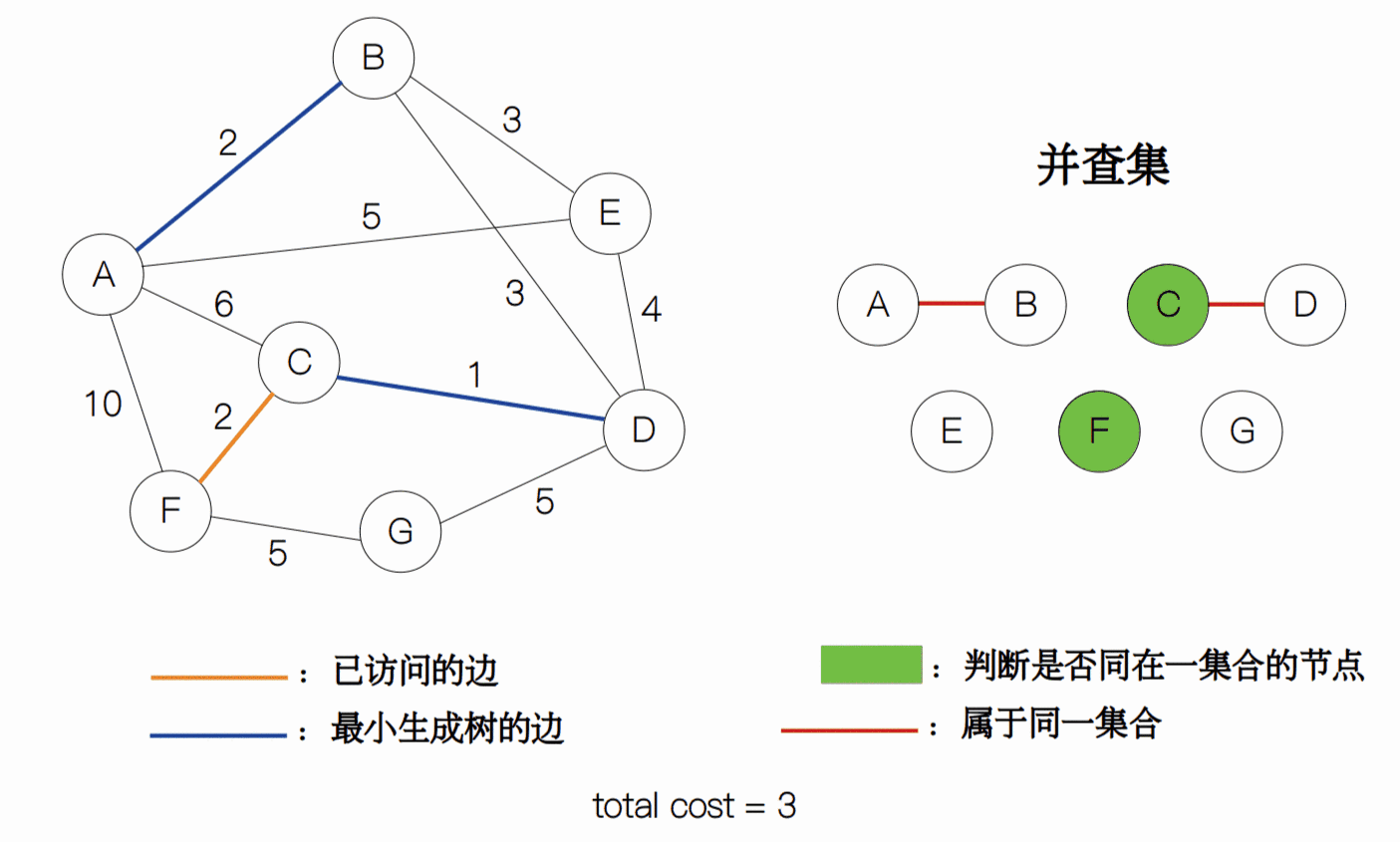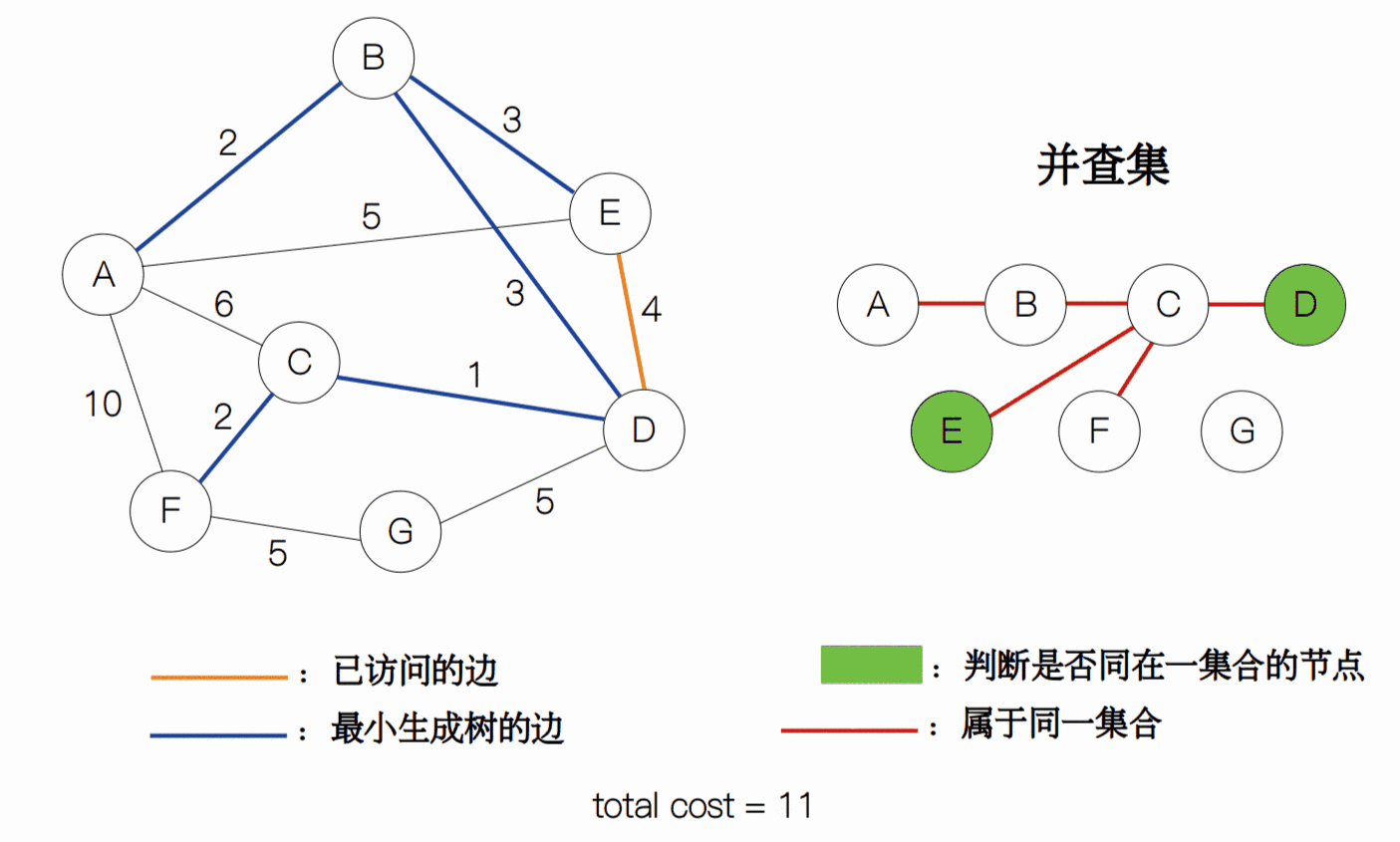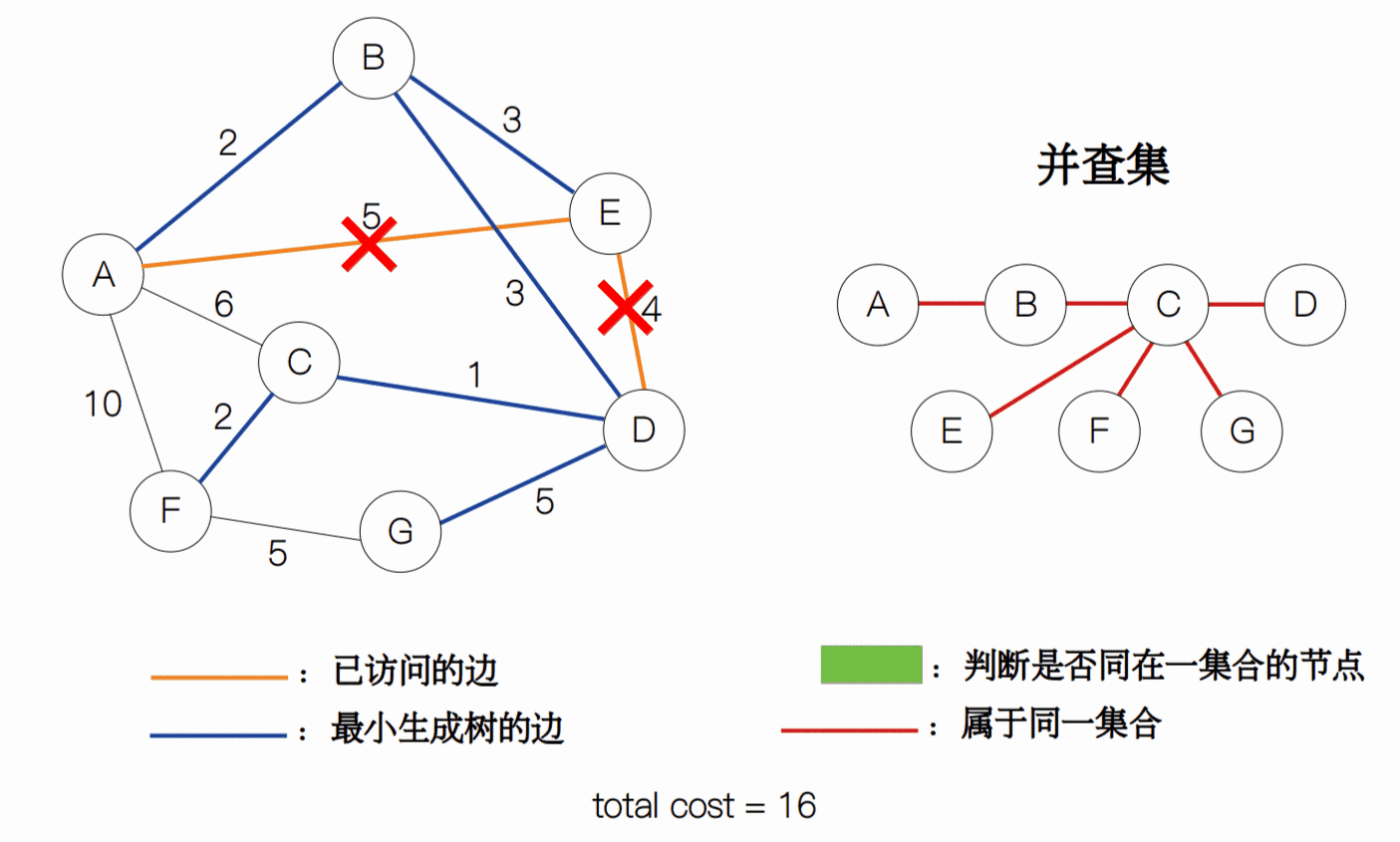
整个过程的代码如下:
def Kruskal(G):
V, E = G # 从 G 中获取节点集合和边集合
E.sort(key=lambda x: x.weight) # 所有的边按权值从小到大排序
total_cost = 0
encounter = 0 # 已处理节点
d_set = DisjointSet()
for e in E:
u = e.pre; v = e.next # 从边中获取相邻节点
# 判断两个节点是否在同一集合内
if not d_set.is_same_set(u, v):
print(u.name + '--' + v.name)
d_set.union(u, v)
encounter += 1
total_cost += e.weight
else:
continue
# 生成树建好就退出循环
if encounter >= len(V) - 1:
break
return total_cost
最后来看看克鲁斯卡尔的时间复杂度。它主要分为三个部分,首先我们要对 |V| 个节点进行初始化,所以第一部分的复杂度为 Θ(|V|);然后,我们要对所有边E进行排序,用基于比较的排序算法,我们最快能够达到 Θ(|E|log|E|) 的复杂度;最后,我们判断两个节点是否属于一个集合,由于树的高度和节点数 |V| 呈现一个近似对数关系,而我们要对 |E| 条边进行判断,因此这一部分的时间复杂度就为 Θ(|E|log|V|)。由于在比较稠密的图中,边的个数大于节点的个数,所以总的复杂度我们取较大的 Θ(|E|log|E|)。
→ 本节全部代码 ←