背景
当我们在家中享受着互联网给我们带来的便利时,你是否想过你的电脑或手机是怎样把这些请求发送到服务器端,而服务器端又怎样把数据包发送到我们的设备的呢?要知道,互联网是由数以亿计的计算机相互连接而成,我们在发送一个数据包时,网络中的路由器会充当接收并转发的中转站,并且这些路由器总是将数据发给离它最近的路由器,在网络中这里的最近指的是路由器之间的延迟最小。

在弗洛伊德算法那一节里,我们提到过什么是最短路径问题,以及它的两种类别。假设在一个网络中有 10000 台计算机,它们彼此之间相互连接,如果我们采用弗洛伊德算法来解决互联网中路由的问题,就需要 Θ(n3), 也就是 1012 数量级的计算,以及 Θ(n2), 即 108 量级的内存空间,这种时间和空间的开销是任何路由器都不能承受的。另外,通常每台设备每次只对一台设备发送信息,而弗洛伊德算法计算的是所有节点之间的最短路径,而我们并不需要这么多。因此就有了单源最短路径问题,即计算某个节点到其他节点的最短路径。接下来,我们就来看看迪克斯特拉算法是如何解决这类问题的。
迪克斯特拉算法
假如我们有下面这样的一张图:
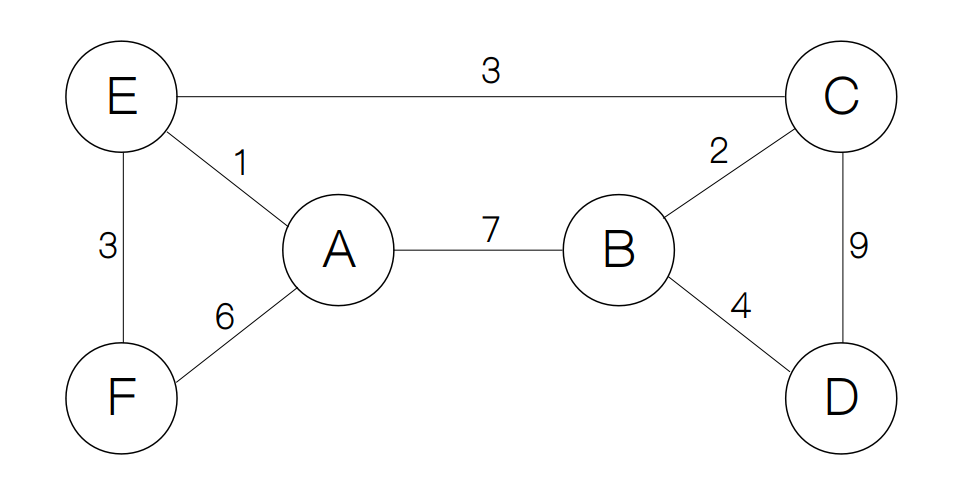
首先,对于单源最短路径问题而言,我们自然要选一个节点来作为源节点(source vertex),这里我们选择节点A,然后,我们对每一个节点分别用min_dis和parent来记录到源节点的最短距离和前驱节点(用于寻找最短路径)。在最开始,我们将源节点的min_dis初始化为 0,把其他节点初始化为 ∞。而将所有parent初始化为None。
class Vertex(object):
def __init__(self, name):
self.name = name
self.neighbours = []
self.visited = False
self.predecessor = None # 前驱节点
self.min_dis = inf

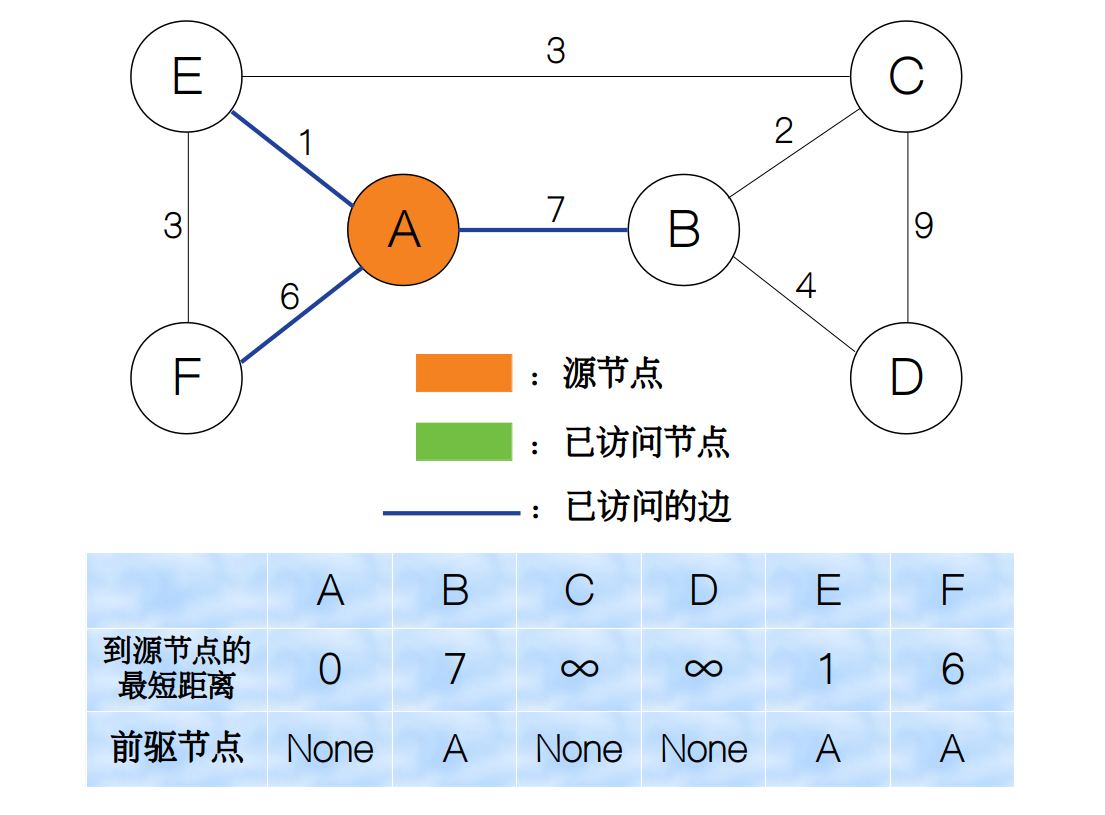
接下来我们要遍历与A相连的所有边,更新与之相连的所有节点的min_dis和predecessor,我们用u来表示当前节点,v表示相邻的节点,edge(u, v)来表示u和v相连的边。每一次遍历,我们都比较u.min_dis和edge(u, v) + v.min_dis的值,如果后者较小,我们就把v.min_dis更新为edge(u, v) + v.min_dis,并同时使v.predecessor = u。比如A到B的距离为 7,因为B.min_dis = ∞,A.min_dis + edge(A, B) = 7,所以我们需要更新更新B.min_dis和B.predecessor为 7 和 A,剩下的节点E和F也同样如此。
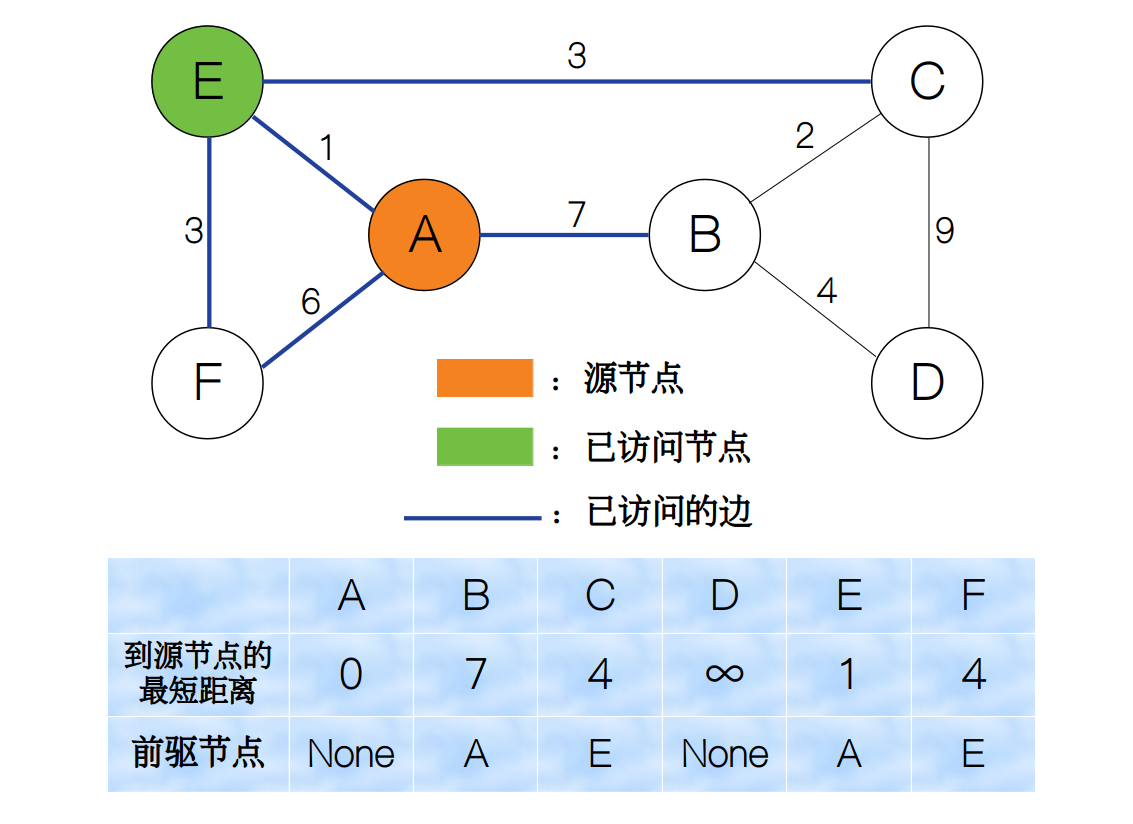
节点A被访问后,我们标记为visited。那么我们要怎样跳到下一个节点继续上述的过程呢?这里我们采用贪心策略,选择最小权值的边对应的节点来作为下一个节点。这里,我们选择节点E,然后再重复前面的步骤(更新节点参数,标记被访问,跳转到下个节点)即可。我们看到,节点F的最短距离从原来的 6 变为了 4,而前驱节点从原来的A变为了E。
我们一直重复上面的过程,直到所有节点均已被访问,我们将整个过程用一个动画来表示。
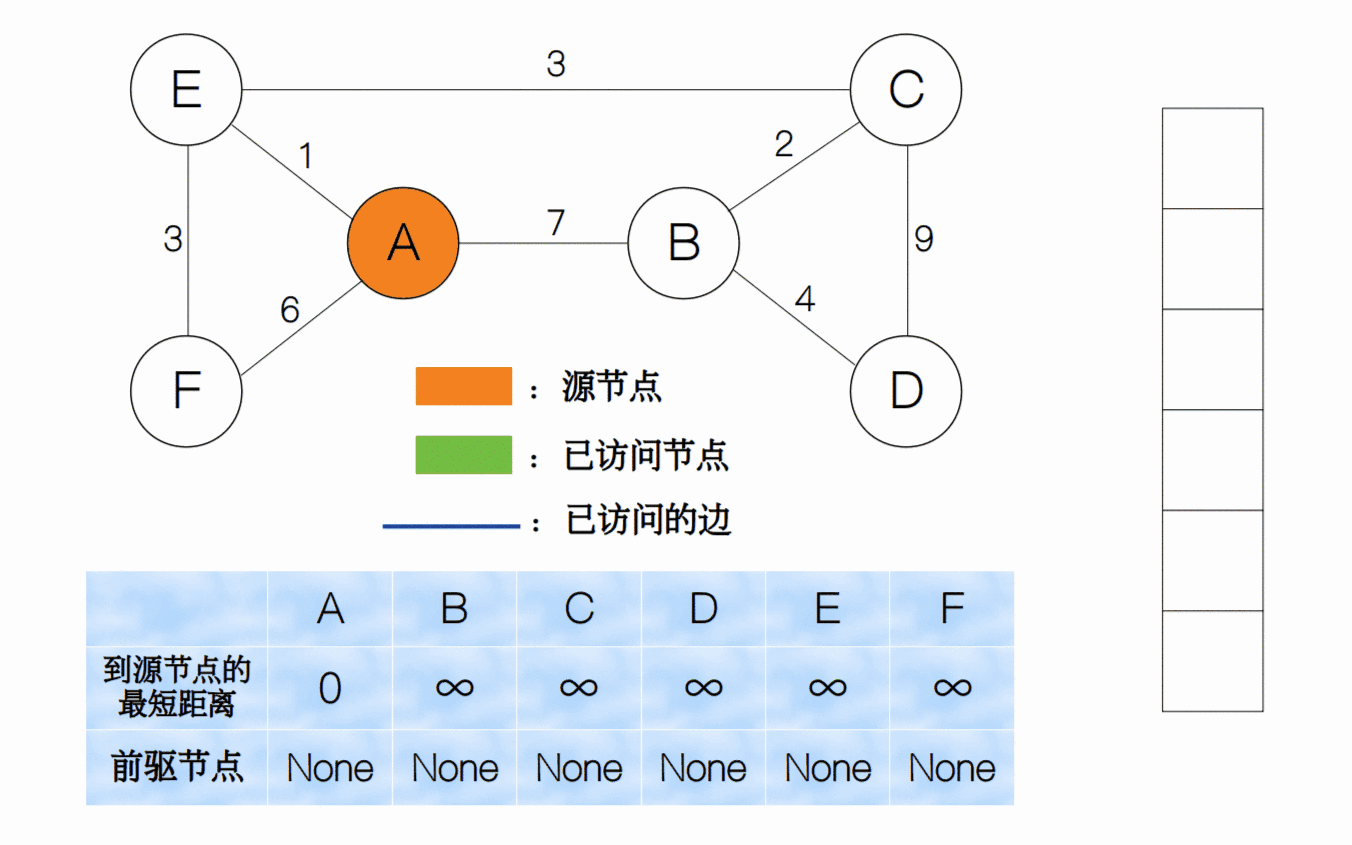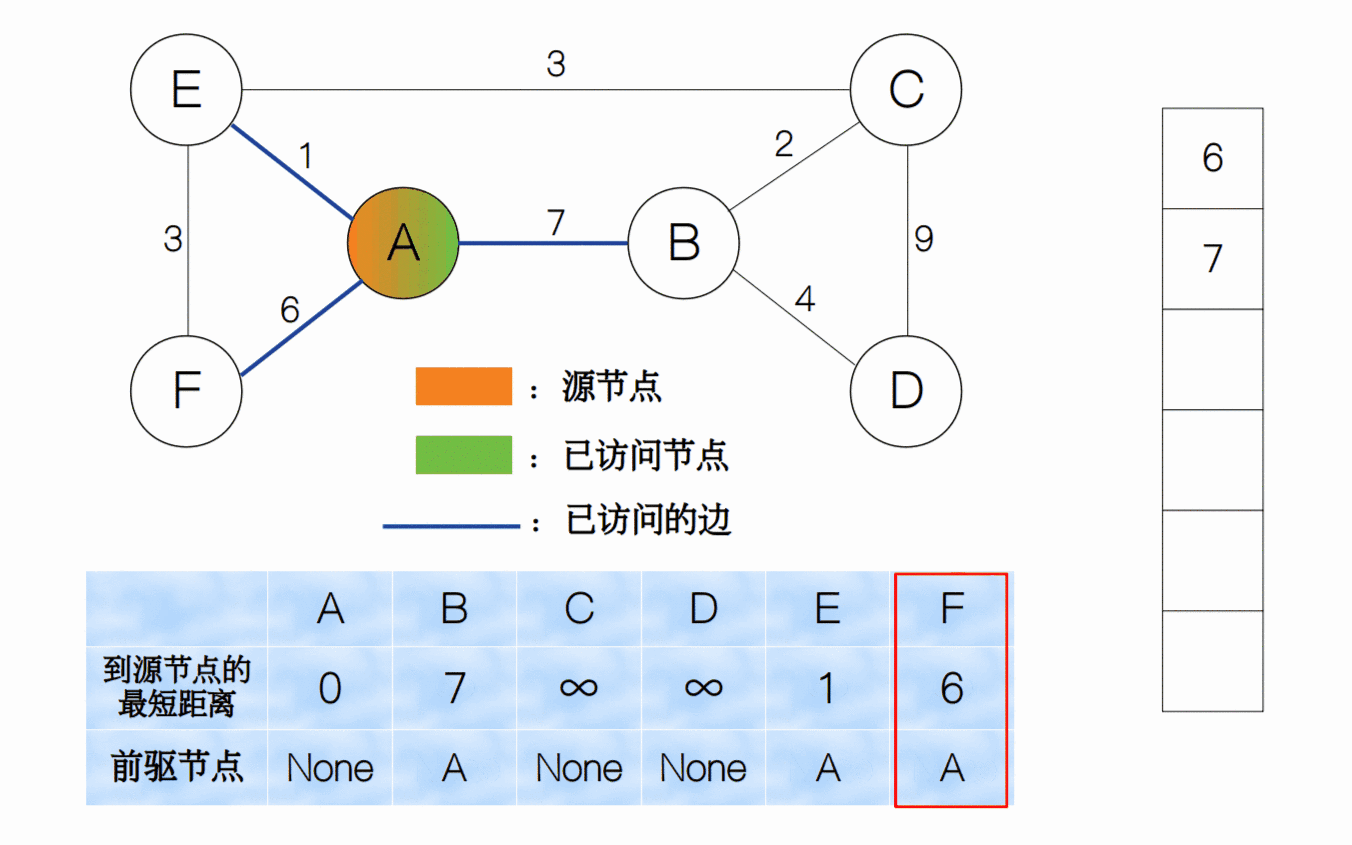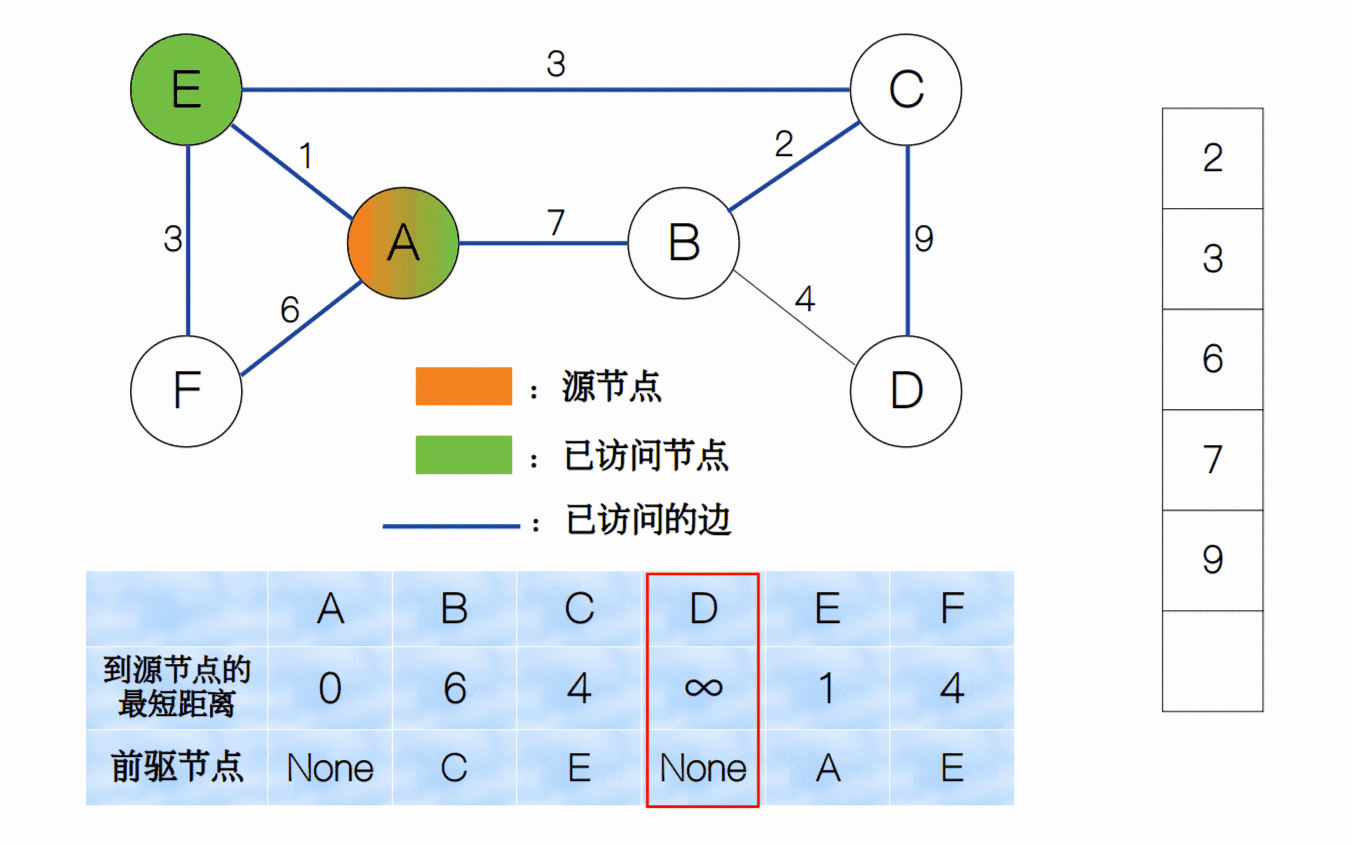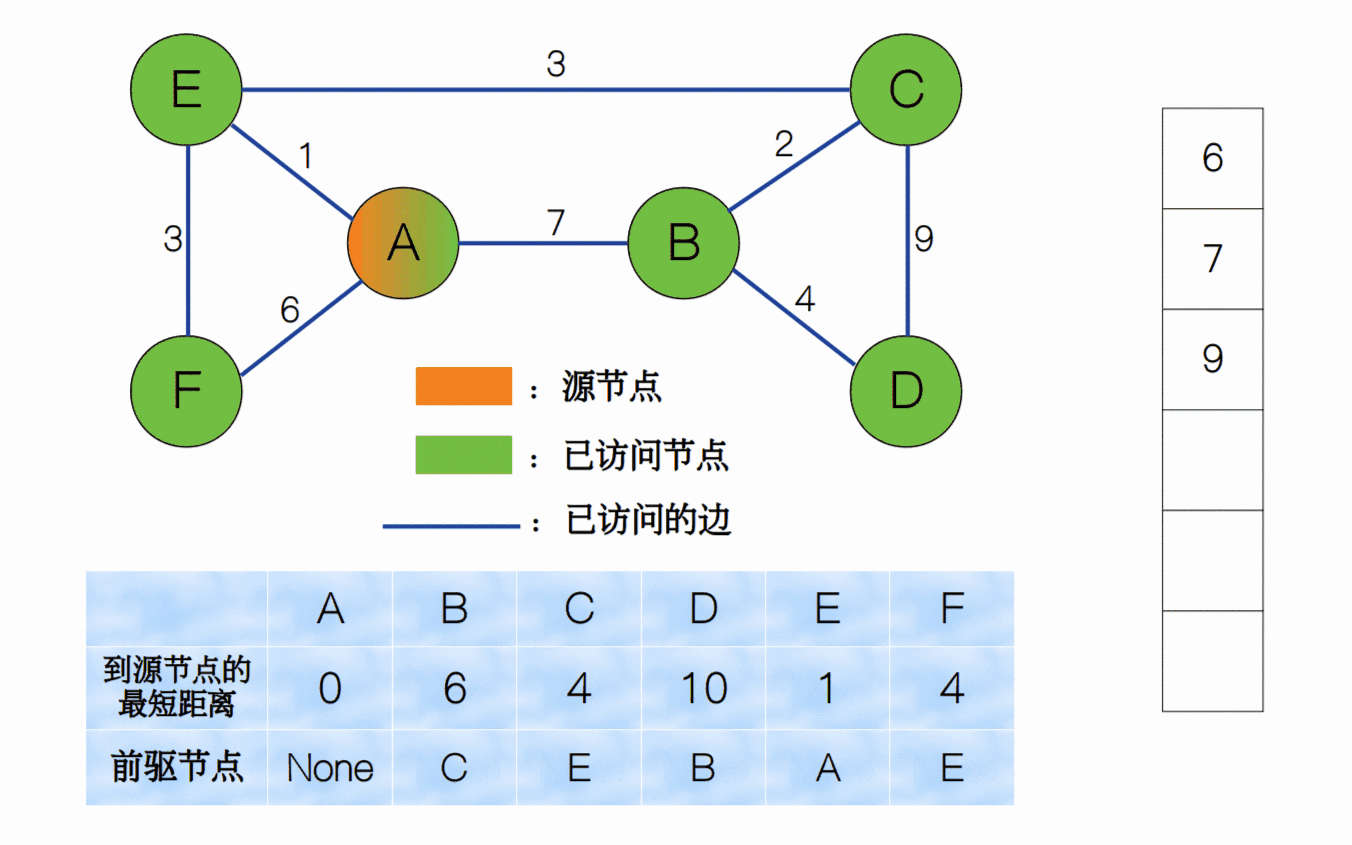
同样,我们可以用堆的数据结构来实现最小权值边的选择,每次有新的边被访问时我们就加入到堆中,并调整堆结构;而取最小权值边的过程就是删除堆顶元素的过程。因此下面的代码中,我们用fix_up和fix_down两个函数来分别实现。
def fix_up(queue):
temp_idx = len(queue) - 1
parent_idx = (temp_idx - 1) // 2
heap = False
while not heap and parent_idx >= 0:
# 判断是否满足堆的性质
if queue[temp_idx].weight < queue[parent_idx].weight:
queue[temp_idx], queue[parent_idx] = queue[parent_idx], queue[temp_idx]
else:
heap = True
# 更新索引值
temp_idx = parent_idx
parent_idx = (temp_idx - 1) // 2
def fix_down(queue):
temp_idx = 0; size = len(queue)
temp_ver = queue[temp_idx] # 暂存当前节点
heap = False
while not heap and 2 * temp_idx + 1 < size:
j = 2 * temp_idx + 1 # 左孩子的索引
# 右孩子存在
if j < size - 1:
# 比较两个节点的权重
if queue[j].weight > queue[j + 1].weight:
j = j + 1
# 判断是否满足堆的性质
if queue[j].weight >= temp_ver.weight:
heap = True
else:
queue[temp_idx] = queue[j]
temp_idx = j # 更新 temp_idx
queue[temp_idx] = temp_ver
接下来,我们用一个get_next_ver来实现给定边和当前节点,获取下一个节点的过程。
def get_next_ver(u, e):
if e.pre is u:
return e.next
return e.pre
最后一步就是迪克斯特拉算法的主函数了:
def Dijkstra(G, source):
V, _ = G # 从 G 中获取节点集合和边集合
v_set = V
pqueue = [] # 优先队列
source.visited = True; v_set.remove(source)
cur = source; cur.min_dis = 0 # 将源节点的`min_dis`初始化为 0
while v_set:
for e in cur.neighbours:
if not e.visited:
e.visited = True
pqueue.append(e) # 将 e 加入到堆
fix_up(pqueue)
temp = get_next_ver(cur, e)
# min(u.min_dis+edge(u, v), v.min_dis)
if cur.min_dis + e.weight < temp.min_dis:
temp.min_dis = cur.min_dis + e.weight
temp.predecessor = cur
pqueue[0], pqueue[-1] = pqueue[-1], pqueue[0]
temp = pqueue.pop() # 删除堆顶元素
fix_down(pqueue)
if not temp.pre.visited:
cur = temp.pre
elif not temp.next.visited:
cur = temp.next
else:
continue # 下一个节点已被访问
cur.visited = True
v_set.remove(cur)
为了获取最短路径,我们定义一个get_shortest_path方法。该方法首先创建一个空的列表path,然后从目标节点开始,不停地将v.parent放入到列表中,直到v.parent为源节点。
def get_shortest_path(v):
path=[]
while v is not None:
path.insert(0, v.name)
v = v.predecessor
return path
我们知道,每次调整堆结构的时间复杂度为 Θ(log|V|),而构建堆需要 |E| 次,删除堆顶元素至少需要 |V| - 1 次。所以,迪克斯特拉算法的时间复杂度为 Θ((|V| - 1 + |E|)log|V|)。
我们来验证一下算法的正确性。将目标节点设为C, D, F,最后的结果为:
>>> python Dijkstra.py
>>> 从 A 到 C 的最短路径为:
A->E->C
最短距离为 4
从 A 到 D 的最短路径为:
A->E->C->B->D
最短距离为 10
从 A 到 E 的最短路径为:
A->E->F
最短距离为 4
→ 本节全部代码 ←