字符编码
我们知道,计算机只能读懂由 0 和 1 构成的二进制编码。因此,我们每天看到的汉字或英文字符都会被编码成二进制的形式,如果你熟悉一些常用的编码方式,你会发现无论是 ASCII 码还是 Unicode,每个字符都占用都是等长的的编码位,也就是说,无论是 A, B, C, D 还是 + - × ÷,它们都是由等长的二进制来编码。

但这样的编码会出现一些问题,我们先假设 A, B, C, D, E 对应的编码分别为 000, 001, 010, 011, 100, 如果我们要对“ADCEBDABCCADEDBCACBD” 进行编码,得到的结果就是 000011010100001011000001010010000011100011001010000010001011,我们发现一些经常出现的字符,如 A 和 B 的编码长度始终是 3,对于这部分字符来讲,我们完全可以用更短的编码长度来进行编码,所以就有了变长的编码方式,而哈弗曼编码就是其中的一种。
哈弗曼树和哈弗曼编码
下面就来介绍一下哈弗曼树以及哈弗曼编码,它是由 David Huffman 提出的这种基于树形结构的编码方式,所以以他的名字来命名的。首先,我们将每一个符号(字符)用节点的形式来表示。每个节点包含了字符、出现的频率、对应编码、以及后面构建哈弗曼树时的左右孩子的信息。
class Node(object):
def __init__ (self, char, freq):
self.char = char # 字符
self.freq = freq # 频率
self.left = None # 节点的左孩子
self.right = None # 节点的右孩子
self.code = '' # 哈弗曼编码

我们用一个类HuffmanTree来表示哈弗曼树,首先需要做的是初始化字符串信息,以及每个字符和编码之间的映射关系。
class HuffmanTree(object):
def __init__ (self, string):
self.string = string
self.char2code = {} # 字符到编码的映射
self.code2char = {} # 编码到字符的映射
对于一个变长的编码而言,最重要的就是统计各个符号在字符串中出现的次数,次数越高的编码长度越短,次数越低的编码长度就越长,统计完成后我们将节点按照从小到大的方式排列。
def compute_freq(self):
string = self.string
char_freq = {}
for char in string:
char_freq[char] = char_freq.get(char, 0) + 1 # 计算每个字符出现的频率
return sorted(char_freq.items(), key=lambda x:x[1])

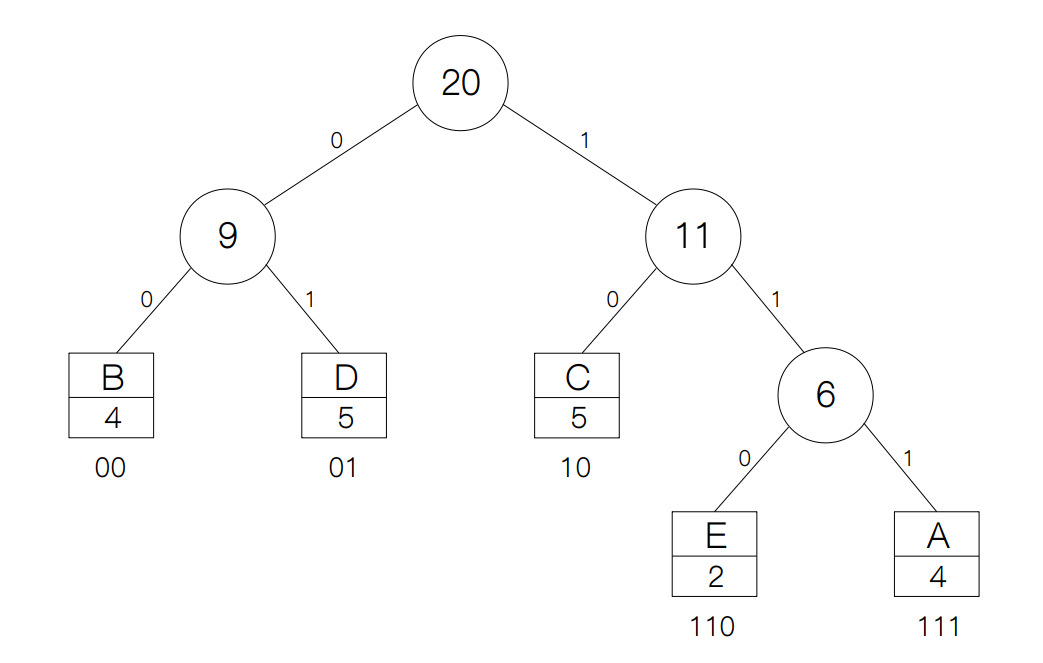
接下来,我们采用贪心的策略,选择频率最低的两个节点,这里选择 E 和 A,然后我们创建一个新节点,它的频率等于节点 E 和 A 之和,并且它的左右孩子分别指向 E 和 A。
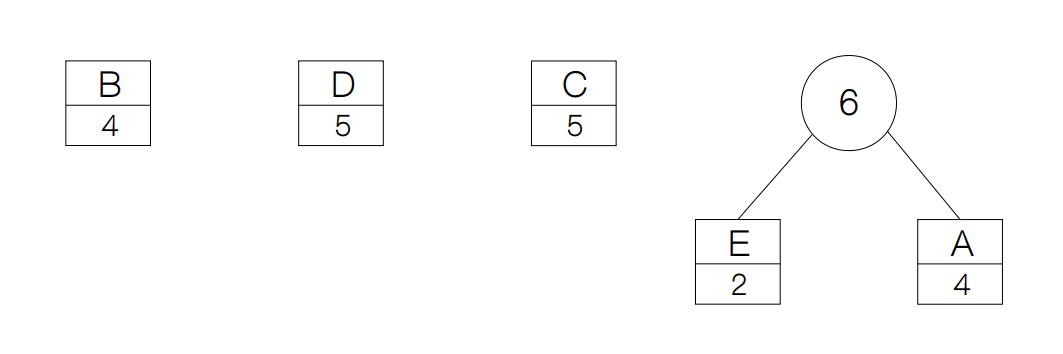
得到新节点之后,节点的频率分布就变成了{'B': 4, 'C': 5, 'D': 5, 'AE': 6},我们依然采用贪心的策略,再从中选择频率最小的两个节点,B 和 C,并构建新的节点。
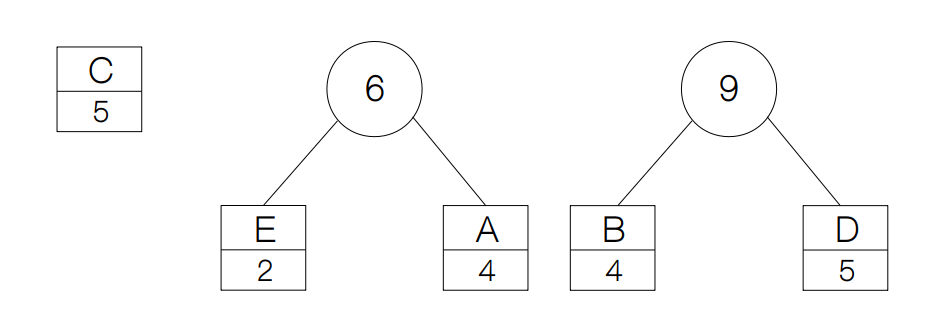
这样下来,节点的频率分布就变成了{'D': 5, 'AE': 6, 'BC': 9},于是我们还是重复上面的步骤,这一次我们选择节点 D 和 AE,并创建新节点,于是得到:
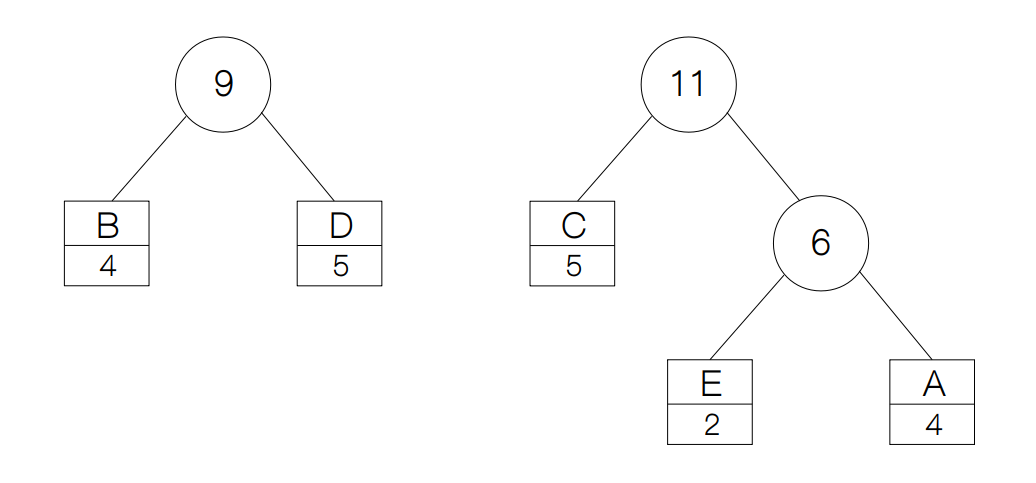
最后只剩下了 BC 和 ADE。用新节点将它们连接起来过后,我们就构建好了一棵哈弗曼树。
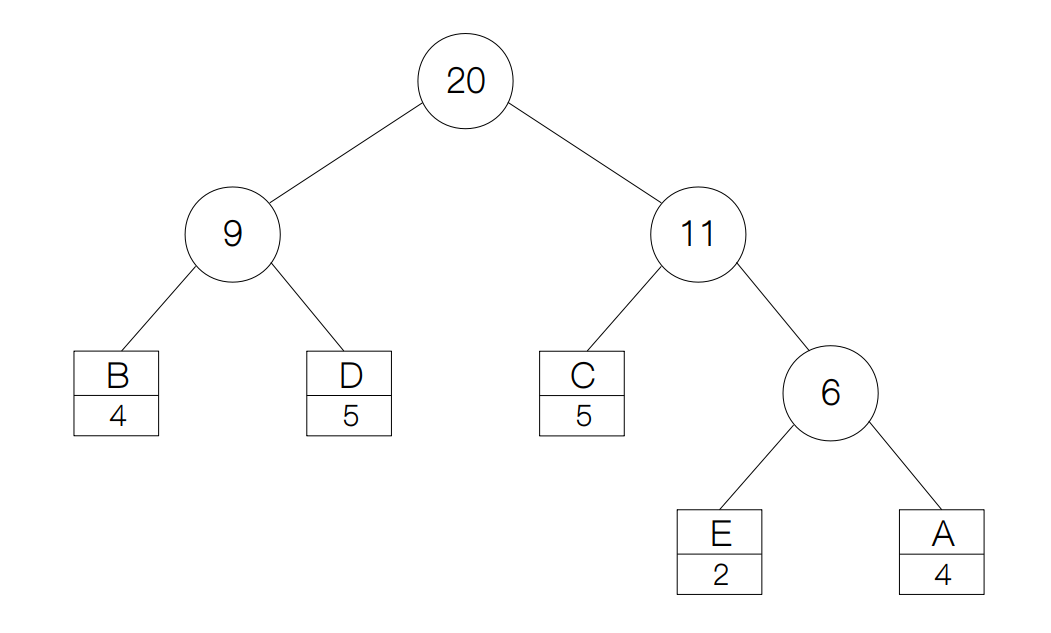
上述过程中涉及到了两个节点从队列中移除并创建新节点,因此,我们用一个类Queue来实现。
class Queue(object):
def __init__ (self):
self.queue = None # 用于保存节点
self.length = 0 # 队列的长度
def create(self, dict):
queue = []
# 入队
for char, freq in dict:
queue.append(Node(char, freq))
self.queue = queue
self.length = len(queue)
def add(self, node):
# 队列为空
if self.length == 0:
self.queue.append(node)
else:
# 将新节点插入到队列的相应位置
for i in range(self.length):
if self.queue[i].freq >= node.freq:
self.queue.insert(i+1, node)
break
# 插入到末尾
else:
self.queue.insert(self.length, node)
self.length += 1
def remove(self):
self.length -= 1
return self.queue.pop(0)
构建好哈弗曼树之后,我们需要将每个字符转换成相应的编码。哈弗曼编码的规则是,从树的根节点出发,我们规定每访问一个左孩子,就在节点的编码后面增加一个0,如果是右孩子就在后面增加一个1。于是我们访问每一个叶子节点,求出每个字符对应的编码,然后用char2code和code2char两个字典来分别储存它们之间的映射关系。
def build(self, queue):
while queue.length != 1:
u = queue.remove(); v = queue.remove()
w = Node(None, u.freq + v.freq) # 创建新节点 w ,其频率等于 u 和 v 频率之和
w.left = u; w.right = v # w 左右孩子指向 u 和 v
queue.add(w)
return queue.remove()
def map(self, root, x=''):
if root:
# 递归地访问节点
self.map(root.left, x+'0')
root.code = x
if root.char:
# 构建映射关系
self.char2code[root.char] = root.code
self.code2char[root.code] = root.char
self.map(root.right, x+'1')
最后,我们写出encode和decode函数来对字符串进行编码和解码。
def encode(self, string):
code = ''
for char in string:
code += self.char2code[char]
return code
def decode(self, code):
string = ''; pattern = ''
for c in code:
pattern += c
# 编码存在于字典中
if pattern in self.code2char:
string += self.code2char[pattern]
pattern = ''
return string
下面来运行一下程序,我们的字符串为ADCEBDABCCADEDBCACBD,运行后结果为:
>>> python Huffman.py
>>> 原字符串: ADCEBDABCCADEDBCACBD
每个字符的频率: [('E', 2), ('A', 4), ('B', 4), ('D', 5), ('C', 5)]
字符到编码的映射: {'B': '00', 'D': '01', 'C': '10', 'E': '110', 'A': '111'}
编码到字符的映射: {'00': 'B', '01': 'D', '10': 'C', '110': 'E', '111': 'A'}
编码后: 1110110110000111100101011101110010010111100001
解码后: ADCEBDABCCADEDBCACBD
我们看到,出现频率较高的 B, C, D 都是由两位二进制来编码,而较低的 A 和 E 则需要三位二进制来编码,这样我们在编码一个字符串的时候就会降低编码所占的储存空间,这也就是哈弗曼编码这么受欢迎的原因了。
→ 本节全部代码 ←