变治
变治(transform and conquer)也是一种解决问题的方式。用减治和分治解决问题时,我们只在原有问题的基础上求解,并没有对问题的实例做任何的变换,而变治法就是将实例从一种形式转换为另外一种形式的方法。这样听起来还是太抽象了,咱们还是拿一个具体的例子吧。
不知道大家有没有玩过一个叫做熄灯(英文叫 lights out)的游戏。规则很简单,以下面的图片(来源:维基百科)为例,面板上分布着 5 × 5 的格子,每个格子的对应一盏灯,且灯只有打开和熄灭两种状态。一开始所有的灯都是打开的,每按一次格子,当前的格子都会影响到该格子以及上、下、左、右四个相邻格子的灯的状态,即原来亮着的灯会熄灭,原来熄灭的灯会打开。游戏的目标是用最少的次数将面板上所有的灯都熄灭。
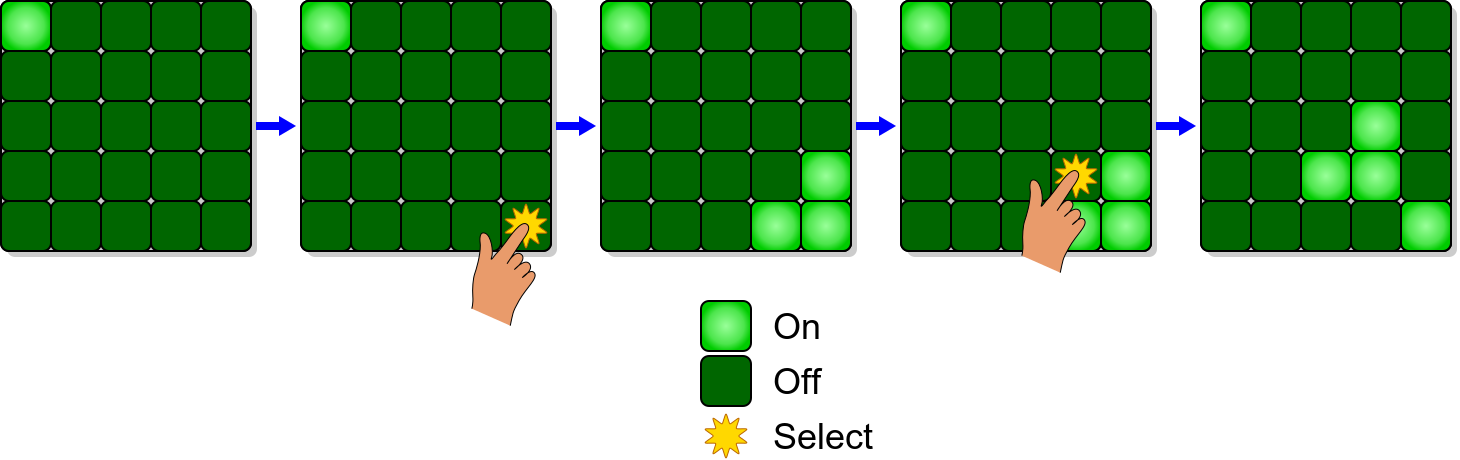
我们可以把面板上这些灯的状态抽象为一个 5 × 5 的矩阵,其中 1 表示打开的状态,0 表示熄灭的状态。现在,游戏的目标变为了怎样使全为 1 的矩阵变为全为 0 的矩阵。我们知道,对于每一个格子来讲,都有按下(1)和不按下(0)两种可能,所以对任意一个格子来讲,我们可以用一个方程来表示它的明暗状态:x1 ⊕ x2 ⊕ ··· ⊕ x25 ⊕ 1 = 0。方程的含义是怎样按这 25 个格子最后使得一个格子的状态为熄灭(0)。其中 ‘⊕’ 表示异或,它是一种逻辑运算,只有当 A 和 B 不相同时为 1,相同时为 0,因此恰好满足了游戏的规则。
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
因为每一个格子都会收到自身和相邻格子的影响,拿第一行第一列的格子来讲,它只会受到三个格子的影响,而其他格子不会对它造成任何影响,因此我们可以在每个 xi 的前面加一个系数 ai,受影响的为 1,不受影响的为 0。对于不受影响的格子来讲,无论 x 怎么变,其结果都为 0。如果对面板中每一个格子都列出相应方程式,我们就可以得到一个有 25 个等式 25 个未知数的方程组,如果用一个矩阵来表示其系数就是下面这样:

这样的矩阵我们可以采用用高斯消元法来解出每个 x 的值。但与一般的高斯消元不同的是,这里的运算符从 + 变成了 ⊕。具体的求解过程我们这里不再细究了,只想说明一点的是:原来的熄灯问题经过变换之后,变为了用高斯消元法求解线性方程组的问题,这就是变治法,这一章会我们会重点地讨论这个问题。
判断数组元素是否重复
先来举一个最简单的例子,判断数组元素是否有重复数。我们可以用最简单的方式:取数组的每一个元素,然后在剩余的数组元素里查看有没有重复。
def is_unique_bf(array):
length = len(array)
for i in range(length-1):
element = array[i]
for j in range(i+1, length):
if array[j] == element:
return False
return True
这样做效率很低,复杂度为 Θ(n2)。假设我们先将数组进行排序,因为对于一个有序数组,我们只需要查看一个元素跟它的下一个元素是否相等即可。因此我们的代码就可以改写为:
def is_unique_presort(array):
length = len(array)
array.sort() # 排序
for i in range(length-1):
if array[i] == array[i+1]:
return False
return True
由于算法由两部分构成(排序和主循环),所以该其复杂度也应该为两部分:Θ(nlog n) + Θ(n) = Θ(nlog n)。类似于这样的处理方式我们称为预排序(presorting)。
寻找众数
众数(mode)是一组数据中出现次数最多的数。如果用暴力求解的算法寻找众数,我们需要统计数据中所有数字出现的次数,然后选择出现频率最高的数。
def compute_mode_bf(array):
counter = {}
for i in range(len(array)):
counter[array[i]] = counter.get(array[i], 0) + 1
freq = 0
for key, value in counter.items():
if value > freq:
freq = value
mode = key
return mode
在最坏的情况下,数组里每一个元素出现的次数都为 1,所以第 i 个元素需要跟字典里的 i - 1 个元素进行比较,复杂度就为 Θ(n2)。
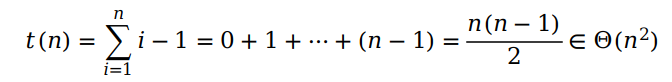
如果对数组进行预排序,我们用一个循环就可以找出数组的众数,因为相同的元素在有序数组里一定是相邻的。
def compute_mode_presort(array):
array.sort() # 排序
i = 0; freq = 0
while i < len(array):
temp_freq = 1; temp_mode = array[i]
while i + temp_freq < len(array) and array[i+temp_freq] == temp_mode:
temp_freq += 1
if temp_freq > freq:
freq = temp_freq; mode = temp_mode
i += temp_freq
return mode
上述的算法只需要遍历一次数组,再加上排序算法,故复杂度为 Θ(nlog n) + Θ(n) = Θ(nlog n)。
→ 本节全部代码 ←