最近点对问题
在前面的章节里,我们分别讨论了最近点对和凸包问题,但采用的都是暴力解法,即枚举出所有情况,因此算法的效率非常低。这节的内容,我们就来讨论一下如何用分治法来解决这两个问题。
既然是分治法,在解决最近点对问题的时候自然就离不开将这些散点进行分组,所以这里我们用一条垂直分界线 L,将散点分成两部分,SL 和 SR。

其中,SL 包含 ⌈n/2⌉ 个点,而 SR 包含 ⌊n/2⌋ 个点。
接下来,我们分别计算出左右两部分的最近点对距离 dL 和 dR。

然后我们取它们的最小值 d = min{dL, dR}。但是这里的 d 不一定就是全局的最小值,因为分别位于分界线 L 的左右两边的点可能存在更短的点对。因此,我们需要在分界线左右宽度均为 d 的区域内寻找出更短的点对。

在这个区域中,我们只需要把所有的点对全部列举出来,然后选择最小的那对,最后与前边计算得到的 d 进行比较取较小者即可。这里为了计算方便,我们可以先对这些区域内的点的 y 坐标进行排序,然后再逐个查看每个点对。这样做的好处是一旦我们发现点对的纵坐标之差 yi - yj 大于 d,我们就可以直接跳过这种情况,因为点对的距离 ((xi - xj) + (yi - yj))1/2 一定大于 yi - yj 的值,因此可以减少不必要的计算。
那么左右两半部分各自最近点对要怎样计算出来呢?我们可以用前面提到的方法,再将这些散点分为左右两部分,然后再分别做计算,像这样一直递归下去,直到当散点个数小于等于 3 个时,我们就用直接求解的方式将最近点对计算出来。

代码实现:
当 n <= 3 时:
def brute_force(x, y):
dmin = np.inf # 初始化 dmin 为无穷
for i in range(len(x)):
for j in range(i + 1, len(x)):
if (x[i] - x[j]) ** 2 + (y[i] - y[j]) ** 2 < dmin:
dmin = (x[i] - x[j]) ** 2 + (y[i] - y[j]) ** 2
coordinates = np.array([[x[i], y[i]], [x[j], y[j]]])
return dmin, coordinates
主函数cloest_pair_dc:
def closest_pair_dc(P, Q, n):
if n <= 3:
return brute_force(P, Q)
else:
left = (len(P) + 1) // 2; right = len(P) - left # 左右两部分的散点数
P_left = P[:left]; P_right = P[left:]
Q_left = Q[:left]; Q_right = Q[left:]
d_left, pair_left = closest_pair_dc(P_left, Q_left, left) # 从左半部分递归地寻找最近点对
d_right, pair_right = closest_pair_dc(P_right, Q_right, right) # 从右半部分递归地寻找最近点对
# 选择较短者
if d_left < d_right:
d = d_left; temp_pair = pair_left
else:
d = d_right; temp_pair = pair_right
m = P[(len(P)) // 2]
S = [] # 存储区域 |x - m| < d 内所有的点
for key in P:
if abs(key - m) < d:
S.append(key)
for i in range(len(S) - 1):
j = i + 1
while j < len(S) and (XY_pair[S[i]] - XY_pair[S[j]]) ** 2 < d:
if (S[i] - S[j]) ** 2 + (XY_pair[S[i]] - XY_pair[S[j]]) ** 2 < d:
d = (S[i] - S[j]) ** 2 + (XY_pair[S[i]] - XY_pair[S[j]]) ** 2 # 更新 d
temp_pair = np.array([[S[i], XY_pair[S[i]]], [S[j], XY_pair[S[j]]]]) # 更新点对
j += 1
return d, temp_pair
结合前面的讲解和代码,我们可以写出下面的递归关系式:
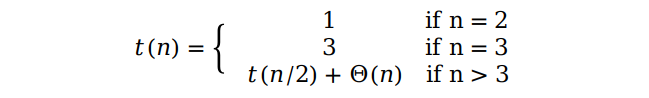
最后得到算法的复杂度为 Θ(nlog n)。我们发现比暴力求解算法的 Θ(n2) 有了明显的进步。
凸包问题
跟前面一样,用分治法解决凸包问题也需要将所有散点分为两部分,然后分别从这两部分中找出构成凸多边形的点。

具体步骤是分别选取横坐标中最小和最大的两个点 p1 和 pn,我们很容易证明 p1 和 pn 就是构成凸多边形的点,于是将这两个点连接起来构成向量 p1pn。现在问题就变为了从向量左右两侧的散点中分别找出构成凸包的点。

接下来我们需要从左右两侧的点中找出距离向量 p1pn 最远的点 pmax,该点即可作为构成凸多边形的点。

找出距离最远点其实就是使 △p1pmaxpn 的面积最大,如果你熟悉线性代数,计算三角形的面积即计算下面行列式的值。
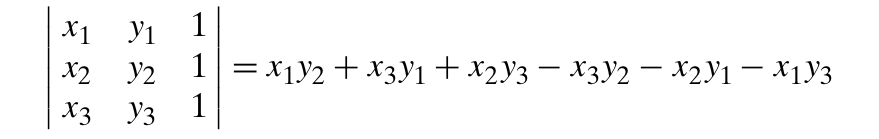
其中 (x1, y1), (x2, y2), (x3, y3) 分别表示 p1, pn 和 pmax 的横纵坐标。如果行列式为正,代表 pmax 的值在向量 p1pn 的左侧;如果为负值,则代表 pmax 在向量 p1pn。于是我们写出相应的代码:
def compute_area(x1, y1, x2, y2, x3, y3):
area = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3
return area
如果存在距离相同的点,我们选择使 ∠pmaxp1pn 最大的 pmax。
def compute_cos(x1, y1, x2, y2, x3, y3):
# 利用余弦定理计算角度
a = np.sqrt((y3 - y2)**2 + (x3 - x2)**2)
b = np.sqrt((y3 - y1)**2 + (x3 - x1)**2)
c = np.sqrt((y2 - y1)**2 + (x2 - x1)**2)
return -(b**2 + c**2 - a**2) / (2 * b * c)
寻找 pmax 的主函数:
def find_p_max(subset, p_left, p_right):
x1 = p_left[0]; y1 = p_left[1]
x2 = p_right[0]; y2 = p_right[1]
max_area = 0
for i in range(len(subset)):
x3 = subset[i][0]; y3 = subset[i][1]
area = compute_area(x1, y1, x2, y2, x3, y3)
if area > max_area:
max_area = area
angle = compute_cos(x1, y1, x2, y2, x3, y3)
idx = i
elif area == max_area:
# 如果面积相同,则选择使∠p_maxp1pn最大的p_max
cur_angle = compute_cos(x1, y1, x2, y2, x3, y3)
if cur_angle > angle:
angle = cur_angle
idx = i
return subset[idx]
我们从点集合subset中寻找距离向量最远的点。其中subset表示向量 p1pn 划分出的两部分点集合,我们用下面两个函数来生成它们:
def is_in_set(p, p_left, p_right):
# 去掉 p1 and pn
if p[0] == p_left[0] and p[1] == p_left[1] or p[0] == p_right[0] and p[1] == p_right[1]:
return False
return True
def generate_subset(totalset, p_left, p_right):
subset = np.array([[]])
x1 = p_left[0]; y1 = p_left[1]
x2 = p_right[0]; y2 = p_right[1]
for i in range(len(totalset)):
x3 = totalset[i][0]; y3 = totalset[i][1]
area = compute_area(x1, y1, x2, y2, x3, y3)
if area > 0 and is_in_set(totalset[i], p_left, p_right):
if subset.shape[1] == 0:
subset = np.append(subset, totalset[i][np.newaxis, :], axis=1)
else:
subset = np.append(subset, totalset[i][np.newaxis, :], axis=0)
return subset
找到 pmax 后,我们连接 p1pmax 和 pmaxpn(这里以上半部分的 pmax 为例)。此时,我们再从 p1pmax 和 pmaxpn 的左侧中分别寻找距离最远的点,来作为构成凸包的点。如果我们递归地执行上述的操作,所有构成凸包的点就都能够找到了。最后将这些得到的点首尾相连,就得到下面这张图啦~

因此,我们写出主函数 quick_hull。
def quick_hull(subset, p_left, p_right):
# subset 为空
if subset.shape[1] == 0:
return
p_max = find_p_max(subset, p_left, p_right)
global pairs # 用于存储构成凸包的点
pairs = np.append(pairs, p_max[np.newaxis, :], axis=0) # 增加一个维度
upper_subset = generate_subset(subset, p_left, p_max)
lower_subset = generate_subset(subset, p_max, p_right)
quick_hull(upper_subset, p_left, p_max)
quick_hull(lower_subset, p_max, p_right)
最后是我们的画图代码:
def plotting(hull_points, scatter_points):
upper_points = np.array(generate_subset(hull_points, hull_points[0], hull_points[1]))
lower_points = np.array(generate_subset(hull_points, hull_points[1], hull_points[0]))
x_upper = sorted(upper_points[:, 0])
x_lower = sorted(lower_points[:, 0], reverse=True)
x = [hull_points[0][0]]; x.extend(x_upper); x.append(hull_points[1][0]); x.extend(x_lower); x.append(hull_points[0][0])
y = []
for key in x:
y.append(XY_pair[key])
plt.scatter(scatter_points[:, 0], scatter_points[:, 1], s=15)
plt.plot(x, y, c='r')
plt.grid()
plt.show()
假设散点是随机分布在平面上,每次都要把点集划分为相等的两部分,所以每一次问题的规模都会减半。划分好以后,我们需要遍历整个点集,以寻找距离最远的点,这个过程是一个线性的复杂度。因而,我们可以写出下面的递归关系式:
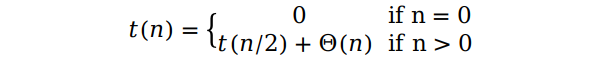
故平均复杂度为 Θ(nlog n)。
相比暴力求解的 Θ(n3) 复杂度,分治法解决凸包问题在效率上有了更明显的进步。
→ 本节全部代码 ←