图的两种遍历

邻接矩阵和邻接表

在讲数据结构的那一节里我们提到了图这种数据结构，并且介绍了两种用来表示图的方法：邻接矩阵和邻接表。接下来我们来分别看看它们是如何表示一张图的吧。

对于图而言，节点之间的连接是不受限制的，即一个节点可以连接任意节点（包括自身），并且还具有方向性。所以，我们可以用 0 和 1 两种状态来表示一个节点 u 是否能够连接到另一个节点 v。假设一个图由 n 个节点组成，那么我们就有 n² 种可能的连接。为了更直观地展现出来，我们用一个 n × n 的矩阵来表示：

根据上面的矩阵，我们可以得知节点 a 与节点 c 连接，而节点 d 却没有直接与节点 c 相连。如果我们将矩阵中的每一项都考虑在内，构建节点与节点的连接关系，并直观地展现出来就会和下面一样：

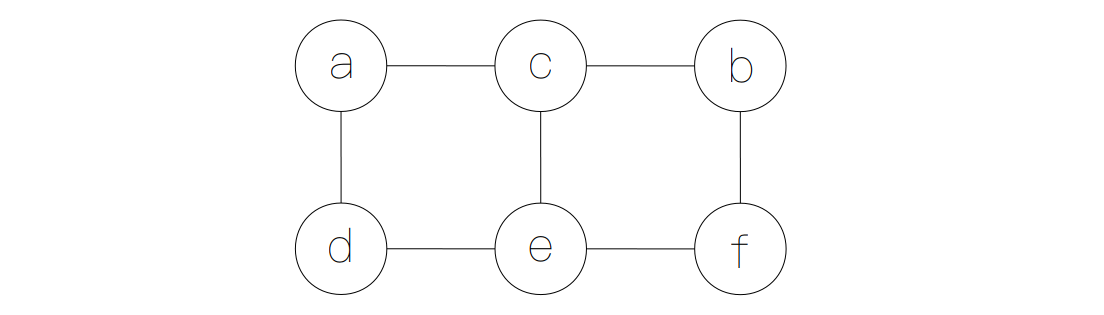
如果我们用一个链表的形式来表示一个节点到与之相连的全部节点，那么我们就可以得到一个由多个链表构成的数组。举个例子，上面的图中，节点 b 对应的链表中含有节点 c 和 f，说明节点 b 是直接连接到节点 c 和节点 f 的。同样，由于我们的图是一个无向图，所以节点 c 和节点 f 分别对应的链表也是含有节点 b 的。根据整个邻接表，我们也可以画出和上面一样的图。

深度优先遍历

在了解两种遍历算法之前，我们先要知道什么是遍历。遍历（traversal）是对树或图这种相对复杂的数据结构中的每一个节点进行逐一访问的过程。

先来介绍一下深度优先遍历（depth-first search），顾名思义它与深度有关系。其主要思想是：假设从一个节点出发，我们需要尽可能远地探索未访问的节点，直到不能继续探索为止，也就是遇到了“死胡同”（dead end），举个例子，我们要对下面的图进行遍历。

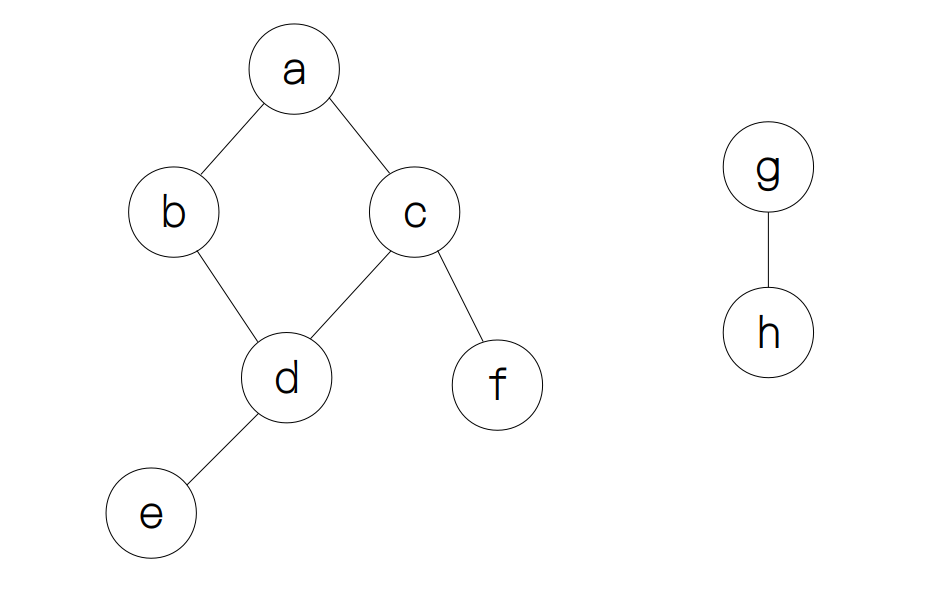
假设从节点 a 出发，我们首先将节点 a 标记为已访问。

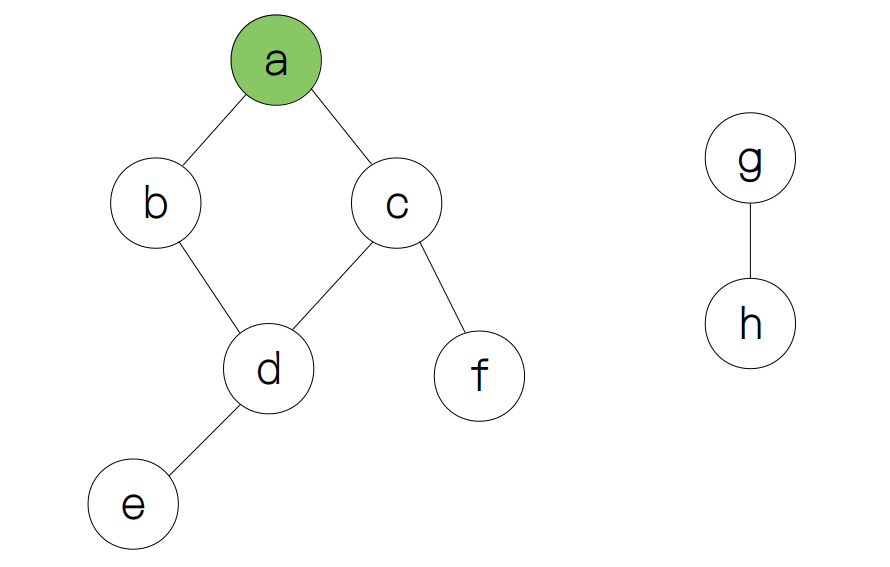
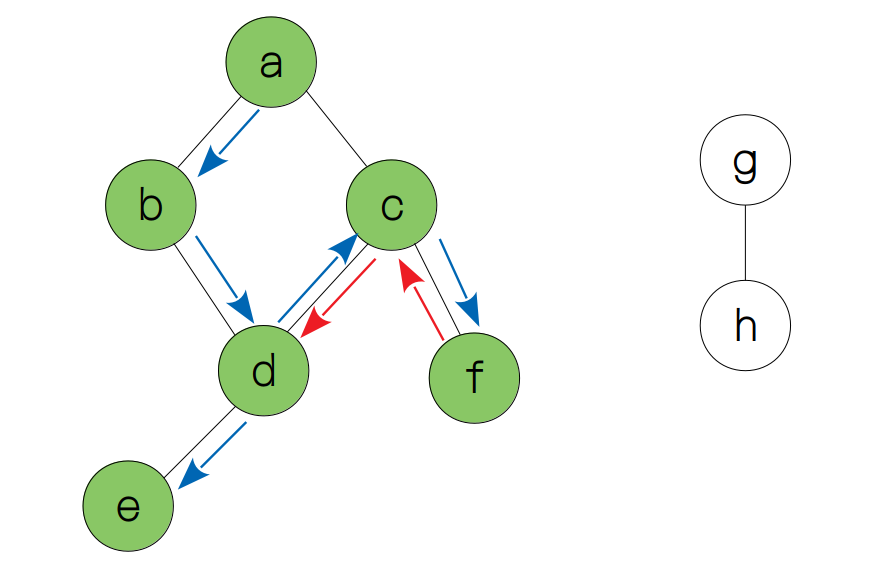
访问完节点 a 之后，我们要尽可能地远的探索其他节点，直到遇到“死胡同”。因此，在遇到“死胡同”之前，我们会访问节点 b, d, c, f (如出现分支则按照字母表顺序进行优先选择)。

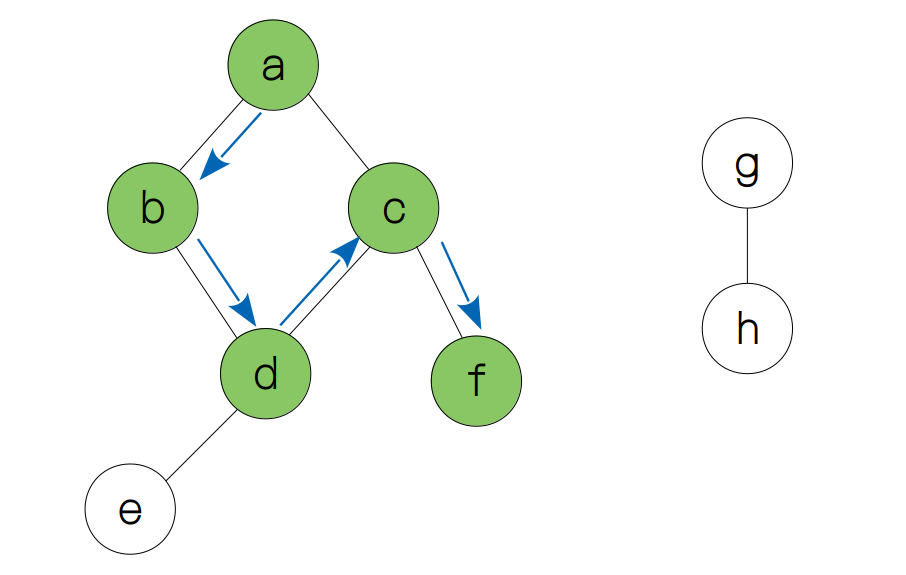
当节点 f 被访问后，我们需要先退回到节点 c，然后再继续探索，这时我们发现节点 c 已经没有可探索的节点了，因此我们要再退到节点 d，然后再尽可能地探索其他节点，直到再次遇到“死胡同”。因此节点 e 是下一个被访问的节点。

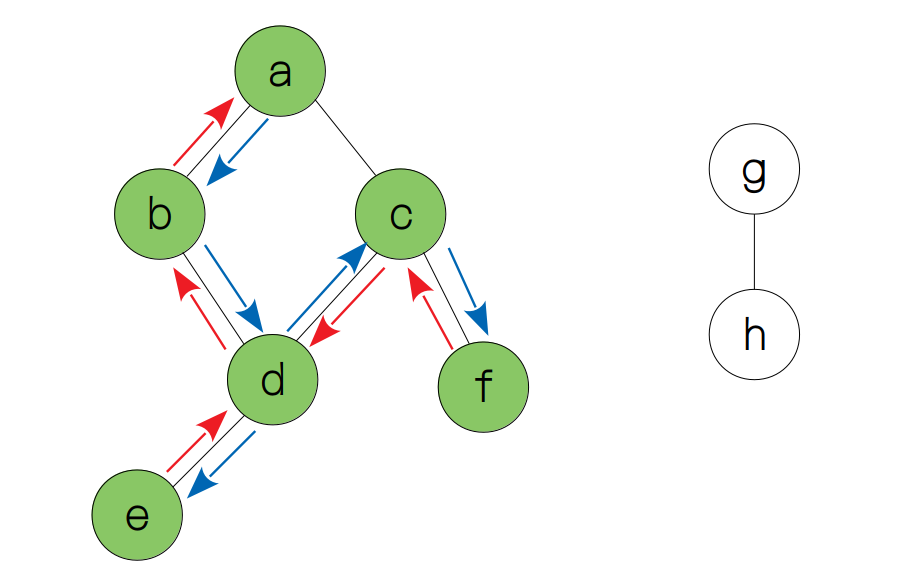
然后重复上述的过程，直到我们退回到了节点 a。

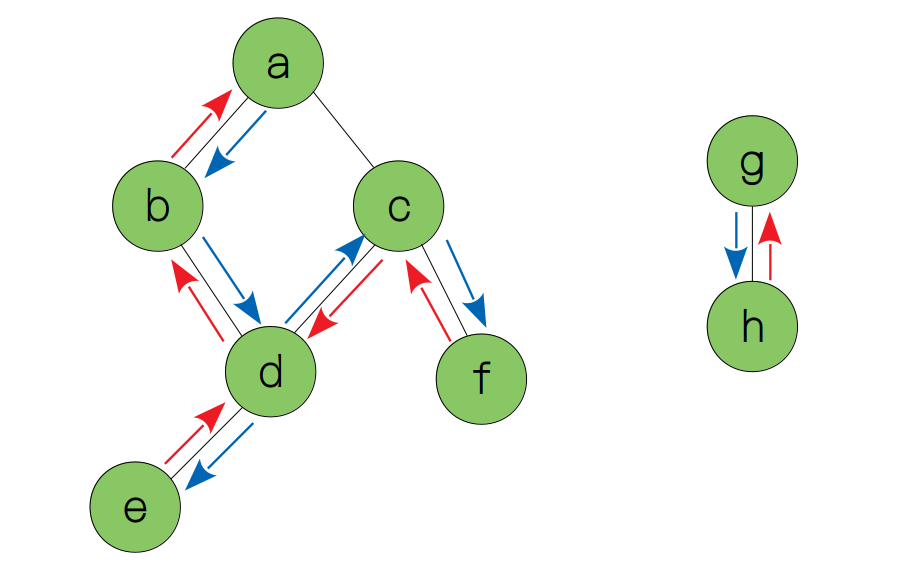
从上面的过程我们可以看出，深度优先遍历是需要用递归或者栈来实现的（因为后加入的节点要先离开），要实现这个代码，首先我们先要用一个类来表示图中的节点。

class Vertex(object):
    def __init__(self, value, visited):
        self.value = value
        self.visited = False
        self.neighbours = []  # 记录所有与之相邻的节点

然后实现一下深度优先遍历的过程：

def dfs(v):
    v.visited = True
    for w in v.neighbours:
        if not w.visited:
            w.visited = True
            dfs(w)

我们看到，由于节点 g 和节点 h 没有与左边的图连通，所以我们需要再构建一个函数用来遍历所有节点，来看这些节点是否被访问过，如果没有，我们就从该节点开始继续遍历。

def DFS(G):
    V = G.keys()
    for v in V:
        if not v.visited:
            dfs(v)

因此，我们要从节点 g 出发，再遍历剩下的节点，直到所有的节点都被遍历。

广度优先遍历

和深度优先遍历不同的是，广度优先遍历（breadth-first search）尽可能广地遍历其他邻近的节点，也就是节点是一层一层遍历的。

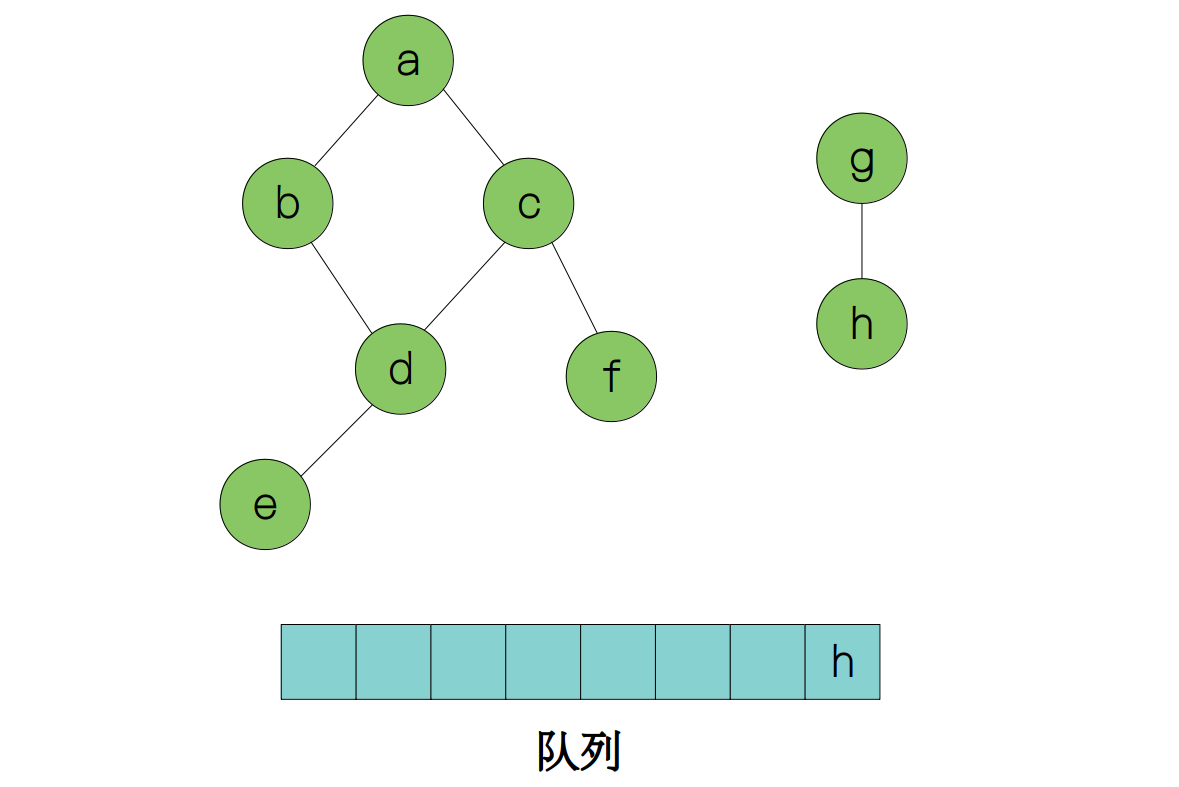
还是那上面的图为例，要实现广度优先遍历，需要用到队列这种数据结构。

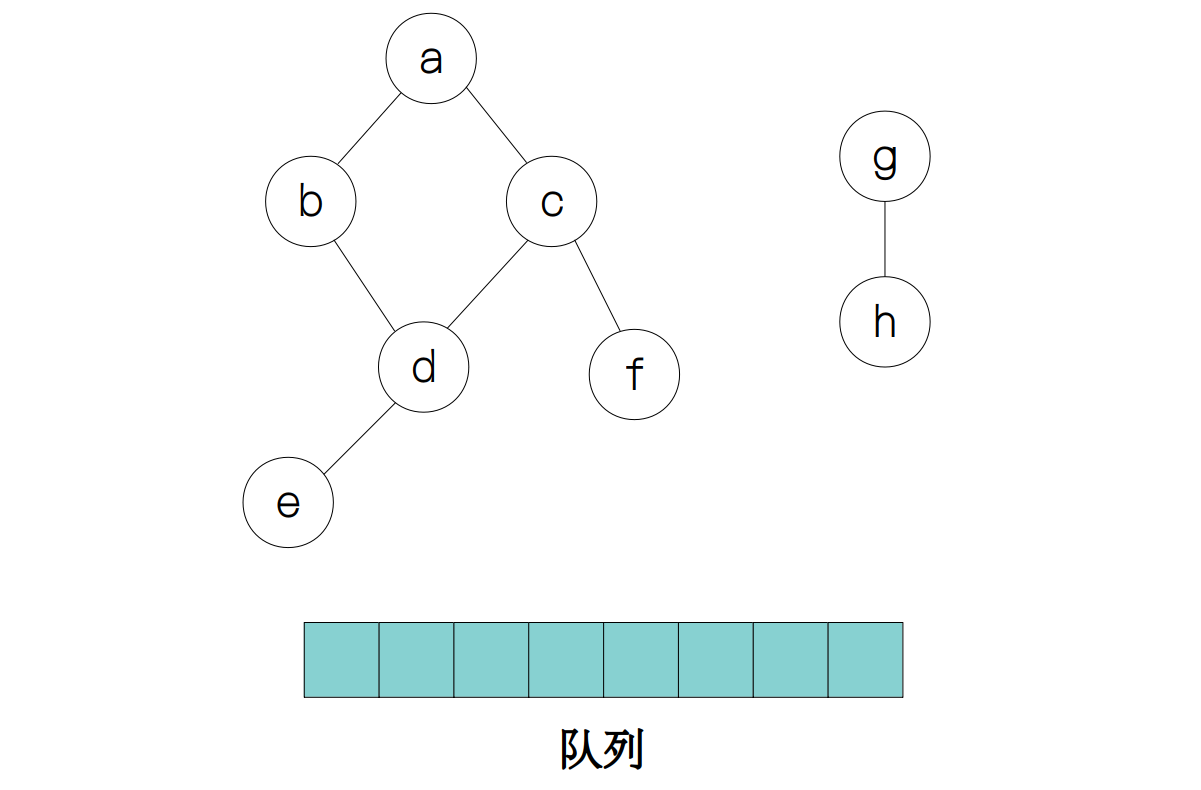
首先是节点 a 入队，并标记 a 已被访问。

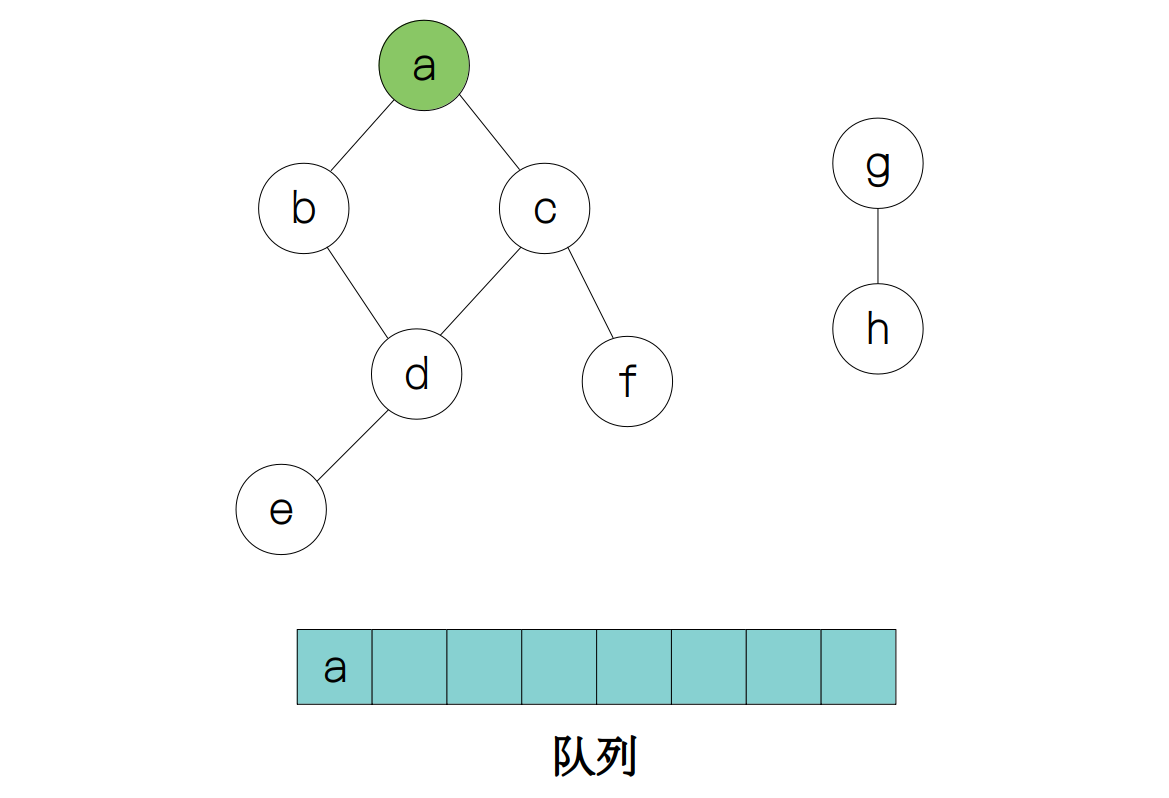
接下来访问 a 的相邻节点 b 和 c 入队，a 出队，同时标记节点 b 和 c 已被访问。

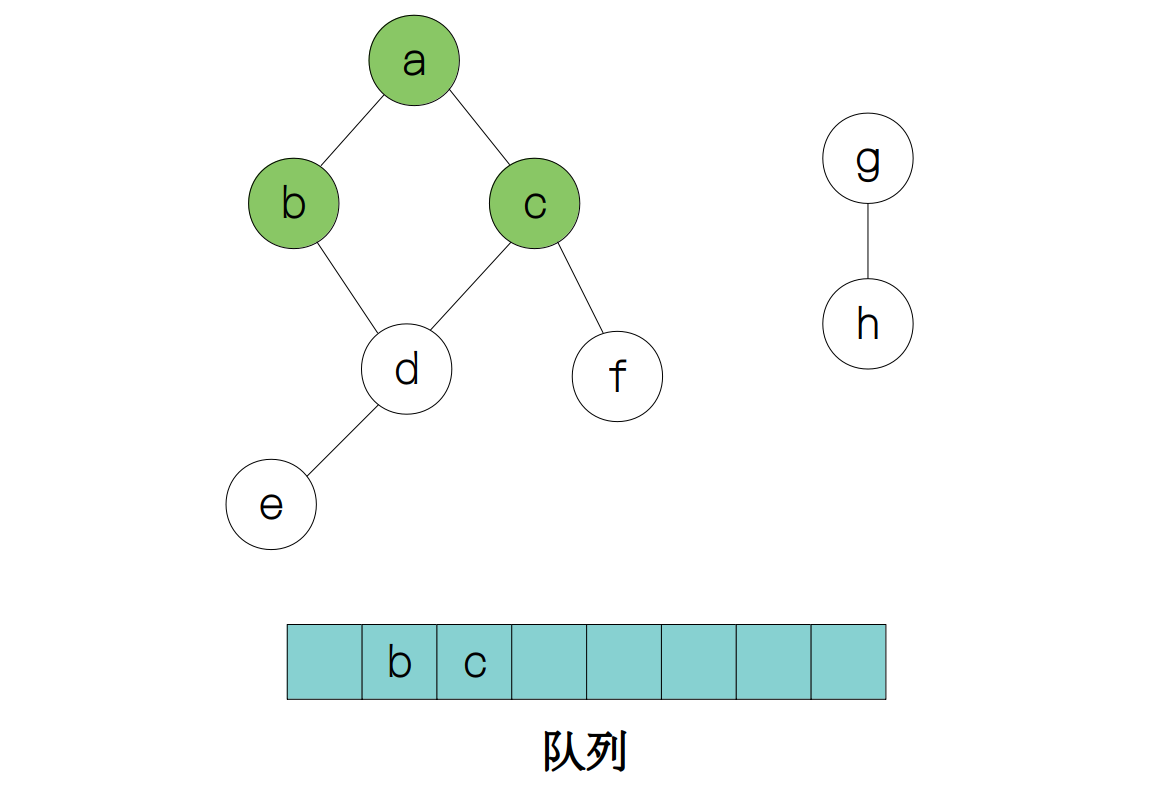
此时节点 a 的所有相邻节点全部被访问了，所以此时只需要考虑节点 b 和节点 c 的相邻节点，因此下一次被访问的节点就是 d 和 f，

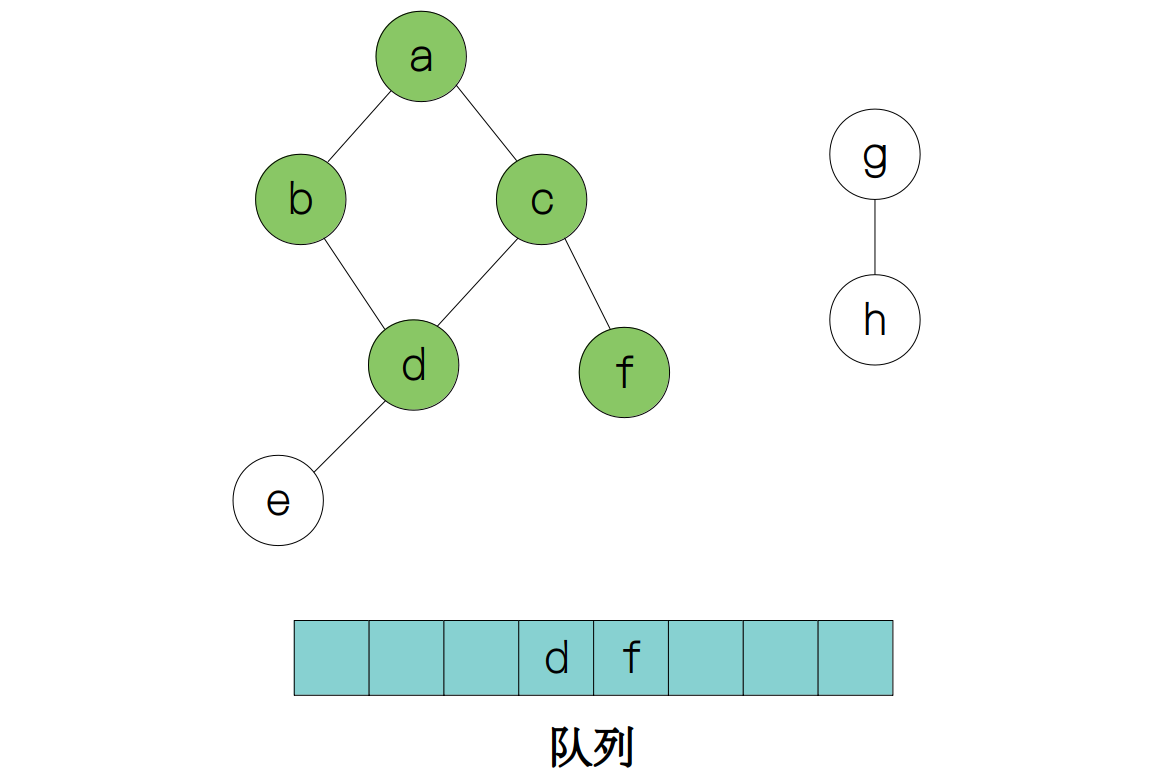
然后我们重复这个过程，最后得到：

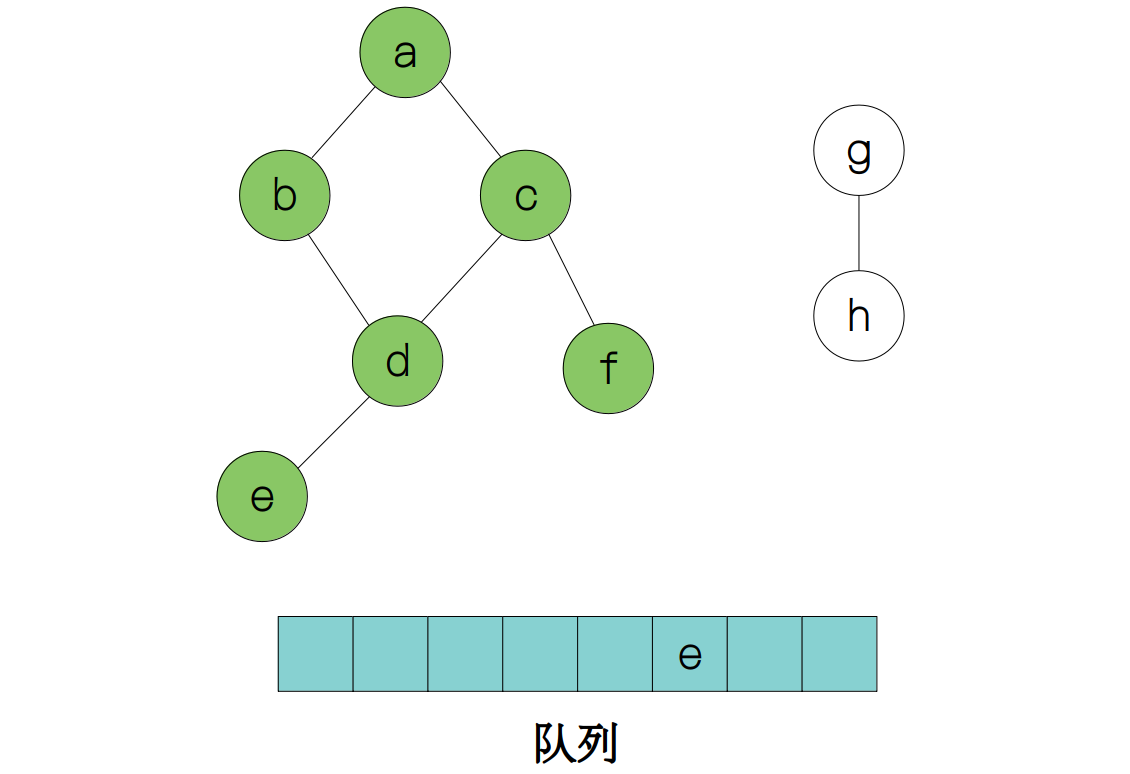
下面是代码实现过程：

def bfs(v):
    v.visted = True
    queue = []  # 初始化一个空队列
    queue.append(v)  # v 入队
    while queue:
        for w in v.neighbours:
            if not w.visited:
                w.visited = True
                queue.append(w)
        queue.pop(0)  # v 出队

同样，对于那些没有相互连接的图，我们处理的方式跟上面是一样的。

def BFS(G):
    V = G.keys()
    for v in V:
        if not v.visited:
            bfs(v)

因此我们要再从节点 g 开始，遍历剩下的图。

那么图的遍历跟暴力求解有什么关系呢？事实上，不管是深度优先遍历还是广度优先遍历，我们可以发现，每一个节点都执行了一次遍历算法，正是通过这种方式，才保证了图的每一个节点能够被访问，达到遍历的效果。后面我们讲到的暴力搜索也是同样的思想。

下面来谈谈遍历图的复杂度。我们知道图可以由邻接矩阵或邻接表来表示，因此我们要分别来讨论：

如果我们用邻接矩阵来表示，在执行遍历算法的过程中，由于每个节点都要查看其他节点是否与自己相连，即矩阵中每一行的 0 和 1，所以对于一个有 |V| 个节点的图来讲，就要查看 |V|² 次，其中 |V| 表示判断节点是否已经被访问过的次数。因而用邻接矩阵来表示的图的两种遍历的复杂度均为 Θ(|V|²)。

邻接表由于只记录了每个节点和与之相连节点的信息，即每条边的信息。所以在遍历的过程中，我们需要 |V| + |E| 次，其中 |E| 表示一个图里边的条数（具有两个方向的边算作两次）。因此用邻接表表示的图的两种遍历的复杂度均为 Θ(|V|+|E|)。

→ 本节全部代码 ←