最近点对问题
这一节内容,我们来看两个经典的几何学问题。首先是最近点对问题(closest-pair problem)。问题的描述是在一个二维平面上有一些随机分布的散点,要求我们在这些散点里找到两个点,使得它们的距离最小。
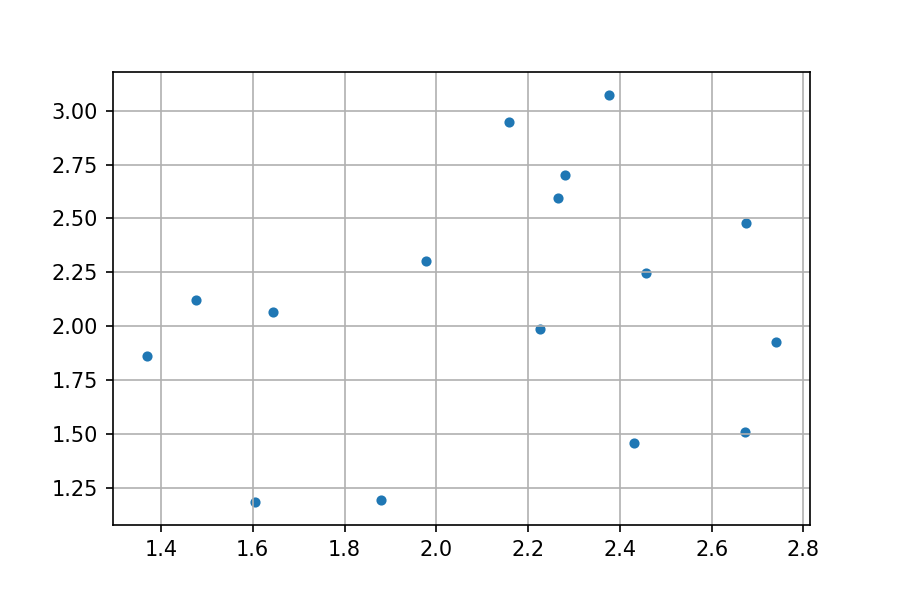
用暴力求解的方式解决这个问题很简单,只需要把所有的情况都列举出来,即计算出每一个点与其他所有节点的距离,然后取最小的值。如果平面上有 n 个点,那么要考虑的点对数就为 n(n-1)/2。比如下面的图中一共有 16 个点,我们就要考虑 120 种情况。
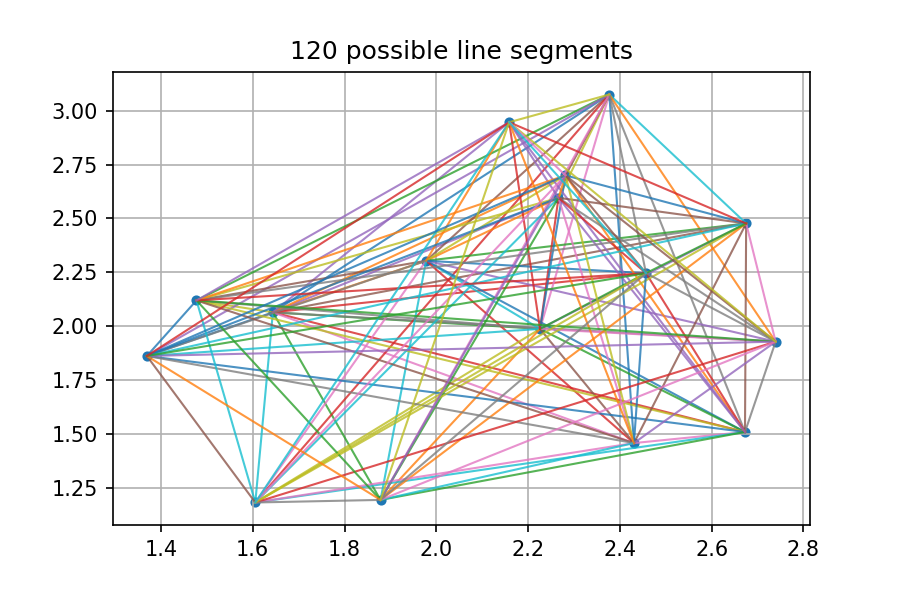
要实现这个过程也很容易,几行代码就可以搞定。
import numpy as np
def closest_pair_bf(X, Y):
d = np.inf # 初始化 d 为无穷
for i in range(len(X)-1):
for j in range(i+1, len(X)):
d = min((X[i] - X[j])**2 + (Y[i] - Y[j])**2)
return d
其中参数 X 和 Y 分别表示所有散点的横纵坐标的集合。在主程序中,我们用 numpy.random.normal 方法生成随机数,并且用np.column_stack方法将它们打包。
np.random.seed(13) # 为了代码的可复现性
X = np.random.normal(2, 0.5, size=[16, 1])
Y = np.random.normal(2, 0.5, size=[16, 1])
XY_pair = np.column_stack((X, Y))
最后将得到的最近点对在图中标注出来。

由于有两重循环,所以我们得到算法的时间复杂度为 Θ(n2)。
凸包问题
凸包问题(convex-hull problem)是这里我们要讨论的第二个问题。首先要弄明白什么是凸包,在生活中,你一定见过在一个扎满钉子的木头上套上一圈橡皮筋的场景,像下面这张图那样。哈哈,实际上橡皮筋围成的多边形就是一个凸包了。

从严格意义上来讲,凸包指的是由多个点构成的凸多边形(所有内角都小于180度),并且凸包还有一点性质是平面上所有的点都位于该多边形的内部。就像上面那张图中橡皮筋把所有钉子都围住一样。所以,我们要怎么来解决这个问题呢?答案当然还是采用最“暴力”的手段,穷举所有的情况,找到我们所需要的多边形。
从构成凸包的边中我们可以观察到,除了构成边本身的两个点以外,其他所有的点都位于边的同一侧。于是我们可以根据这个性质写出代码:
def convex_hull_bf(XY_pair):
pairs = [] # 用于存储满足条件的点
for i in range(len(XY_pair) - 1):
for j in range(i+1, len(XY_pair)):
a = XY_pair[j][1] - XY_pair[i][1]
b = XY_pair[i][0] - XY_pair[j][0]
c = XY_pair[i][0] * XY_pair[j][1] - XY_pair[i][1] * XY_pair[j][0]
k = 0; pos = 0; neg = 0 # pos 和 neg 用于统计直线左右两侧点的个数
while k < len(XY_pair):
if k != i and k != j:
if a * XY_pair[k][0] + b * XY_pair[k][1] - c > 0:
pos += 1
else:
neg += 1
if pos != 0 and neg != 0:
break
k += 1
else:
pairs.append((XY_pair[i], XY_pair[j]))
return pairs
对于判断一个点是在一条直线的左侧还是右侧,我们会用到了下面的公式:
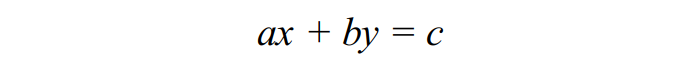
其中 a = y2 - y1, b = x1 - x2, c = x1y2 - y1x2,构成边的两个点的坐标分别为 (x1, y1), (x2, y2),而 x 和 y 分别待判定的点。如果值大于 0,说明该点在直线的左侧;如果小于 0,说明该点在直线的右侧。
最后我们将满足条件的点通过收尾相连的方式显示出来,这样我们就能画出多边形了。
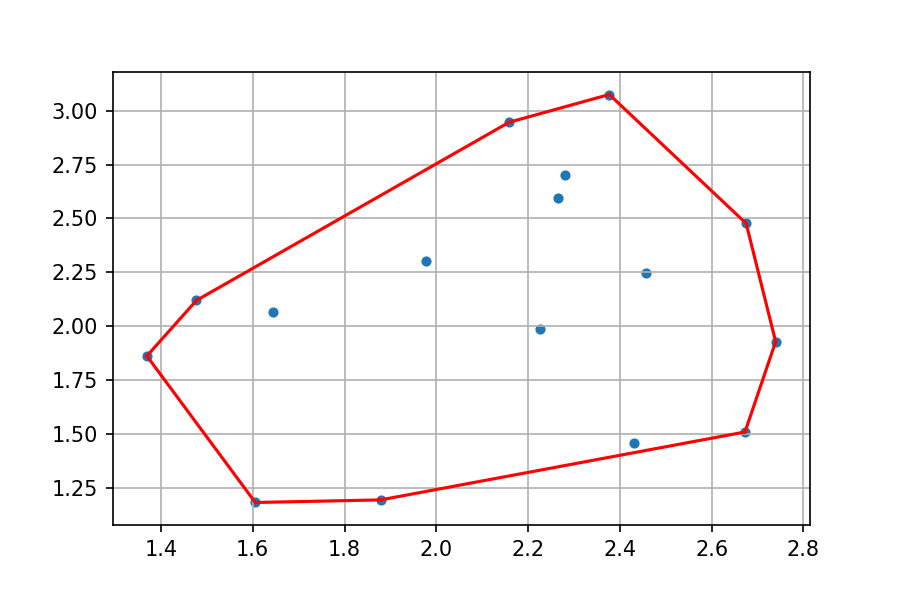
作图的代码如下:
def plotting(xy_pair, polygon):
plt.scatter(xy_pair[:, 0], xy_pair[:, 1], s=15)
for i in range(len(polygon)):
np_point_stack = np.stack(polygon[i], axis=1) # 将每一个点对打包成 (xi, yi) 的形式
plt.plot(np_point_stack[0], np_point_stack[1], c='r')
plt.show()
最后来分析一下复杂度。我们知道,如果平面上有 n 个点,那么一共就有 n(n-1) / 2 个点对,也就是直线的条数。对于每一条直线,又要从剩下 n - 2 个点中判断是否在直线的同一侧。这样一来,只要我们列出求和公式,再经过推导就能够得到复杂度为 Θ(n3),具体推导过程如下:
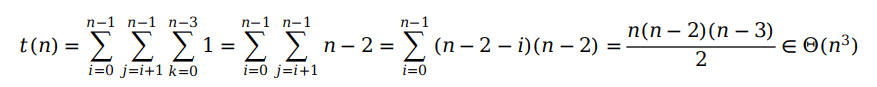
总结
我们可以看到,用暴力求解的方式解决这两个几何问题非常简单,但效率却是低,都是平方级和立方级的复杂度,所以这两种算法也只能解决小规模的问题。面对 n > 106 这种大规模的问题时,我们就要求助其他算法了。
→ 本节全部代码 ←