千禧问题
今天我们来说一个计算机领域里的一个超级难题,P 是否等于 NP。早在 2000 年 5 月的时候,Clay Institute 将这个问题列为了数学里的七大千禧问题之一,如果有人能证明出 P = NP 或 P ≠ NP,就会获得该机构整整 100 万美元的奖金。并且一旦证明出 P = NP 将会改变现有人类所有的知识体系,这个我们在后面的部分再详细地讨论,下面我们就来看看这个问题到底在讲什么吧。

P 问题与 NP 问题
首先我们要知道什么是 P 问题和 NP 问题,所谓的 P 问题就是能够在多项式的时间复杂度内解决的问题,这里的 P 指的是多项式时间(polynomial time)的意思,就是像 Θ(n), Θ(n2), ···, Θ(nk) 一样的能够用多项式表达出来的时间复杂度。我们在前面学到的算法大多数都可以写成这样的形式,比如排序问题,二分查找,图的遍历,最小生成树等。
对于那些不能在多项式的时间复杂度内解决的问题,比如说背包问题,分配问题等等,我们会认为这个问题很难,可能需要在指数或阶乘的时间复杂度内解决,但是如果我们能够在多项式的时间复杂度内验证一个答案是否正确,我们就把这类问题称为 NP 问题,其中 NP 表示不确定的多项式时间(non-deterministic polynomial time)。简单来说就是解决 NP 问题很难,但验证它却很容易。打个比方,数独是一个解决起来比较难的问题,但是如果我们往格子里随机填一些数字,然后验证它是否满足数独的规则就会比较容易。因此,这类问题也是科学家们最关心的问题。
多项式规约
既然 NP 问题都是比较难的问题,那么是否存在一个 NP 问题,使得所有 NP 问题可以通过多项式规约(polynomially reducible)得到它?这里的多项式规约指的是问题 A 的所有实例都能够在多项式的时间复杂度内转化为问题 B 的所有实例。规约后,如果问题依然是一个 NP 问题,我们就把它称作 NP-complete 问题;相反如果不是一个 NP 问题,我们称它为 NP-hard 问题。
举个例子,一元一次方程和一元二次方程的问题都是 NP 问题,因为我们可以选取一个 x 值,然后代入验证是否满足方程。我们发现,一元一次方程的问题可以规约成一元二次方程的问题,规约的过程很简单,只需要将 x 二次项系数改为 0 即可。而且一元二次方程有求根公式,所以对于一元一次方程而言,我们也可以代入到求根公式中得到方程的解。因此,我们可以说只要能解决一元二次方程,便可以解决一元一次方程,因为后者可以规约到前者。
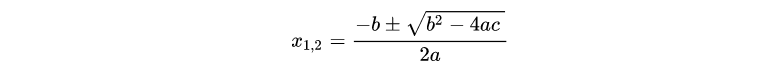
P = NP ?
那么问题来了,规约过后的 NP 问题能否在多项式的复杂度内解决呢?换句话说,P 问题和 NP 问题是否等价。如果 P = NP 就意味着任何能够在多项式的复杂度验证的问题也能够在多项式的复杂度解决它。反之则不成立,下图表示了 P, NP, NP-complete 和 NP-hard 之间的关系。

问题的意义
那就要小伙伴要说了,这个问题太深奥了,跟我们这种普通人没有关系呀。正是这个超级难的问题,还没有人证明出来,才保证了我们普通人的正常生活,因为很多关于密码学的问题都是基于 P ≠ NP 来的,正是基于这种假设才使我们的各种加密算法暂时不能被轻易的破解。所以,如果证明了 P ≠ NP 还好说,也就印证了一部分科学家的假设,一旦证明出 P = NP,那将可能会导致一些颠覆性的变化。
首先来说说它的好处,因为 NP 问题大多数都是不能够在多项式的复杂度内解决的,所以一旦 P = NP,我们就可以将任何一个 NP 问题转化为一个 P 问题。因此,一些现在看起来很难的问题都能够轻松的解决它,比如围棋有了终极解,生物领域中可以轻松破解遗传密码来任意操纵基因序列,很多数学猜想能够用计算机来演算推导,大量难题被解决等等,这些都是一些好的方面。
但是也会带来很多负面的影响,比如数学家会失业,关于复杂度的研究将会彻底失去意义,前面得到的成果将成为一纸空文。同时,P 如果等于 NP 会导致所有加密算法彻底失效,你的银行卡,手机密码,社交账号变得不再安全,黑客能够轻松进入你的电脑,比特币,区块链这些近年来很火的概念将会成为无人问津的领域,这样的例子还有很多很多。总之,证明出 P = NP 将会给我们的生活带来很大的变化。
上面的内容参考了知乎上的一篇文章得到。下面来谈一谈自己的观点吧,个人比较倾向于 P ≠ NP,因为 NP 问题很多都是指数级或更高的复杂度,要想把所有的 NP 问题都统一成 P 问题实属不易,但一旦证明出有一个 NP 问题不可能在多项式的复杂度内解决,那么 P ≠ NP 就成立了,而且证明出 P ≠ NP 比证明出 P = NP 对整个人类知识体系的影响力要小。所以,我更倾向于 P ≠ NP。