优先队列
在学习堆和堆排序之前,我们需要了解什么是优先队列。乘坐飞机前你一定清楚这样一个场景,在候机厅排队登机时,我们会看到有专门的头等舱通道,持有头等舱机票的乘客可以不用排队就能直接登机,就好像他们有“特权”一样。

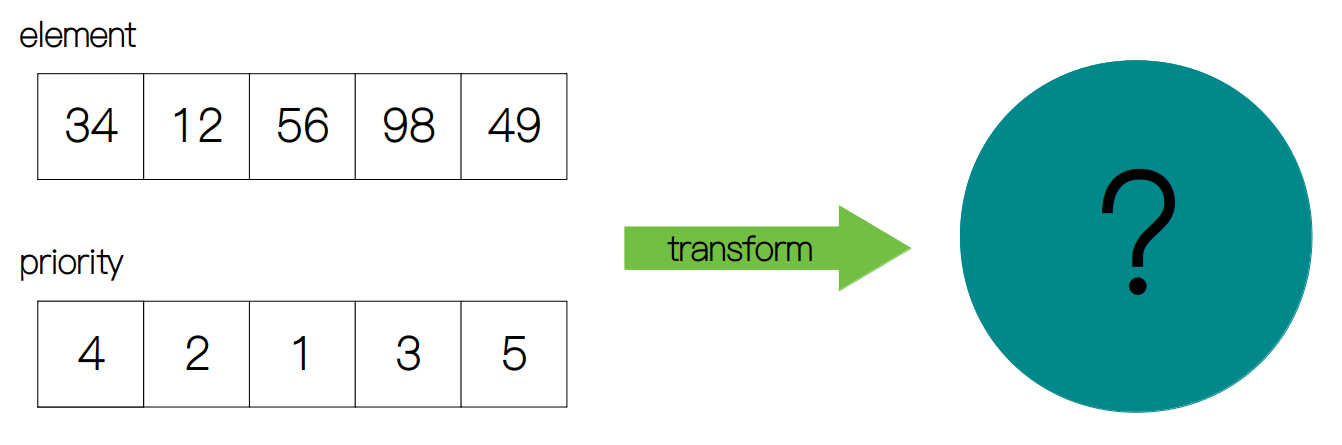
我们可以认为,坐头等舱的乘客的优先级比坐普通经济舱的乘客要高。如果用计算机里的队列来描述的话,头等舱的乘客在出队时总是先于经济舱的乘客。于是,我们可以定义出一种新的抽象数据类型,优先队列(priority queue),即所有元素都按照优先级的大小出队。举个例子,假设一个数组为 [34, 12, 56, 98, 49],优先级的顺序为 [4, 2, 1, 3, 5],那么出队的顺序就为 56→12→98→34→49。
堆
假设一个优先队列全由数字组成时,我们需要两个数组,一个用于存储数据,一个用于存储每个元素的优先级。所需要的存储量是普通数组的两倍,这显然是不可行的。另外,因为队列的出队操作只能严格地在队尾执行,所以每次出队的过程中,出队的元素必须要和队尾元素进行交换,然后再出队,并且每次出队后存储优先级的数组也要做出相应的变化才能够保证优先队列的性质,所以操作会非常麻烦。因此,我们还需要另寻他法,使优先队列的数据结构在操作上更简单。
我们可以借助二叉树的性质,将优先级越高的元素放置在越靠近根节点的位置,换句话说就是位于层数越低的地方。堆(heap)就是一种将优先队列变换为了二叉树的数据结构。下面来介绍一下它的性质:
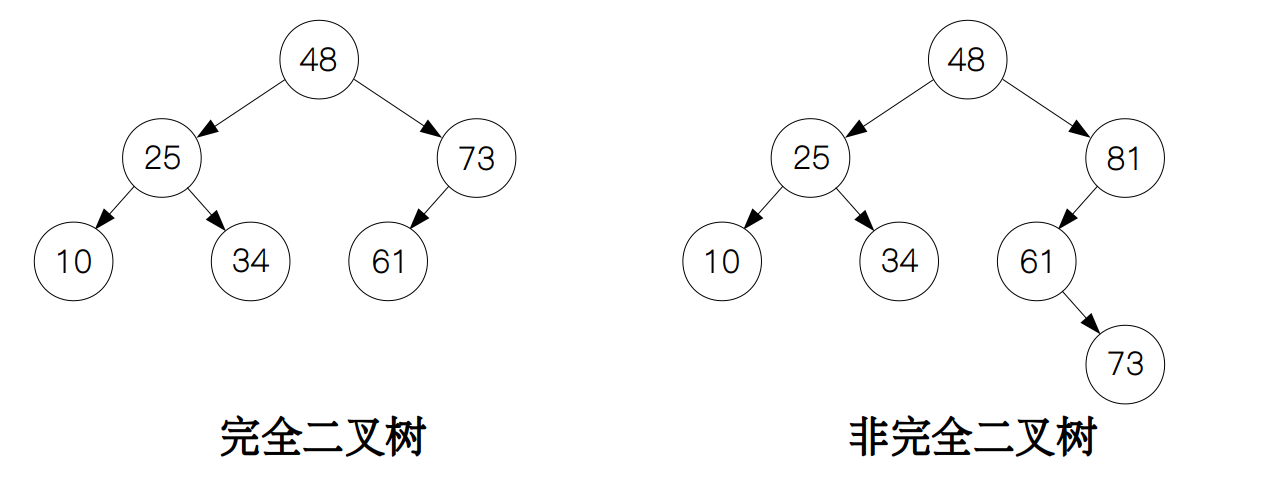
完全二叉树
堆是一棵完全二叉树。在数据结构那一节里,我们简单地提到了它。区分完全二叉树和非完全二叉树在于完全二叉树除了最后一层的节点没有排满以外,其他所有层均已排满。并且在构建完全二叉树的时候,新加入的节点在最后一层从左往右依次排列,直到排满为止。
堆的构建
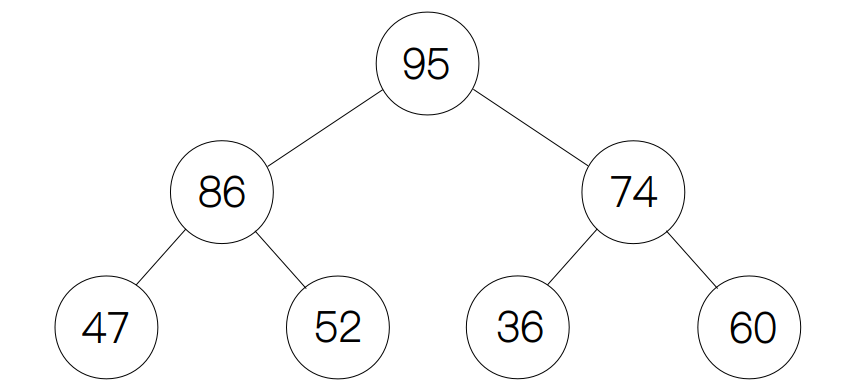
下面来说一说如何构建一个堆,如果数字越大的优先级越高,我们把这种堆称为大顶堆(max heap),数字越小,优先级越大的堆叫做小顶堆(min heap),这里以大顶堆为例,由于优先级越高的元素放置在越靠近根节点的位置,所以我们定义,所有父节点的值均大于等于其孩子节点的值,而孩子节点之间的大小我们不做要求,因此在大顶堆中根节点的值一定是最大值。例如下图中根节点 95 是最大值,它大于它的两个孩子节点 86 和 74,而节点 86 又大于节点 47 和 52。
有了堆的性质,下面我们就来构建一个堆。首先将数组元素以二叉树的形式表示出来,然后不断调整堆内元素的排列,直到满足堆的性质。
构建堆的具体过程在下面的视频中已经显示出来。具体来说就是先从最后一个具有孩子节点的父节点(节点 36)开始,然后选孩子节点较大的节点(节点 72),并与父节点比较大小。如果该节点比父节点要大,说明不满足堆的性质,因此就要交换这两个节点的值。交换后,被交换的父节点又与它的孩子节点进行比较,如果不满足堆的性质就交换两个节点的值,满足就完成当前循环,如此往复直到父节点没有子节点为止。对上述所有的父节点,我们都执行一遍比较操作,最后就能构建出一个堆了。
如果用数组来体现这一性质,那么数组元素就应该满足:ei ≥ e2i+1 并且 ei ≥ e2i+2。其中 ei 代表第 i 个元素的值。那么 i 的取值如何呢?假设数组中有 n 个元素,i 就从 ⌊(n-2)/2⌋ 开始递减到 0。
因此我们写出构建堆的代码:
def heaplify(array, temp_idx, size):
temp_val = array[temp_idx]
heap = False
while not heap and 2 * temp_idx + 1 < size:
j = 2 * temp_idx + 1 # 左孩子的索引
# 右孩子存在
if j < size - 1:
# 比较两个孩子的值
if array[j] < array[j+1]:
j = j + 1
# 判断是否满足堆的性质
if array[j] <= temp_val:
heap = True
else:
array[temp_idx] = array[j]
temp_idx = j # 更新 temp_idx
array[temp_idx] = temp_val
return array
在主程序中用一个for循环来控制调整堆的次数。
for i in range((len(array)-2)//2, -1, -1):
arrary = heaplify(array, i, len(array))
最后来分析一下构建堆的时间复杂度。假设堆有 h 层,且每一层均已填满。在构建时,我们需要从第 h - 1 层开始调整堆的结构,直到调整到堆的第 1 层。在最坏的情况下,第 i 层的元素最多需要比较 2(h - i) 次,而每一层最多有 2i-1 个节点,所以用一个求和公式来表示就是这样的:
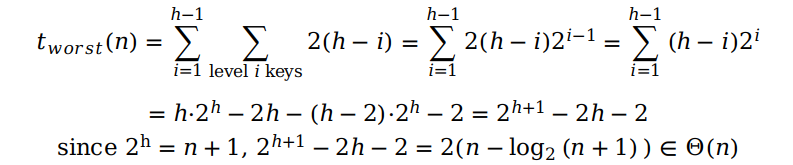
最后求得复杂度为 Θ(n)。
堆的删除
与普通队列一样,堆的删除只能在一侧(堆顶)进行。为了删除堆顶后仍能保持堆的性质,我们实际的操作是交换堆尾和堆顶的值,然后删除堆尾,最后堆顶元素从上到下调整堆的结构,如果不满足堆的性质就交换两个节点的值,满足性质后便不再调整。
上面的动画(来源于网络)展示了删除堆顶元素 95 的全过程。首先需要堆尾元素 60 交换位置,然后删除 95,最后从上到下调整节点 60 的位置。
在最坏的情况下,堆删除的复杂度取决于堆的层数 h。如果堆内有 n 个元素,那么堆的层数 h = ⌊log2n⌋ + 1,故复杂度为 Θ(log n)。
堆排序
堆排序(heap sort)是基于堆的一种排序,整个过程分为四步:
- 第一步:构建堆
- 第二步:堆顶和堆尾的值交换顺序,并删除交换后的堆尾元素
- 第三步:调整堆结构
- 第四步:重复第二步和第三步,直到堆为空
事实上,我们利用了堆顶元素在堆中总是为最大值的性质,然后取出最大值,同时调整堆的结构使得下一个堆顶元素又是堆的最大值,如果一直重复这个过程,数组就从大到小依次排列了。下面给出了堆排序的代码:
def heap_sort(array):
for i in range((len(array)-2)//2, -1, -1):
array = heaplify(array, i, len(array))
for i in range(len(array)-1, -1, -1):
array[0], array[i] = array[i], array[0] # 堆顶元素和堆的最后一个元素交换
array = heaplify(array, 0, i)
return array
我们再用一个动画(来源于网络)来感受一下堆排序的整个过程。
堆排序结合了构建堆和删除堆顶元素两个过程。构建堆的过程我们知道是一个 Θ(n) 的复杂度;删除堆的操作一共需要执行 n 次,而每次的删除操作复杂度均取决于当前堆的层数,所以我们需要列出下面的关系式来计算它:
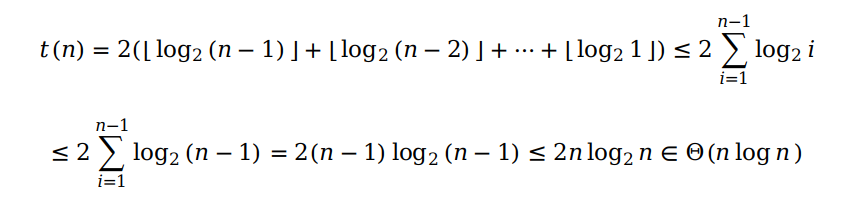
最后计算出堆的删除操作在最坏的情况下不会高于 Θ(nlog n) 的复杂度。
所以我们可以得到堆排序的复杂度,即两者相加后的复杂度: Θ(n) + Θ(nlog n) = Θ(nlog n)。
堆排序在任何情况下复杂度都保持在 Θ(nlog n),不需要额外的存储空间,但堆排序是一个不稳定的排序。在计算的时候我们发现堆排序的比较次数前面有一个常数 2,所以在通常情况下会稍逊色于快速排序和归并排序。如果你分别运行 GitHub 里我写的这三种排序的代码,你会发现堆排序的平均比较次数会高于快速排序和归并排序,消耗的时间也比这两者要多,下面给出了在我的电脑上运行的结果。
>>> python "heap sort.py"
>>> 平均比较次数:235346
平均运行时间:0.0616 s
>>> python "merge sort.py"
>>> 平均比较次数:120467
平均运行时间:0.0569 s
>>> python "quick sort.py"
>>> 平均比较次数:156098
平均运行时间:0.0348 s
→ 本节全部代码 ←