Lomuto 划分
前面我们学习了分治的思想:将一个大问题划分为若干个小问题,然后逐个解决小问题,最后将小问题的解合并成大问题的解。这一节的内容,我们会继续用分治来解决排序问题,但这一次我们更强调“分”。
在对一个无序的数组进行排序的过程中,我们总是期望将小的元素放在数组的左侧,而将大的元素放在数组的右侧。Lomuto 划分就是一种将数组划分成两部分的算法,首先,我们需要选一个中间值来作为我们的中轴(pivot),所有比中轴值小的元素位于中轴的左侧,而大于等于中轴值的元素位于中轴的右侧。
那么具体该怎样来实现这个过程呢?以下面的数组为例,首先,我们需要选择一个值当做中轴,这里我们选择数组的第一个元素。
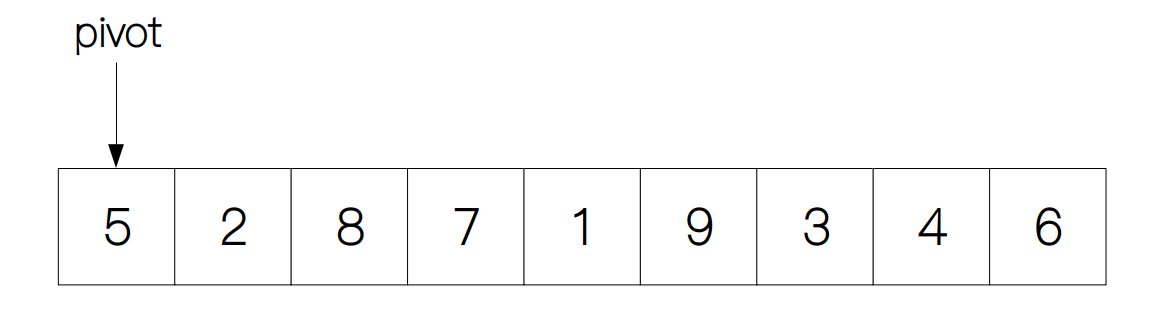
选好中轴之后,我们需要把中轴放到相应的位置,使得中轴左边的元素小于中轴值,中轴右边的元素大于或等于中轴值。这里我们要用到两个变量i和s,其中i指向第二个元素并开始递增。在每次循环中,如果array[i]的值小于中轴,s则向右移动一个单位,然后交换array[s]和array[i]的值,使得比中轴小的值总是位于数组的左侧。最后,我们交换pivot和array[s]的值,这样中轴就被放到了正确的位置了。

代码实现:
def partition(a):
l = 0; r = len(array) - 1
pivot = a[l]
s = l
for i in range(l+1, r+1):
if a[i] < p:
s += 1
a[s], a[i] = a[i], a[s] # 交换 a[s] 和 a[i] 的值
a[l], a[s] = a[s], a[l] # 交换 a[l] 和 a[s] 的值
return s
由于代码中只有一个for循环,基本操作执行了 n - 1 次,所以 Lomuto 划分的时间复杂度为 Θ(n)。
快速排序
我们知道,执行一次 Lomuto 划分后数组分为了两部分。要想让整个数组有序,我们只需要使左半部分和右半部分分别有序即可。假设中轴插入的位置恰好在数组的正中间,我们就可以用一个关系式来表达快速排序中 Lomuto 划分的过程。
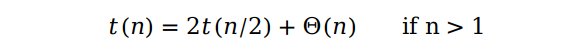
如果数组的长度小于等于 1 就直接return,也就是这里的递归出口。快速排序其实就是递归地执行划分数组的一个过程。
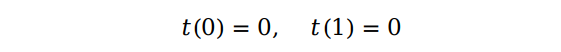
因此,我们就可以写出快速排序的 Python 代码:
def quick_sort(array):
# 数组长度至少大于 1
if len(array) > 1:
s = partition(array)
array[0: s] = quick_sort(array[0: s]) # 左半部分
array[s+1: len(array)] = quick_sort(array[s+1: len(array)]) # 右半部分
return array
最后,让我们用一个动画(来源于网络)来直观地感受一下吧!
复杂度分析
下面来分析一下快速排序的复杂度。前面已经提到过,如果中轴恰好将一个数组对等地分为了两部分,再根据递归关系式:t(n) = 2t(n/2) + n - 1。我们就可以推出,在最好情况下,快速排序的复杂度为 Θ(nlog n)。
如果数组正好是升序排列的,因为每个元素都小于等于它右侧的元素,所以在每次划分中,中轴并没有将数组对半分,而是将长度为 n 的数组分成了长度为 1 和长度 n - 1 的数组。因此,递归关系式就变为了:t(n) = t(n-1) + n - 1,最后推导出在最坏的情况下其时间复杂度为 Θ(n2)。
让我们再用一个动画(来源于网络)来感受一下在最坏的情况下的快速排序。
从动画中可以看出,我们对中轴的选择尤为重要,除了简单粗暴地选择数组的第一个元素之外,我们还可以从数组中随机挑选一个元素,也可以选第一个元素,中间元素和最后一个元素中的中位数来最为中轴,来尽可能地保证每次递归后中轴恰好能够对等分数组,用以达到分治的效果。
我在这节的代码中还模拟了平均情况和最坏情况下比较次数和运行时间,最后的结果如下:
平均情况:
平均比较次数: 157748
平均运行时间:0.0347 s
最坏情况:
平均比较次数: 49995000
平均运行时间:6.5079 s
稳定性
最后来看看快速排序的稳定性,我们看到,每次在pivot和array[s]交换顺序的过程中元素都有较大的跨度,因此我们猜测可能是不稳定的排序。要验证这个猜想,我们只需要举出一个特例即可。

一轮递归后,两个 4 的相对位置发生了变化,所以我们得出,快速排序是一个不稳定的排序算法。
→ 本节全部代码 ←