分治
分治(divide and conquer)是算法的五大经典思想之一。我们知道减治是通过缩小问题规模来解决问题,而分治法是先将一个大问题分成若干个小问题,然后逐一解决小问题,最后将小问题的解合并成原来大问题的解。听起来一定很抽象吧,没关系,下面的一个例子你马上就能明白。
小的时候我们一定都玩过类似乐高的玩具,当你花了几天的时间拼出一件作品时,你一定是满满的成就感吧。其实,我们在整个拼接的过程中就用到了分治的思想。以拼一栋房子为例,我们肯定不会一个零件一个零件地拼,而是先将这些零件组合成一个一个的小部件(例如屋顶,窗户等),然后把这些小部件拼接起来,组成更大的部件,然后这些大部件再相互拼接,最后拼出整栋房子。

假设整个作品由 n 个零件组成,它由 b 个规模相等的小部件拼接而成,一次需要拼接 a 次,每次拼接的时间为 f(n)。所以,根据这个关系,我们可以写出下面的关系式:
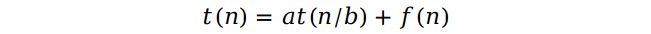
其中,f(n) 是关于 n 的一个函数,这里我们可以把它视作一次拼接所需要的时间复杂度,Θ(nd),d 代表复杂度的阶数。根据 a, b, d 不同的取值,我们可以借助 Master Theorem 来求得不同情况下的复杂度:
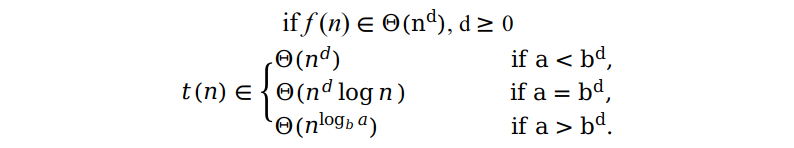
公式具体的证明过程在 Levitin 算法书的附录里,大家感兴趣可以去自己研究研究,后面的例子在计算复杂度的过程中会直接套用这里的公式。
有序数组的合并
我们可以将两个有序的数组合并成一个有序的数组看做是两个小部件的拼接过程,那具体要怎么来实现呢?让我们来举一个例子吧。
假设下面两个数组 a 和 b 要合并,我们需要一个空数组 c 来存放 a 和 b 中的元素。

具体步骤如下:
- 第一步:用三个变量 i, j, k 来分别记录数组 a,数组 b 和空数组 c 的索引值,并将它们都初始化为 0。

- 第二步:比较 a[i] 和 b[j] 的大小,将较小的元素存入到空数组 c 中。

- 第三步:较小元素的数组索引值和数组 c 的索引值分别加 1。

- 第四步:如果索引 i 和 j 都没有超出数组 a 和 b 的边界,执行第二步和第三步,否则执行第五步。

- 第五步:将含有剩余元素的数组全部存入到数组 c 中。

假设数组 a 和 b 分别有 n / 2 个元素,最好的情况要比较 n / 2 次,最坏的情况要比较 n - 1 次,所以合并有序数组的时间复杂度为 Θ(n)。
归并排序
归并排序的第一步操作就是递归地将数组等分,直到分割到只有一个元素为止,因为只有一个元素的数组一定是有序的,所以接下来我们再将这些元素两两归并,最后使整个数组有序。因此,归并排序可以像下面这张图那样描述:

代码由两个函数实现,一个是我们前面提到的合并有序数组的函数merge。
def merge(a, b):
i, j, k = 0, 0, 0 # 初始化变量
p, q = len(a), len(b)
c = [0 for i in range(p+q)] # 建立空数组
while i < p and j < q:
if a[i] <= b[j]:
c[k] = a[i]; i += 1
else:
c[k] = b[j]; j += 1
k += 1
while i < p:
c[k] = a[i]
i += 1; k += 1
while j < q:
c[k] = b[j]
j += 1; k += 1
return c
另一个是我们的主函数merge_sort。
def merge_sort(array):
if len(array) <= 1:
return array
m = len(array) // 2 # 中间位置
A = merge_sort(array[: m])
B = merge_sort(array[m:])
C = merge(A, B)
return C
复杂度和稳定性
最后来分析一下归并排序的复杂度和稳定性。前面我们知道归并的复杂度为 Θ(n),由于等分数组过程只执行一次基本操作,所以的等分的复杂度为 Θ(1),可以忽略不计。故我们可以得出下面的递归关系式:
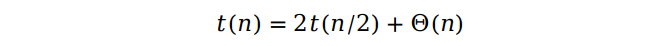
这个关系式的含义是,对长度为 n 的数组进行排序的时间复杂度等于对两个长度为 n / 2 的数组排序的时间复杂度,再加上分割和归并的时间复杂度 Θ(n)。根据前面的公式,我们可以得到归并排序的时间复杂度为 Θ(nlog n)。由于归并过程需要长度为 n 的空数组,所以归并排序的空间复杂度为 Θ(n)。
下面来分析一下稳定性,假设我们有数组 [4, 4, 2, 6], 按照上面的过程排序过后,我们发现相同的元素之间的顺序并没有发生变化,所以我们可以判定归并排序是一个稳定的排序算法。

归并排序的时间复杂度已经超越了前面讲到的所有排序算法,但它需要牺牲存储空间来实现。后面要讲到的计数排序也体现了这种思想。
→ 本节全部代码 ←