一个场景
在大学里,每当到了期末的时候,你一定会头疼于选课给你带来的困扰。其中一项就是先修课的问题,每次你高高兴兴地选了自己心仪的选修课时,却发现自己不满足先修课的要求,只好默默地退掉。到底怎样安排我们的课才能保证不会有这种麻烦呢?这一次,我们就来讨论一下这个问题。

假设大学里开设了这些课程:高等数学,线性代数,概率论,数据结构,机器学习和计算机视觉。它们存在这样的先修关系:线性代数的先修课为高等数学;概率论的先修课是线性代数;机器学习的先修课为线性代数,概率论和数据结构;最后计算机视觉的先修课是机器学习。
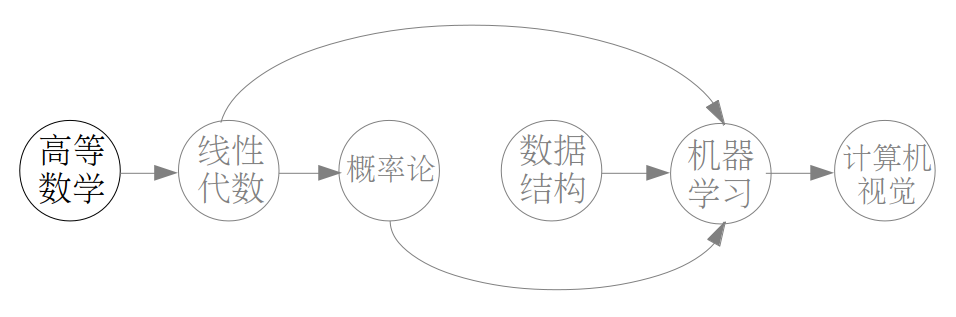
下面我们需要把这些课程和关系做一个抽象化的处理,说白了就是能够让计算机读懂这些关系。这里我们用图来表示这些关系,把每门课程当做图的节点,两门课的先修关系抽象为图的边,并且是带有方向的边,从一个节点 a 指向另一个节点 b 表示 a 是 b 的先修课。要是我们把这些关系用图表示出来就是下面这样:

这里,我们对上图进行类似“排序”的操作,也就是怎样安排这些课程使得一些课程不会因为先修课的原因而没有被选上,我们把这种操作叫做拓扑排序(topological sorting)。
卡恩算法
下面我们来分析一下这个问题,它跟我们前面提到的减治有什么关系呢?假如我们要在某一个学期修计算机视觉这门课,我们首先要保证修了机器学习这门课,而要达到修机器学习这门课的条件,我们又要修三门前置课,这样问题的规模在逐渐减小,直到这门课没有任何先修条件,我们就可以直接修这门课。
卡恩算法为我们提供了具体的步骤。
- 步骤 1:在图中找到没有被其它节点所指向的节点,即入度(在图论中,入度指的是所有进入该节点的节点个数)为 0 的节点。
- 步骤 2:删除该节点以及对应的边。

- 步骤 3:重复步骤 1 和步骤 2,直到图中没有节点为止。

最后我们用代码来实现一下:
首先还是构建节点 Vertex 类:
class Vertex(object):
def __init__(self, subject):
self.subject = subject
然后写出寻找入度为 0 的节点的函数:
def find_source(G):
source = None
V = G.keys(); E = G.values()
for v in V:
for neighbour in E:
for vertex in neighbour:
# 检查每条边
if vertex is v:
break
else:
continue
break
else:
source = v
break
return source
最后写出我们的主函数,我们用pop方法从图G中每次 pop 出入度为 0 的节点,但如果发现没有入度为 0 的节点,就说明这样的拓扑排序不存在,因此我们就提前终止程序。
def topo_main(G):
order = []
while len(G) != 0:
s = find_source(G)
if s is None:
return "不存在拓扑排序."
order.append(s.subject)
G.pop(s)
return order
在主程序中,我们先构建一个图G,然后执行topo_main函数,最后得到排序后的结果:
>>> print(topo_main(G))
>>> 排序结果为 ["高等数学", "线性代数", "概率论", "数据结构", "机器学习", "计算机视觉"]
其实,除了卡恩算法之外,我们还可以用 DFS 的方法。由于它跟减治的关系不是很大,这里我们就不做讨论了,感兴趣的同学可以去网上搜一搜这方面的内容。
→ 本节全部代码 ←