查字典
当我们在从字典中查找 “algorithm” 这个单词的时候,我们肯定不会傻傻地像二分查找一样首先从中间开始。相反,我们会从首字母为 a 的地方开始查找,然后根据第二个字母在字母表中的位置,找到相应的位置再继续查找,这样重复这个过程,直到我们查找到这个单词。
接下来我们就来介绍一下类似于上述过程的插值查找。
插值查找
插值查找(interpolation search)实际上是二分查找的改良版。假设有这样一个数组 [0, 10, 20, 30, 40, 50, 60, 70, 80, 90],我们可以发现,每个相邻元素的差均为 10,满足均匀分布。如果要查找元素 70,我们首先可以计算数组中小于等于 70 的元素占所有元素的比例的期望值 p = (70 - 0) / (90 - 0) = 7 / 9,而数组的长度 n 我们知道等于 10,所以我们期望查找的索引值就为 ⌊n × p⌋ = 7,对应的元素为 70,恰好就是我们要找的元素。这样,原本用二分法需要查找 3 次的用插值查找只用查找 1 次,大大提高了查找的效率。
这里,我们用一个公式来表示每次查找的期望索引值:
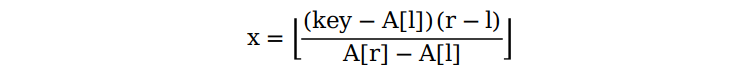
其中,l 和 r 分别代表数组的第一个和最后一个索引,key代表待查找的元素。
跟二分查找一样,如果一次查找失败,数组的长度就相应地减小,再代入上面的公式继续查找,直到查找成功或失败。
def formula(l, r, key, array):
p = (key - array[l]) / (array[r] - array[l])
n = r - l
idx = int(n * p)
return idx
def interpolation_search(array, key):
l = 0; r = len(array) - 1
while l <= r:
m = l + formula(l, r, key, array)
if array[m] == key:
return m
elif array[m] < key:
l = m + 1
else:
r = m - 1
return -1
复杂度分析
插值查找的平均复杂度为 Θ(log log n),但证明过程相当的复杂,这篇论文给出了详细的证明过程,感兴趣的同学可以自己去看看,这里我们就不再讨论了。
要是数组不是均匀分布的,插值查找的复杂度会退化到线性的复杂度 Θ(n)。举一个极端的例子,假设数组为 [0, 99, 100, 100, 100],我们要查找元素 99。第一轮查找我们计算出索引值为 3,第二轮为 2,第三轮为 1,这样我们查找了三次。推广到含有 n 个元素的数组就需要查找 n - 2 次,所以复杂度就为 Θ(n)。
因此,插值查找的高效性只针对均匀分布的数组,而对于分布不均匀的数组,插值查找便不再适用了。
→ 本节全部代码 ←