减治
在这一章里面,我们会讨论一种解决算法问题的新方案。减治(decrease and conquer),全称叫做减而治之,是通过逐步缩小问题规模的方式来解决一个问题。可能你还不是很明白,别急,我们先上一个例子:假设 9 枚金币中有一枚是假的(假币的重量会比真币轻),现在给你一个天平,你需要用最少的次数找出这枚假币。

你可以一枚一枚地称,但最多你可能要称 8 次才能称出来,不是非常高效。其实我们可以将这些金币对半分,也就是将 9 枚金币分为 4 枚和 5 枚。因为只有当天平两边的金币数要是相同的情况下我们才能判断哪边轻哪边重,所以这里需要从 5 枚里取出 1 枚。这样如果拿出的那一枚不是假币的话,经过一次称量后,我们只需要从较轻的 4 枚中找到假币,于是又可以对半分,称量之后,再从其中较轻的两枚中选择。这样以此类推,直到我们找出假币。
我们可以看到,原问题是从 9 枚金币中找出假币,经过一次称量之后,问题变为了从 4 枚金币中找出假币,再次称量后问题的规模变为了 2,最后变为 1,即找到假币。这就是减治法的思想:一个大问题被一次又一次地拆分成了更小的问题,直到我们能够直接解决小问题。
插入排序
小时候你一定玩过扑克牌,当你在整理那些乱序的牌的时候,你想到的第一种方法一定是将这些新摸到的牌插入到对应的位置,以此来达到手牌有序。

让我们以数组为例,假设有下面的数组:

我们可以看到,前面 3 个元素已经有序,后面 7 个元素还是无序状态,这时候我们需要将第 4 个元素插入到相应的位置,这样有序序列就从 3 增加到 4,无序序列就从 7 减小到 6。
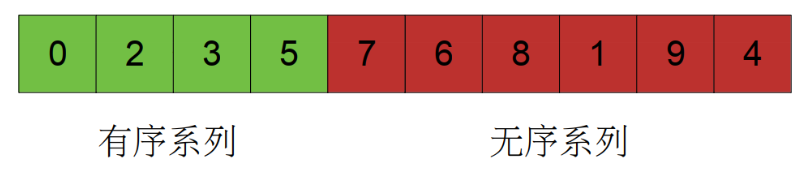
如果对于一个含有 n 个元素的完全无序的数组,我们可以把第一个元素视作有序,其余 n - 1 个元素视为无序,因为只有一个元素的数组肯定是有序的,所以每次将无序序列的第一个元素插入到相应位置后,问题的规模就减少 1。如果我们重复 n - 1 次,数组就从无序变为有序了。
最后我们用代码实现一下插入排序。
def insertion_sort(array):
for i in range(1, len(array)):
v = array[i]
j = i - 1
while j >= 0 and array[j] > v:
array[j+1] = array[j] # 用前一个元素覆盖当前元素
j = j - 1
cnt += 1
array[j+1] = v # 循环结束后,将 v 插入到相应位置
return array
复杂度分析
最好情况
插入排序的复杂度分析不同于之前讲到冒泡和选择排序,我们需要考虑不同实例下的数组。假设一个数组已经有序,在每次的 for 循环里,每个待插入的元素只需要跟自己前面的元素比较后就完成一次插入操作,即每个元素只比较一次。所以,对于一个含有 n 个元素的数组来讲,我们只需要比较 n - 1 次。
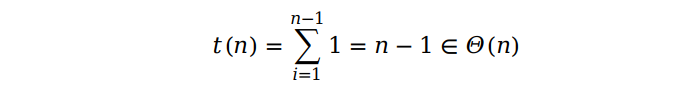
所以复杂度就为 Θ(n)。我们用一个动画(来源于网络)来直观地感受一下。
最坏情况
如果数组是倒序排列的,那么每次待插入的元素都要插入到第一个位置(假设数组元素不重复),也就是说,for 循环每执行一次,需要比较的次数就为 i 次,所以根据这个关系我们可以得出下面的式子:
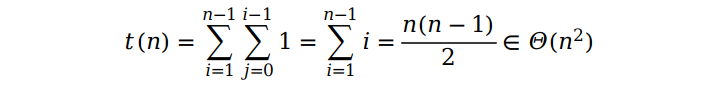
复杂度为 Θ(n2),从动画(来源于网络)时间的长短我们就可以看出,最坏的情况下算法的效率是比较低的。
平均情况
平均情况的复杂度分析相对来说就要稍微困难一点了,这里我们用基于概率的方式计算,对于第 i 个元素,它能够插入的位点有 i 处,每一处需要比较的次数分别为 1, 2, …, i。像下面这张图一样:
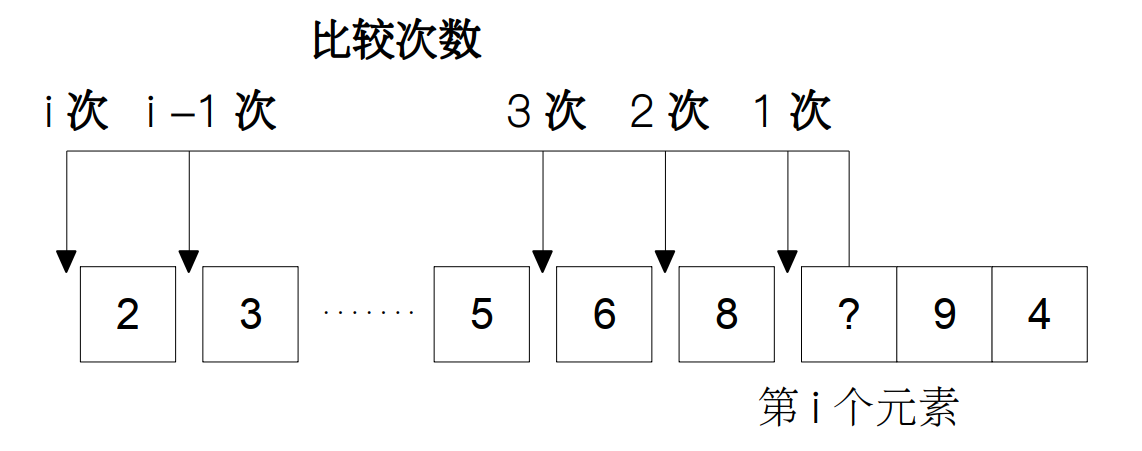
假设每个位点插入的概率相同,我们就可以得到下面的式子:
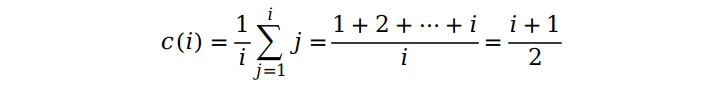
这说明了对于一个随机数组,第 i 个元素插入到相应位置所需要的平均比较次数为 (i+1)/2 次。对于整个数组而言,待插入的元素是从第 2 个开始,一直遍历到 n,所以只要把它们全部加起来,就能得到平均复杂度了。
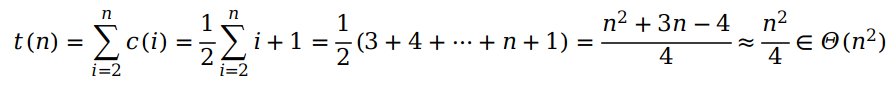
我们看到,虽然时间复杂度也为 Θ(n2),但是前面的系数变为了 1/4,说明插入排序在平均情况下的时间开销要低于最坏情况。为了证明这一结论,我在本节的代码里分别模拟了最好、最坏和平均情况所需要的比较次数和运行时间。下面给出部分结果:
最好情况:
平均比较次数: 9999
平均运行时间:0.0024 s
最坏情况:
平均比较次数: 49999962
平均运行时间:8.6132 s
平均情况:
平均比较次数: 24927061
平均运行时间:4.4334 s
最后来看看插入排序的稳定性,我们知道,将元素插入到正确位置后,只有那些比待插入元素大的元素会位于待插入元素的右侧,所以大小相同元素的顺序在排序后不会被打乱。因此,插入排序是稳定的排序算法。
从上面的结果来看,不论是比较次数还是运行时间,最好情况都要远远优于后面两种情况。所以如果数组是有序的或几乎有序的,采用插入排序会大大降低排序的时间,甚至比后面要讲到的排序算法还要快。
→ 本节全部代码 ←