有序表的查找
我们已经讨论过如何从数组中查找一个元素,采用的是最简单,最直接的顺序查找的方式,即从第一个元素开始,从左往右依次查找,直到查找到该元素或查找失败。我们知道顺序查找的在平均情况下的复杂度为 Θ(n),那么还有没有更快的算法呢?这一节我们就来讨论一下吧~
如果一个数组本身是有序的,查找一个元素就类似于在前面提到的猜数问题,只是这里要猜的数变成了查找的元素。如果我们从数组的中间位置开始查找,在每轮查找过后,我们只需要在剩下的长度为原来一半的数组中再继续查找,这样以此类推,直到查找到该元素,或查找失败。
来举一个具体的例子,假设我们有数组:

下面查找元素 61,经过一轮查找过后,待查找数组的长度变为原来的一半:

然后重复前面的过程,最终找到 61:

我们只需要十行左右的代码就能轻松实现二分查找:
def binary_search(array, key):
l = 0; r = len(array) - 1
while l <= r:
m = (l + r) // 2 # 向下取整
if key == array[m]:
return m
elif key < array[m]:
r = m - 1
else:
l = m + 1
return -1
最后来分析一下时间复杂度。我们从代码中看到,每次查找后,问题的规模都变为原来的一半,所以我们可以写出以下递归关系式。
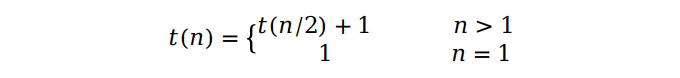
怎样来解这个关系式呢?这里我们不妨设 n = 2k,这样关系式就变为了 t(2k) = t(2k-1) + 1,然后再用回代的方式把它解出来。
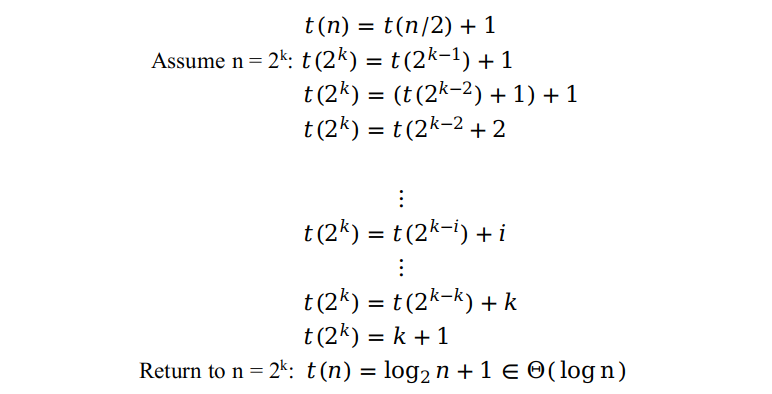
最后用 n 替换掉 k,得到复杂度为 Θ(log n)。
二叉搜索树
概念
如果像下面这幅图一样,把一个有序数组变成二叉树的结构,其中数组的中间元素作为树的根节点,左半部分的中间元素作为根节点的左孩子,右半部分的中间元素作为根节点的右孩子,第二层的节点以此类推,最后树的层数就会越来越多,这样我们就构建好了一颗二叉树。
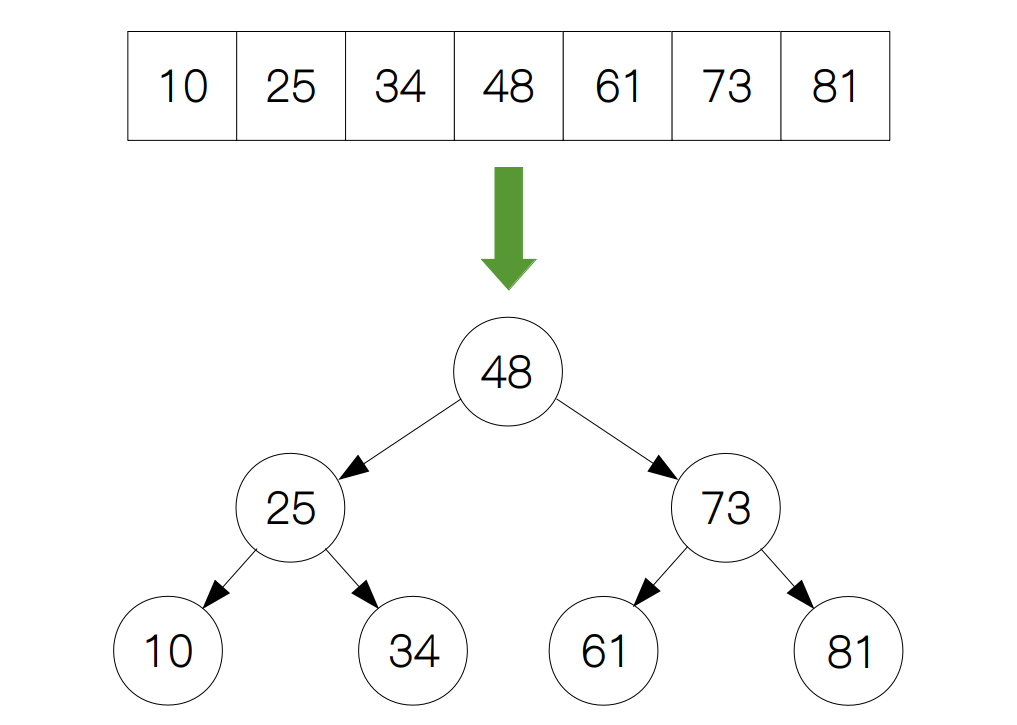
我们可以看到,对于每个节点而言,其左孩子都小于它的父节点,右孩子都大于等于它的父节点。所以我们把这样的二叉树叫做二叉搜索树(binary search tree)。
搜索
如果要搜索二叉树里面的元素(这里我们搜索节点 61),我们需要先从根节点开始访问。
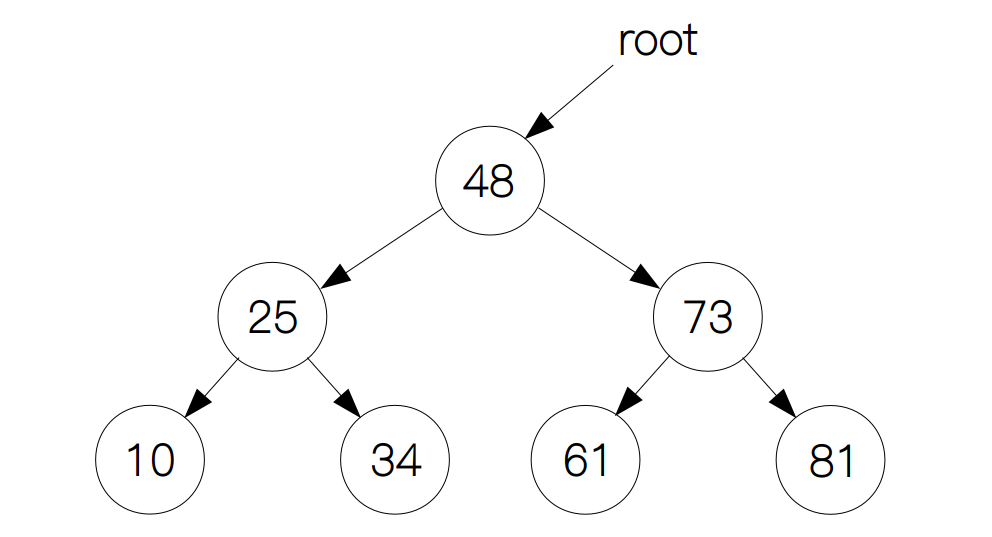
假如根节点的元素就是我们要找的,那么就直接返回该节点;如果搜索的元素比根节点大,我们就从它的右子树中继续搜索。在这个例子里,61 比 48 要大,所以我们从 48 的右子树中搜索 61,这样问题就变成了从以 73 为根节点的二叉树中搜索 61 这个元素。
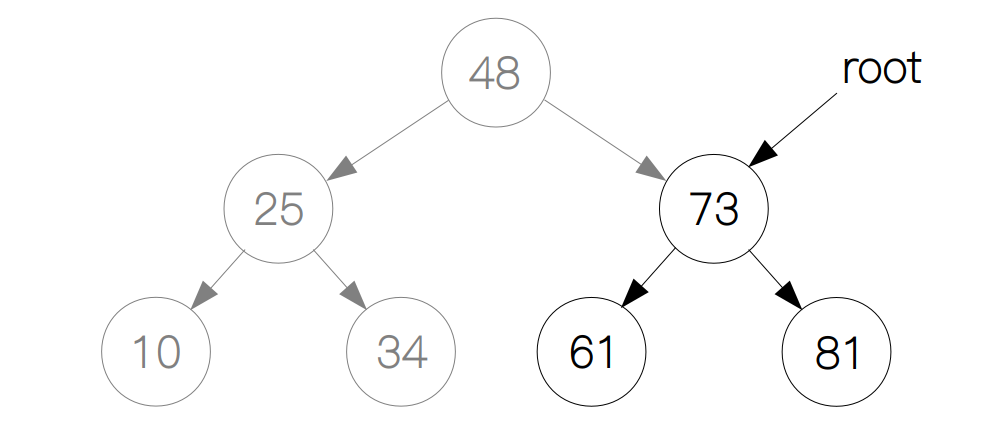
同理,如果搜索的元素比根节点小,我们就从它的左子树中继续搜索,这里 61 比 73 要小,所以问题又减小为了从以 61 为根节点的二叉树中查找 61 这个元素。
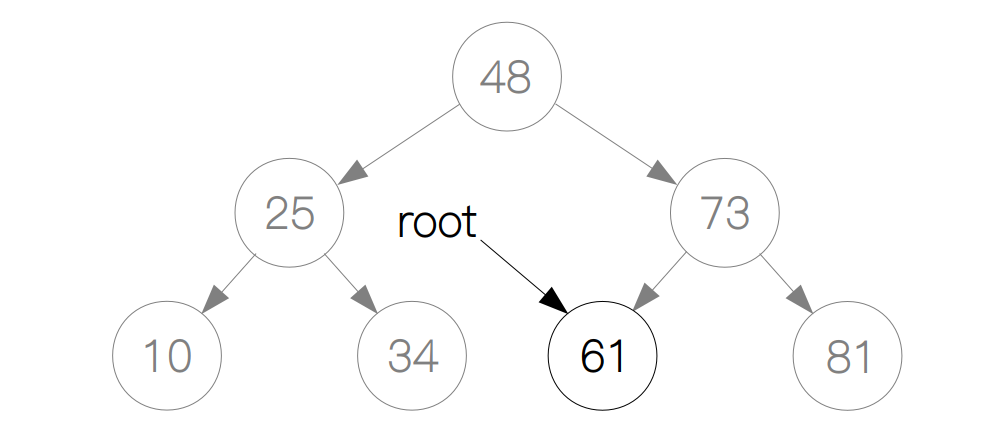
整个过程,我们用递归就能够轻松地实现。在此之前,我们先要构建节点Node 类和二叉树BST 类:
class Node(object):
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BST(object):
def __init__(self):
self.root = None
然后用两个函数来实现搜索的过程:
def search(self, value):
# 树的根节点为空就抛出异常
if not self.root:
raise ValueError("The tree is null")
return self.search_node(self.root, value)
def search_node(self, root, value):
if not root: # 如节点为空,则返回 None
return None
if value < root.value: # 从左子树查找
return self.search_node(root.left, value)
elif value > root.value: # 从右子树查找
return self.search_node(root.right, value)
else:
return root
插入
要想往二叉树里插入一个节点,我们首先要进行的步骤是先找到插入的位置,即通过前面的搜索操作找到插入位点。举一个例子,如果要插入节点 42,首先我们要先找到插入的位置(节点 34),因为 42 比 34 要大,所以 42 作为 34 的右孩子。
插入过程的代码实现:
def insert(self, value):
new_node = Node(value) # 创建一个新节点
# 查看根节点是否为空
if not self.root:
self.root = new_node
else:
self.insert_node(self.root, new_node)
def insert_node(self, root, node):
if node.value < root.value:
if root.left: # 从左子树查找
self.insert_node(root.left, node)
else:
root.left = node
else:
if root.right: # 从右子树查找
self.insert_node(root.right, node)
else:
root.right = node
删除
删除节点相对来说就要麻烦一些,除了要找到删除的节点以外,我们还要对不同情况的节点执行不同的操作。
情况 1:删除的节点为叶子节点
这种情况最简单,只需要找到该节点,然后删除即可,例如删除这里的节点 10。
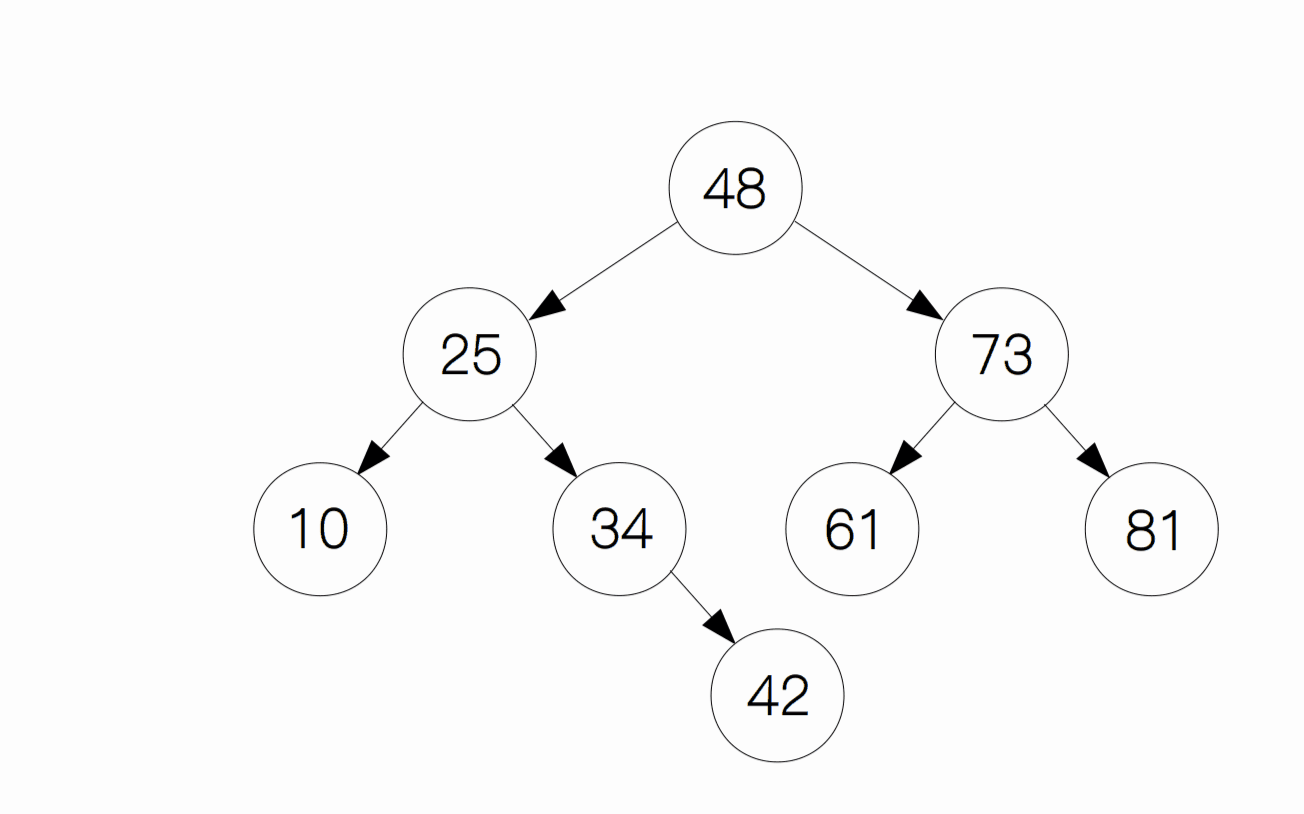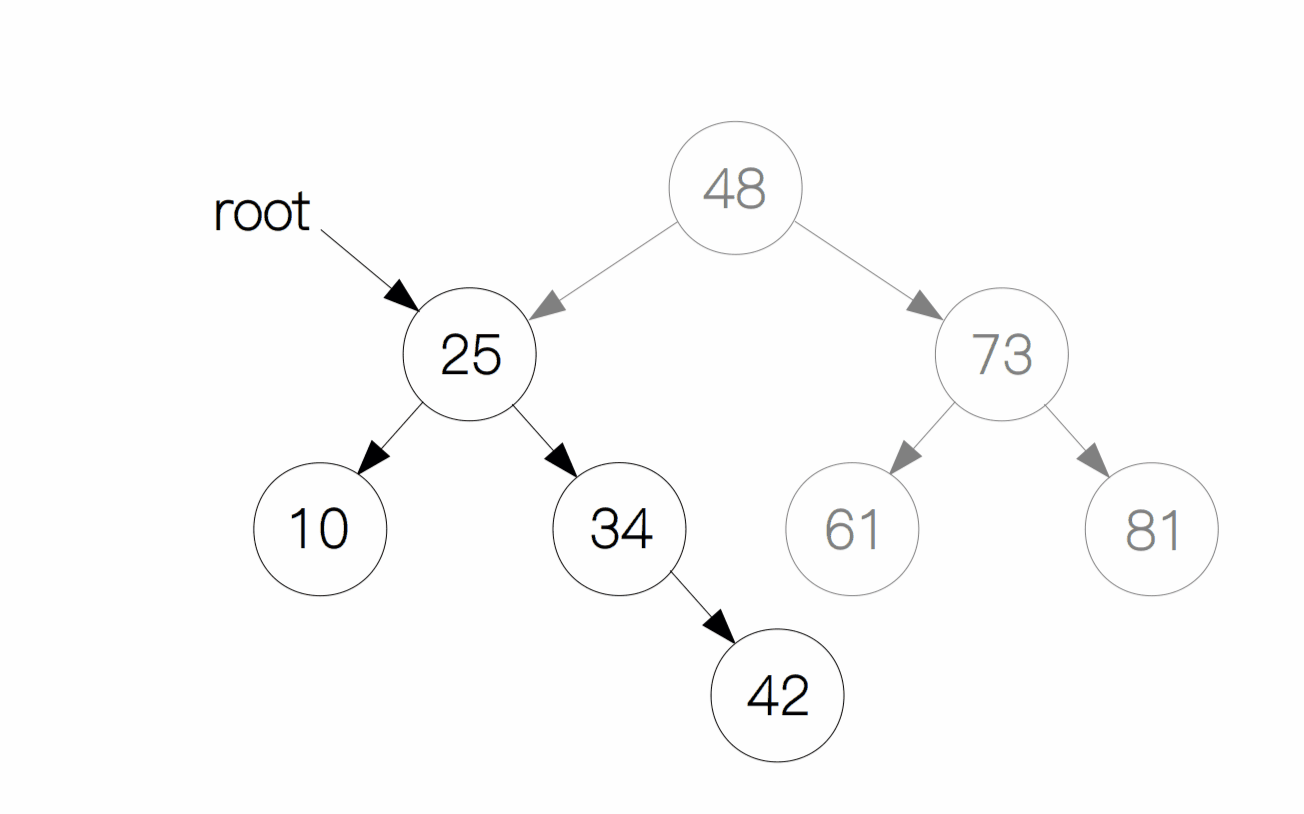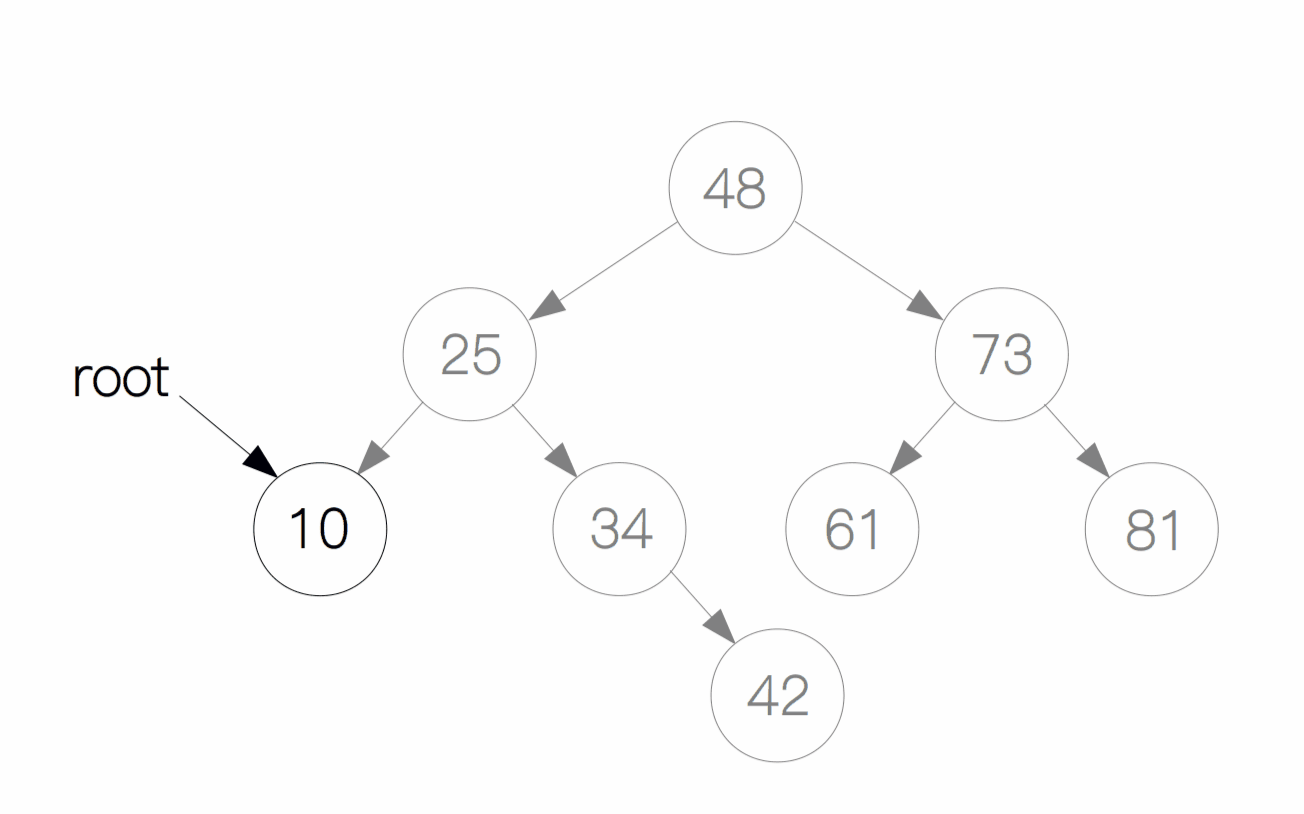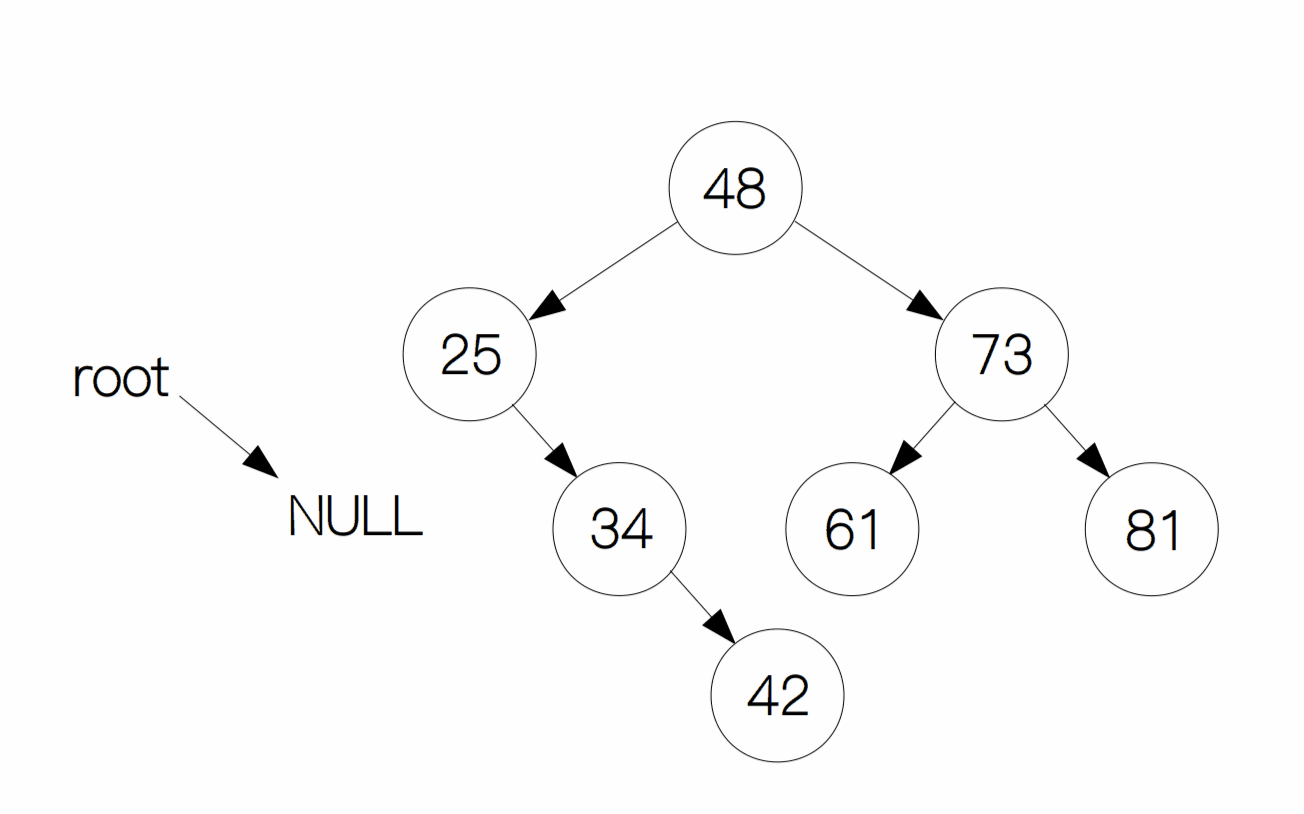
情况 2:删除的节点只有左孩子或只有右孩子
这种情况下,只需要将原本指向它的节点指向它的子节点即可。像下面这幅图一样,如果我们要删除 34 这个节点,只需要将节点 25 的右孩子指向 34 的右孩子(节点 42)即可,最后删除掉节点 34 。
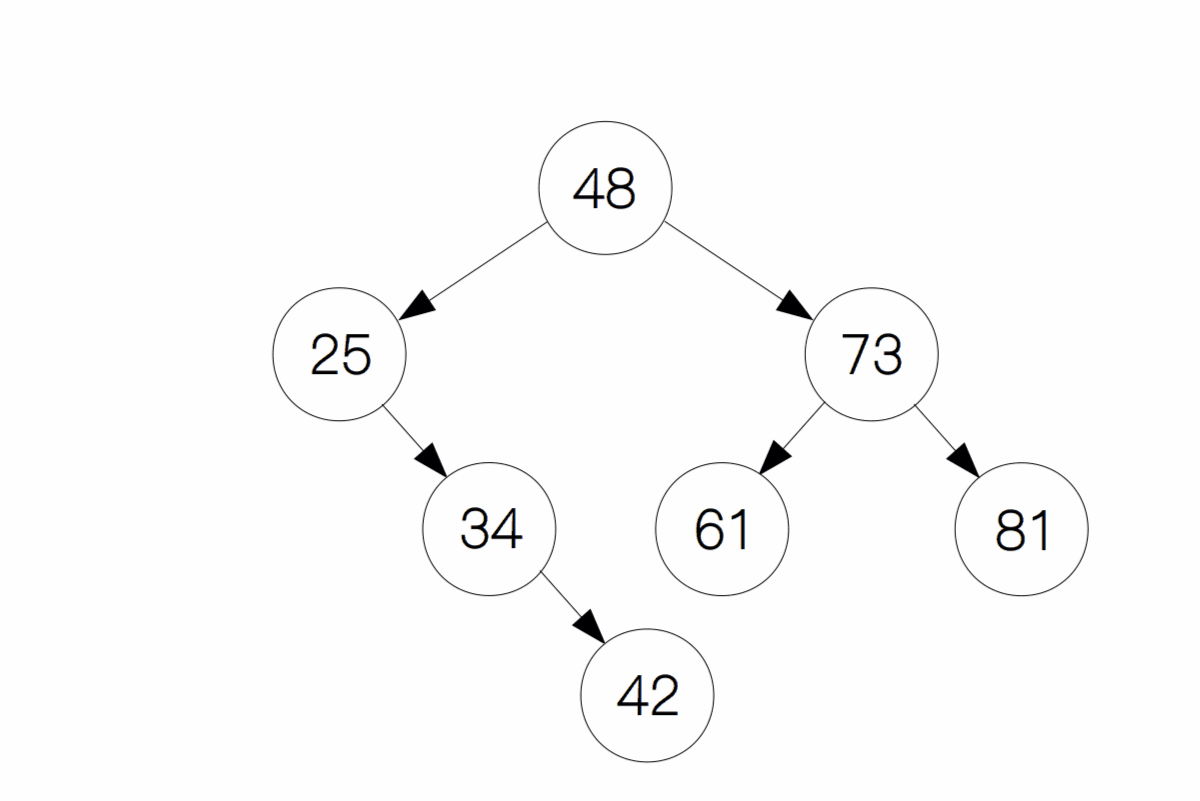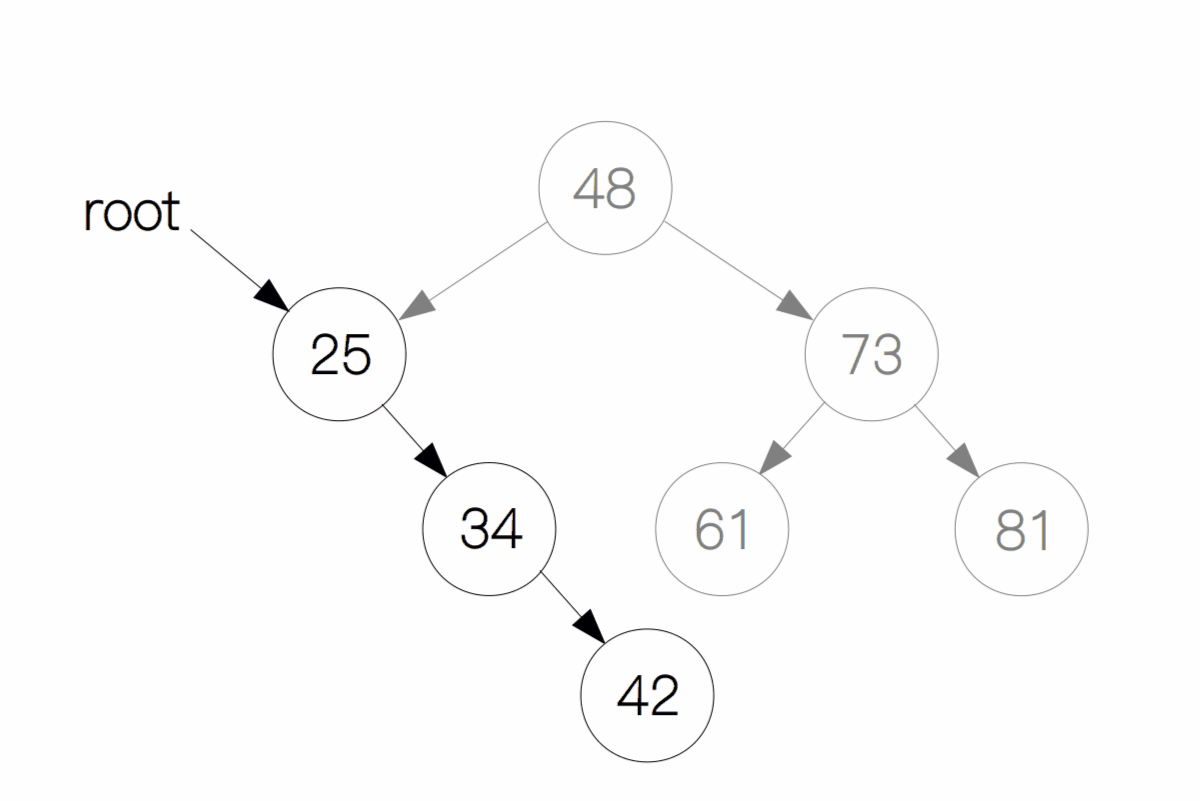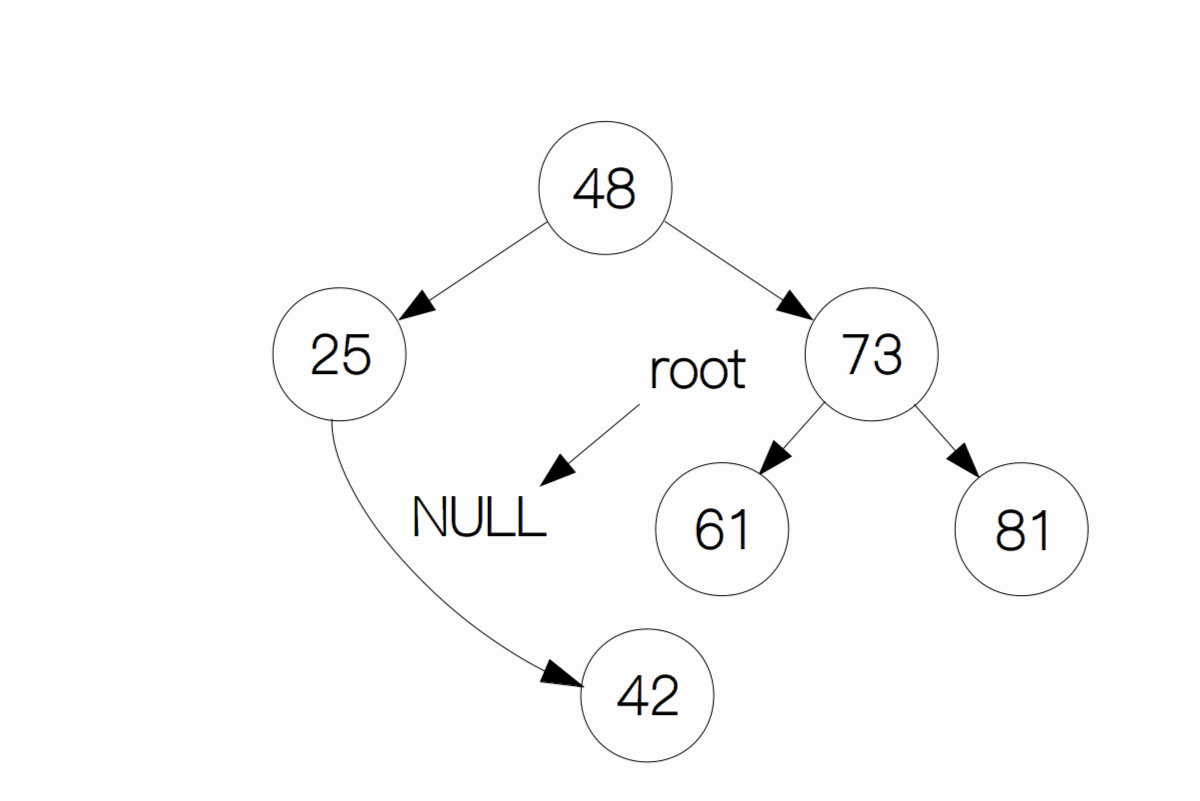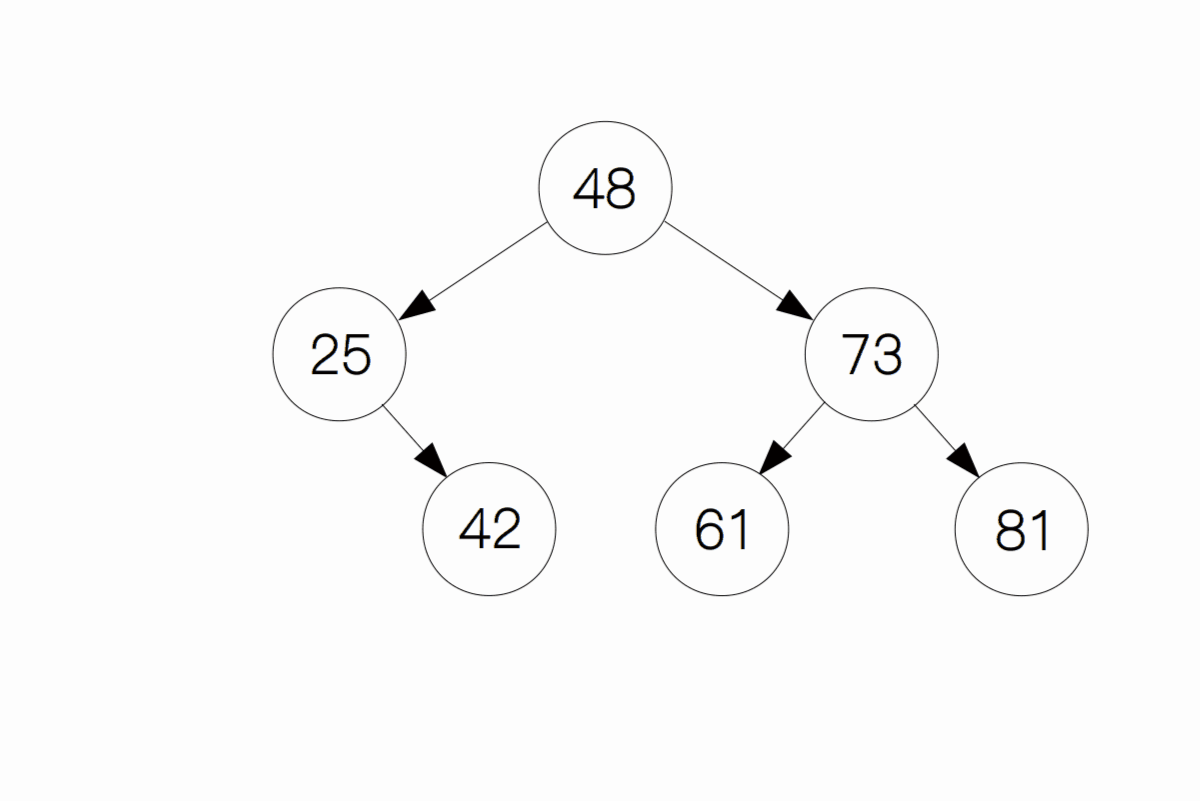
情况 3:删除的节点既有左孩子又有右孩子
这种情况是最麻烦的,删除节点后,要想保持原有二叉搜索树的性质,我们首先要从待删除节点的左子树中找到最大的节点(也叫前驱节点),或者从右子树中找到最小的节点(也叫后继节点)。这里以左子树为例,假设我们要删除节点 48,首先从它的左子树中找到前驱节点 42,然后交换它们的值,这样 42 就成为了根节点,原先的 42 变为了这里的 48,最后我们删除节点 48。
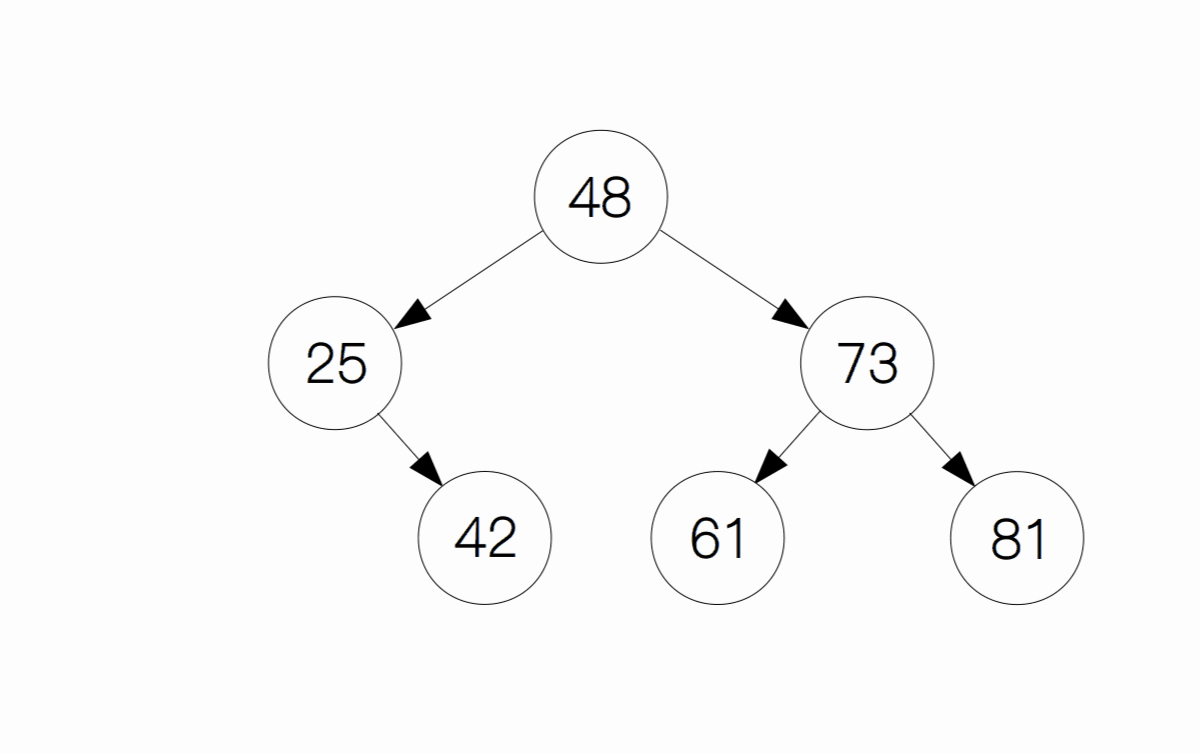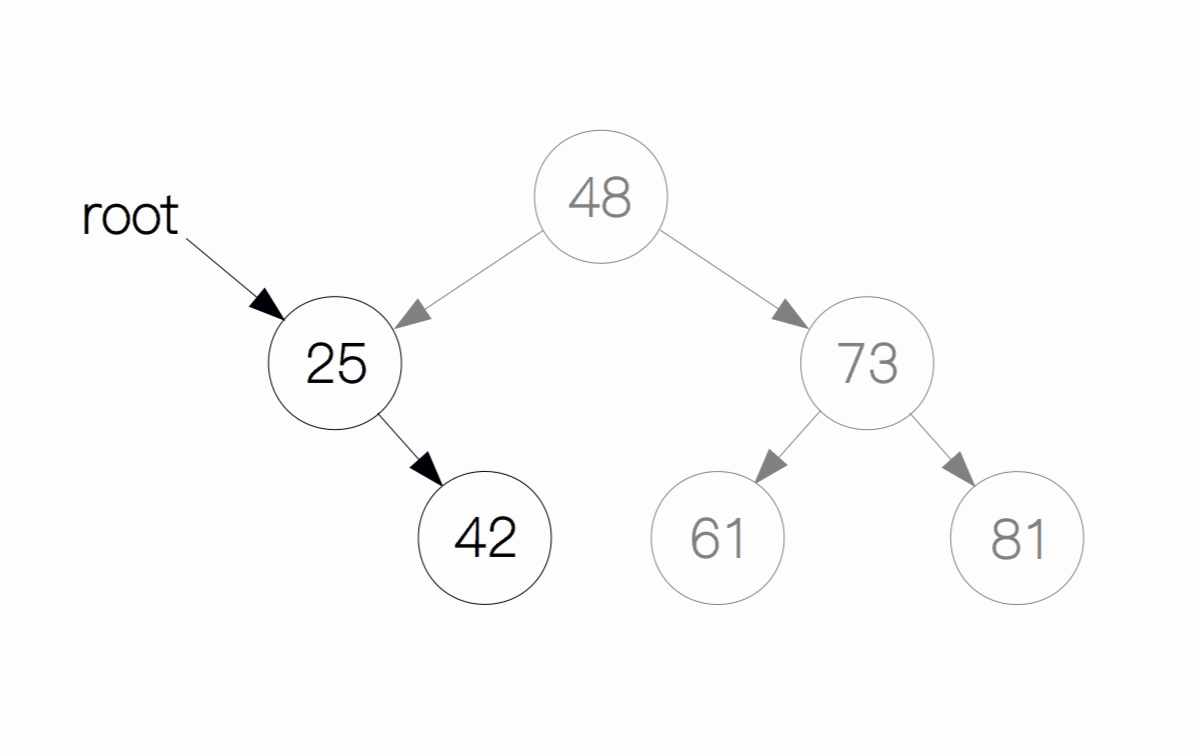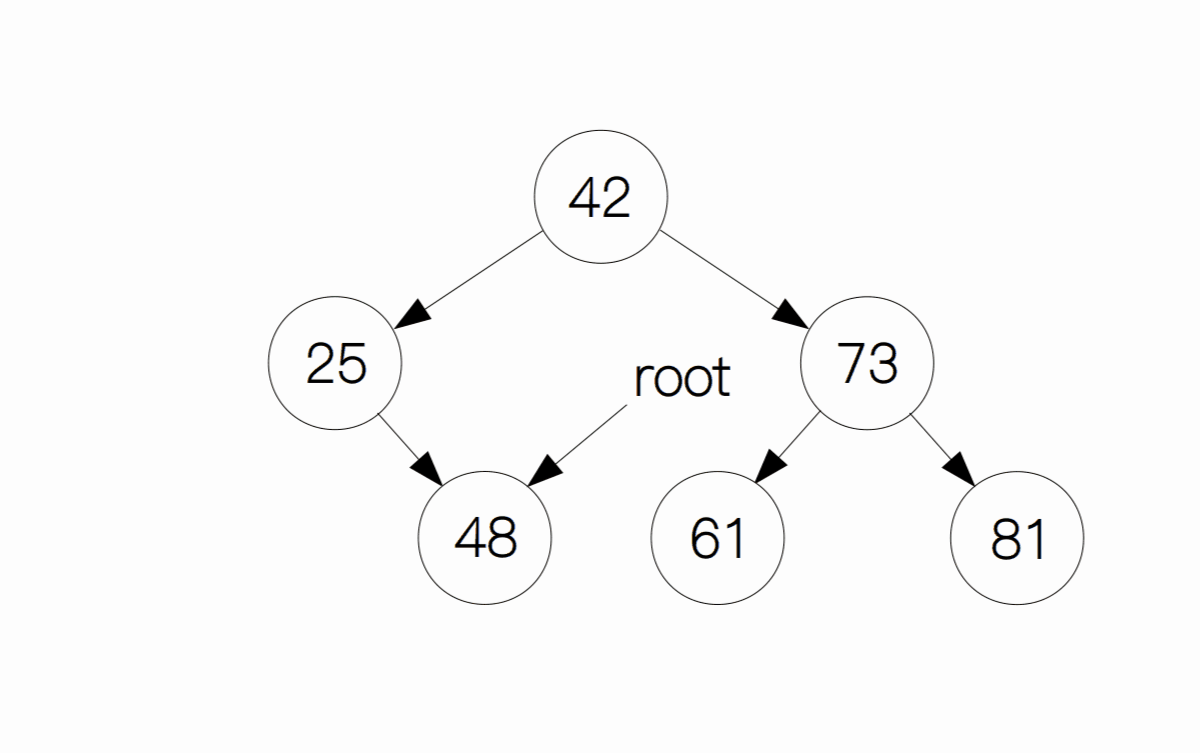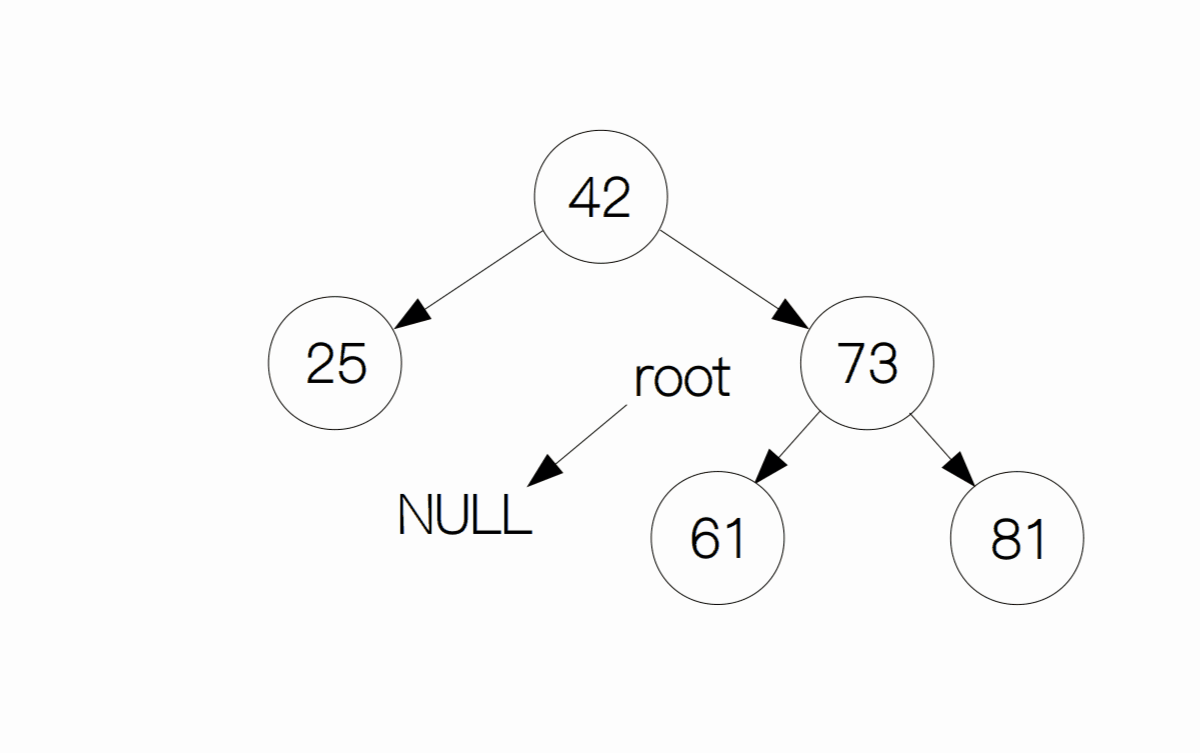
删除操作的代码实现:
寻找前驱节点的函数
def get_max(self, root):
if root.right:
return self.get_max(root.right)
return root
删除操作的两个函数:
def remove(self, value):
# 根节点为空抛出异常
if not self.root:
raise ValueError("The tree is null")
self.root = self.remove_node(self.root, value)
def remove_node(self, root, value):
if not root:
return None
# 查找
if value < root.value:
root.left = self.remove_node(root.left, value)
elif value > root.value:
root.right = self.remove_node(root.right, value)
else:
# 左右孩子为空
if not root.left and not root.right:
del root
return None
# 只有左孩子或右孩子
elif not root.left:
temp = root.right
del root
return temp
elif not root.right:
temp = root.left
del root
return temp
# 左右孩子都有
else:
temp = self.get_max(root.left) # 找到待删除节点的左子树的最大节点
root.value = temp.value
root.left = self.remove_node(root.left, temp.value)
return root
复杂度分析
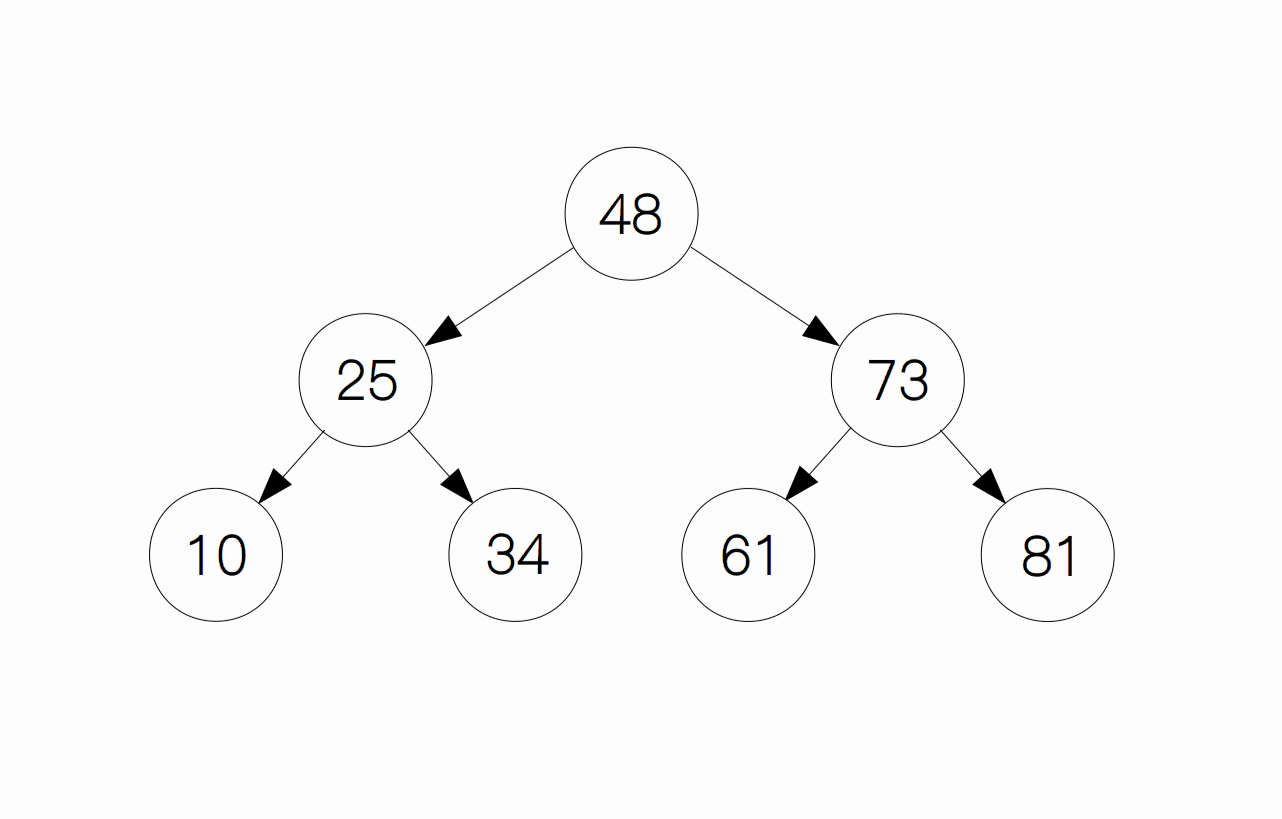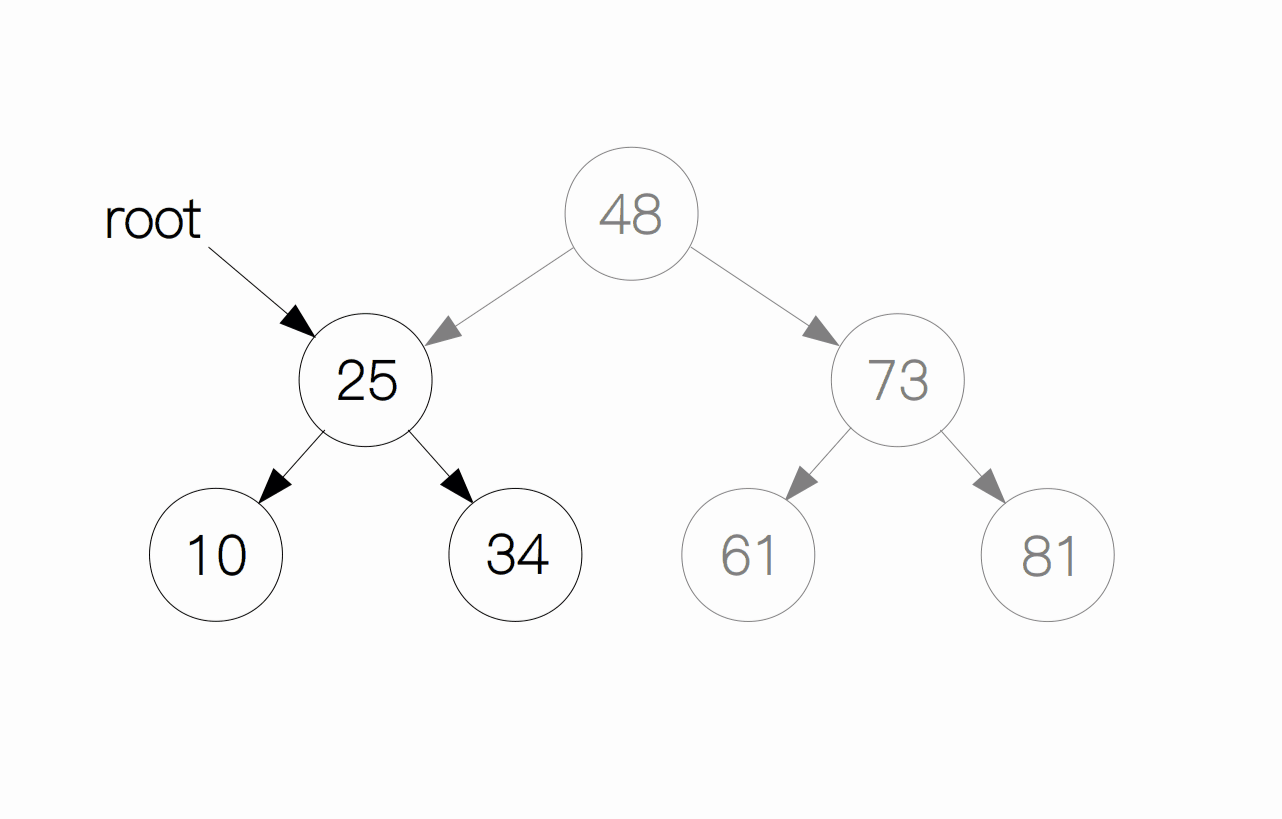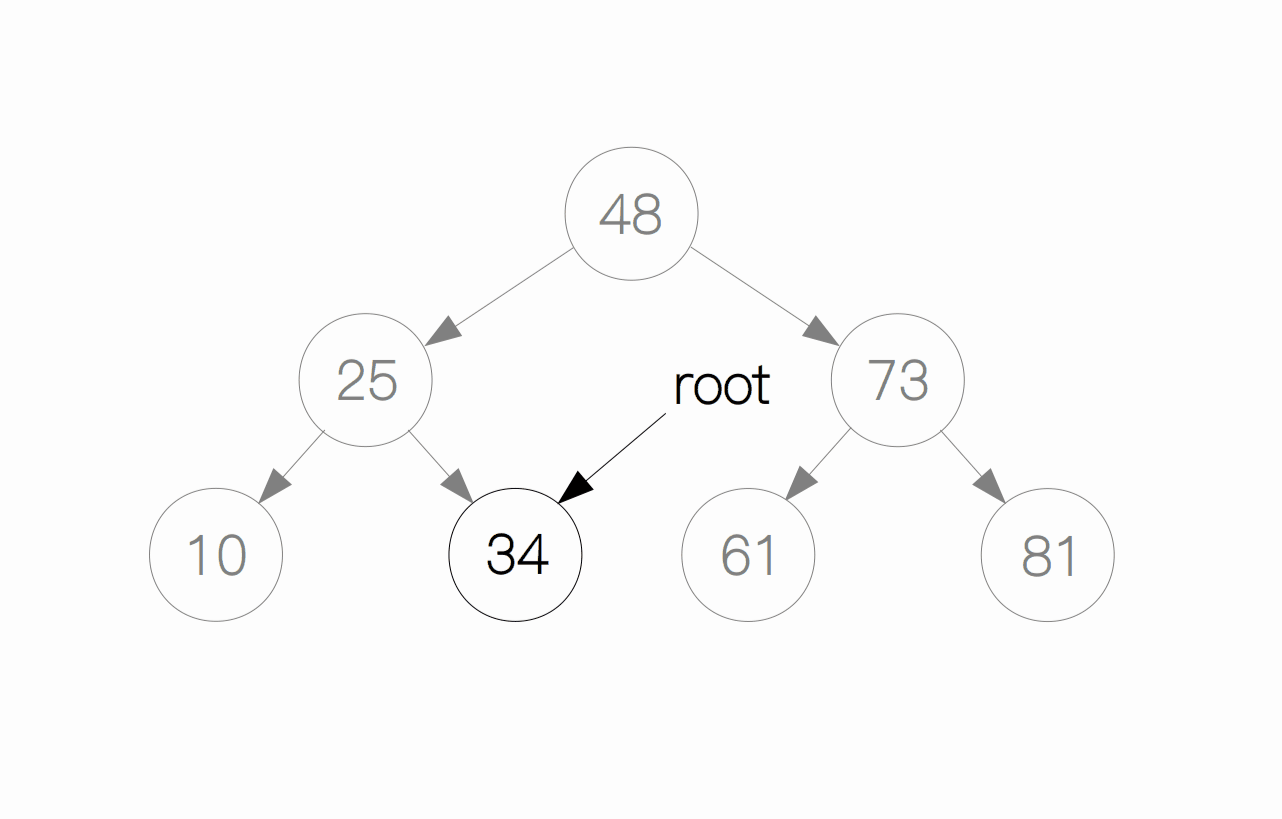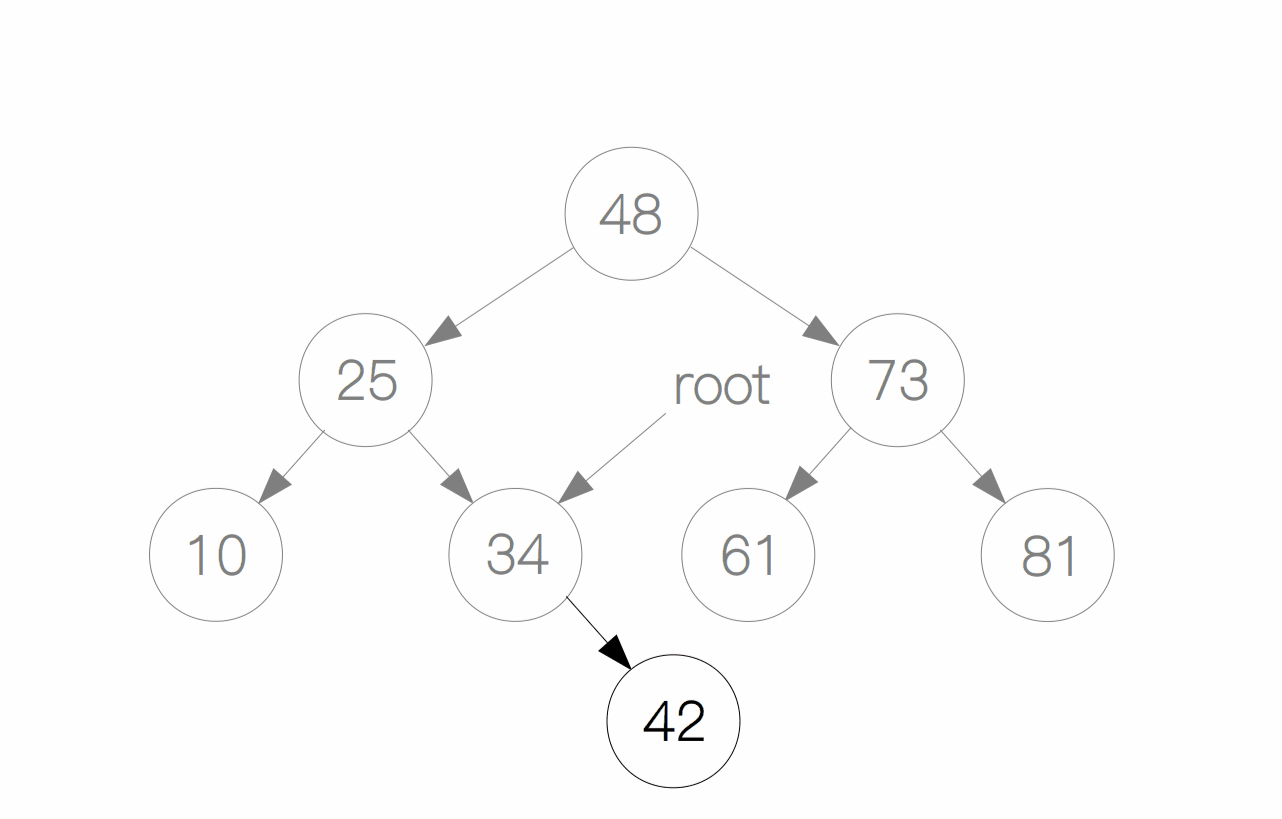
二叉搜索树的复杂度取决于二叉树的结构。如果像上面的例子那样,二叉树每一层都是满的,那么复杂度就跟二分查找一样,为 Θ(log n)。假设二叉树长得像下图的右边的树一样,我们会发现它显得特别地不平衡,跟普通的链表没有什么区别,所以在这种情况下复杂度就退化为线性的复杂度 Θ(n)。
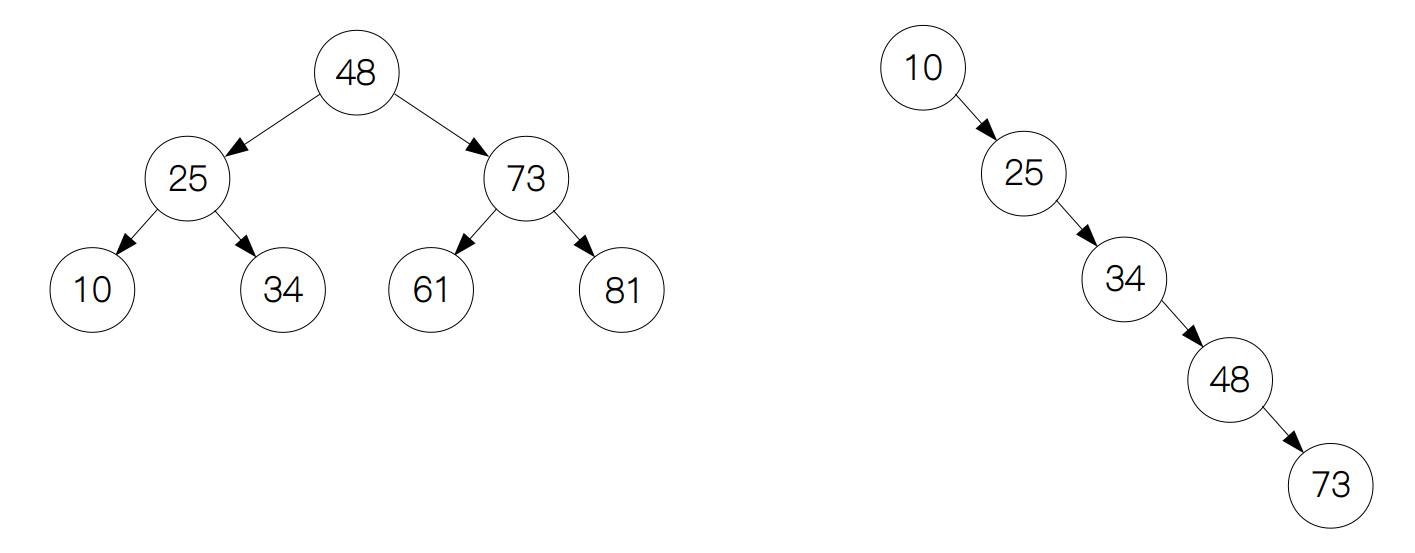
因此,二叉树的平衡性就显得尤为重要,后面我们要讨论的AVL树和红黑树会有自己独特的机制使不平衡的二叉树保持平衡。
→ 本节全部代码 ←