引入
前面我们讲到了求最大公约数的算法：欧几里得算法。我们先举一个具体的实例：24 和 16 的公约数。根据其公式gcd(m, n) = gcd(n, m mod n)，我们可以得到：gcd(24, 16) = gcd(16, 8) = gcd(8, 0)，所以最大公约数是 8。其实，除了用欧几里得算法以外，我们还可以采用更简单直接的方式，从 16 开始依次递减，如果存在两数都能够被整除，那么这个数就是最大公约数。写成代码的形式就是：
def gcd(m, n):
r = min(m, n) # 选较小者
while r != 0:
if m % r == 0 and n % r == 0:
return r
r -= 1
我们可以计算得出，该算法的if语句被执行了 9 次，而欧几里得算法只需要执行 3 次，我们可以看到两种方法在执行次数上出现了差异，换句话说就是算法的效率出现了不同。我们知道，当用一个算法解决问题的一个实例的时候，必然对应着算法运行的时间和所需空间（RAM）。一般来讲，当问题的规模 n 增大的时候，对应的运行时间 T 和所需空间 S 也会增大，于是时间复杂度（time complexity）的概念就是：当一个问题的规模 n 趋向于无穷大的时候，算法所需要的时间 T(n) 。当然，如果一个算法需要很大的内存空间，那么空间复杂度（space complexity）就是指当 n 趋向于无穷大的时候，算法所需要的空间 S(n) 。
用于约束的 O, Ω, Θ
那么问题来了，T(n) 的单位是什么呢？如果是秒的话，不同的 CPU，不同的操作系统，不同的运行环境，计算出的结果肯定是不一样的，所以我们很难定量地去描述这个问题，最后人们想到了用一个函数来约束 T(n)。其中大 O 符号约束了 T(n) 的上界（upper bound）。也就是说，当 n 在趋近无穷大的时候，T(n) 的大小总是小于等于某个函数。举个例子，前面用迭代法求最大公约数所耗费的时间跟问题的规模明显呈现的是一个线性关系，那么我们可以这样表示：T(n) ∈ O(g(n))，其中 g(n) = n。当然，T(n) 也满足 T(n) ∈ O(n2)。这里为了更好的理解，没有采用严格的数学定义，感兴趣的同学可以去维基百科一探究竟，这里我们就不细讲了。
同理，大 Ω 符号约束了 T(n) 的下界（lower bound），即 n 在趋近无穷大的时候，T(n) 总是大于等于某个函数。还是拿刚才的例子，T(n) 我们可以表示为 T(n) ∈ Ω(n)，代表其时间复杂度不会低于线性的复杂度，当然也不会低于常数的复杂度（不随 n 的变化而变化），所以也有：T(n) ∈ Ω(1)。
剩下的 Θ 符号就代表的是 T(n) 的确界（tight）了，就是说 n 在趋近无穷大的时候跟它时间复杂度一样的一个函数。所以前面的例子就有：T(n) ∈ Θ(n)。最后用三张图来直观地感受一下吧！
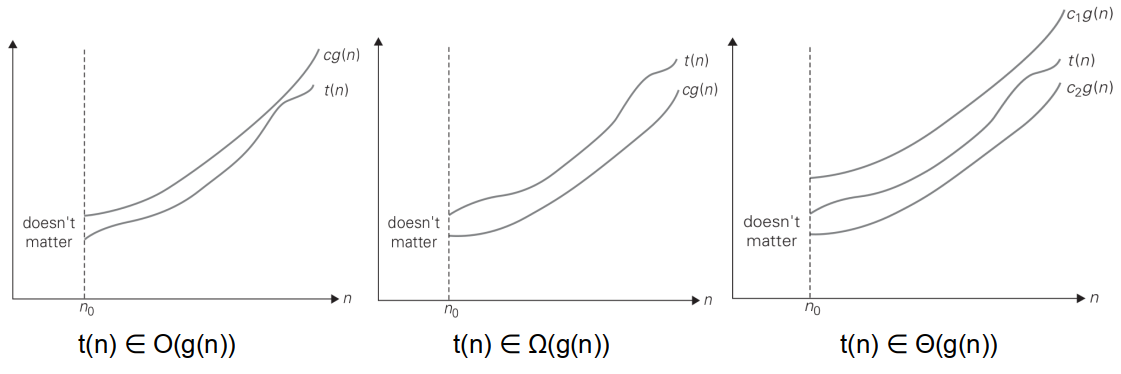
复杂度的比较
如果给定两个时间复杂度 O(f(n)) 和 O(g(n))，怎样来判断哪个时间复杂度比较大呢？根据复杂度的定义我们知道，一个函数在趋向于无穷大时的变化情况决定了复杂度的大小，而要比较两者的大小，我们可以通过做商的方式，像这样：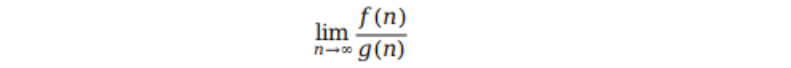
这个极限可能会出现好几种情况，让我们来分别讨论一下。
情况 1：极限为 0
假设 f(n) = n，g(n) = n2。那么我们就可以得出该极限为 0。
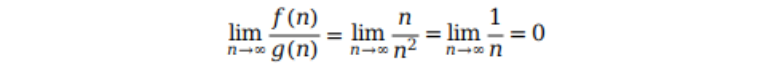这样我们可以认为当 n 趋近于无穷时，f(n) 的增长慢于 g(n) 的增长，即 f(n) 的复杂度低于 g(n) 的复杂度。情况 2 极限为 ∞
假设 f(n) = n，g(n) = log n。由于极限是无穷比无穷的未定式，所以我们可以借助洛必达法则，最后得出极限为 ∞
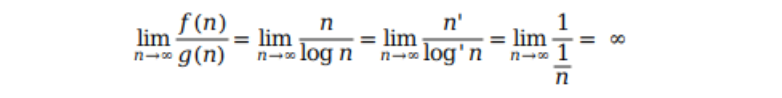这样我们可以认为当 n 趋近于无穷时，f(n) 的增长快于 g(n) 的增长，即 f(n) 的复杂度高于 g(n) 的复杂度。情况 3 极限为常数
假设 f(n) = 3n + 5，g(n) = 7n + log n。同样借助洛必达法则，最后得出极限为一常数 c
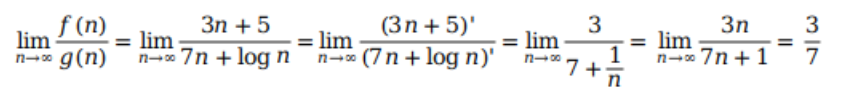这样我们可以认为当 n 趋近于无穷时，f(n) 的增长快慢和 g(n) 相同，即 f(n) 的复杂度和 g(n) 的复杂度相同。
从情况 3 我们可以观察出，两个函数的复杂度都由前面的部分决定（3n2 和 7n2），这间接地说明了前面的部分占据了主要的地位。因此，不同复杂度之间一定存在大小关系，也就是说随着 n 增大，T(n) 的增长存在快慢差异，于是我们可以把一些常见的复杂度排个序，并用一张图展示出来。
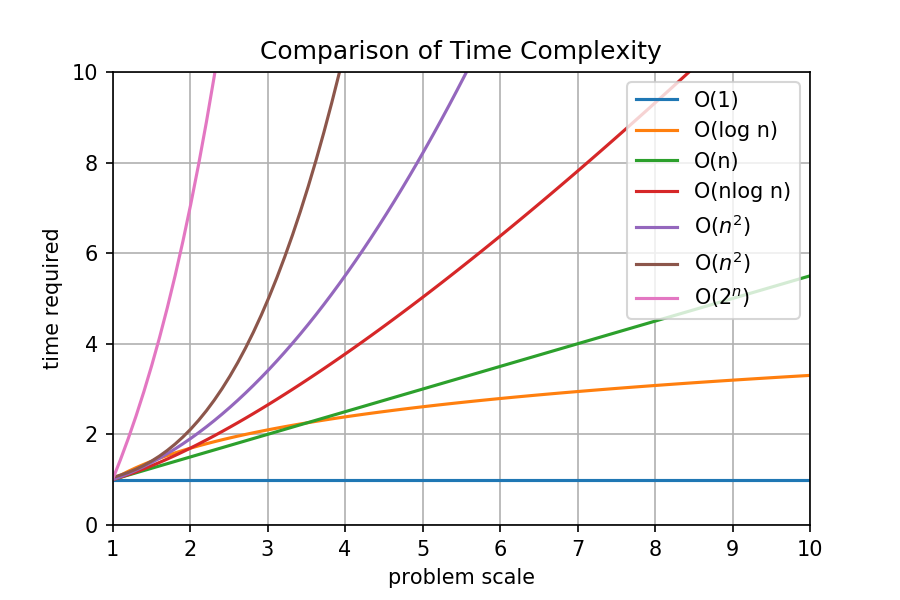
从左上到右下，其大小排列依次是：O(2n) > O(n3) > O(n2) > O(nlog n) > O(n) > O(log n) > O(1)。
