复杂度分析（递归）

什么是递归

前面我们对一些算法的复杂度进行了分析，但这些都是基于循环和迭代的，这一节我们会对递归的算法进行复杂度分析。首先要需要知道什么是递归，递归（recursion）是函数调用自身的一个过程。举个例子，假设你是一个英语水平有限的人，你在读一段英文材料中遇到了某个生词，你需要查字典去了解这个单词的意思，但是只给你了英英字典，意味着你要查找的单词下方的释义也有可能是你不认识的单词，于是你又继续去查找那些你不认识的单词，而那些单词的释义有可能又出现你不认识的单词，你又继续查找，如此往复，直到你能够全部看懂为止。这样一个过程我们可以把它看做是一个递归的过程，因为查字典这个动作在不停地调用自身。

字典

试想如果你的英语水平很糟糕，你可能查了很久的字典还是没有弄明白原来那个生词是什么意思，甚至出现单词 A 用到了单词 B 做释义，单词 B 又用到了单词 A 做释义这种情况，即出现死循环。那么递归结束的条件是什么呢？显然，如果一个单词的释义你全都能看懂，那就以为者当前递归就结束了，我们把这种条件叫做初始条件（initial condition），也叫递归出口。

阶乘的计算

阶乘大家应该都不陌生，一个数的阶乘 n ! = n × (n-1) × (n-2) × … × 2 × 1，所以我们自然而然想到的计算方法是从 1 到 n 把它们乘起来，但只要我们稍微观察一下便可以得到 n ! = n × ( n - 1) ! 这样的关系式。递归需要递归出口，因此这里我们规定 0 的阶乘等于 1，所以当 n = 0 时递归就停止了。用代码实现阶乘计算非常容易，只需要 4 行就可以搞定：

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n-1)

用一个数学递推式是来表达上面的关系：

关系式

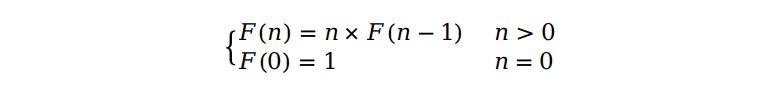
我们观察可以得到这样的规律：问题的规模由原来的 n 经过一次乘法运算 n × F(n - 1) 后变成了 n - 1，并且每经过一次乘法运算，问题的规模都会减少 1，所以要求计算阶乘的时间复杂度，我们可以推出如下的关系式：

关系式

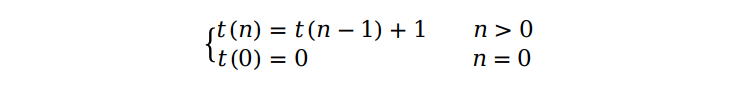
其中“+ 1”代表问题的规模每减少 1 就执行了一次乘法运算。我们把这样的关系式叫做递归关系式（recurrence relation），要解出这个关系式，我们需要一步一步地推导，具体来讲就是先将 n - 1 代入式子中得到一个新的递归关系式，再将它代入到原式子中就可以得到 t(n) = t(n - 2) + 2，一直重复这个过程，直到出现递归出口。

推导

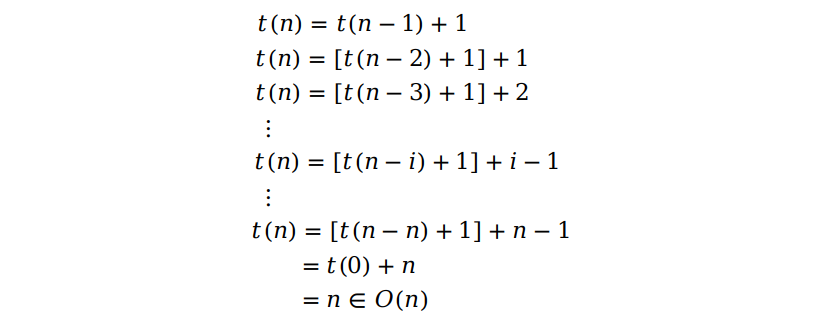
于是我们得出计算阶乘的时间复杂度为 Θ(n)。

汉诺塔

汉诺塔大家肯定都玩过，规则也很简单：有 A, B, C 三根柱子，上面穿有从大到小排列的圆盘，现在你需要借助 B 柱把 A 柱上的圆盘挪到 C 柱上，一次只能挪一个，且大的圆盘不能放在小的圆盘的上面。

演示

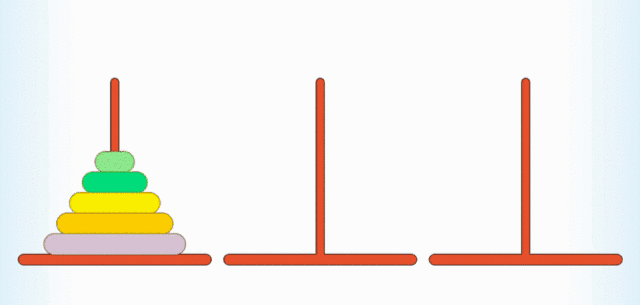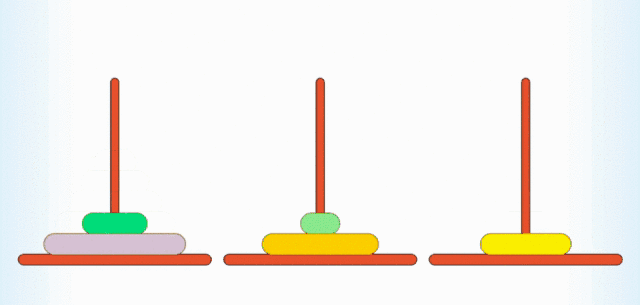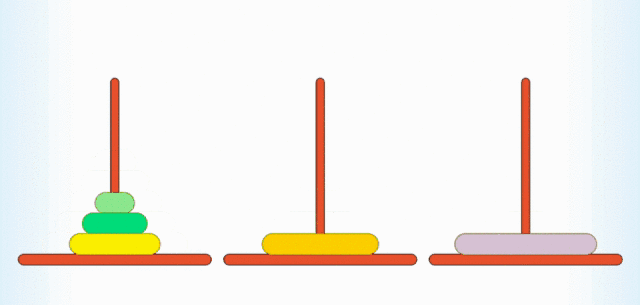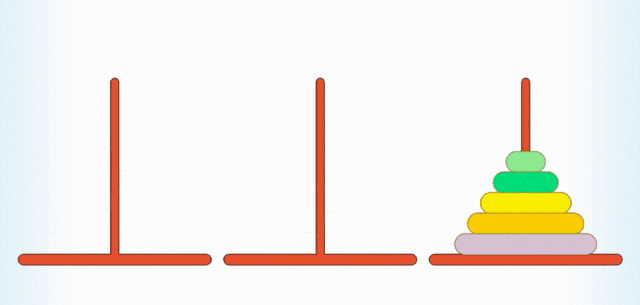
汉诺塔跟递归有什么关系呢？如果你是一个细心观察的人，你就会发现，要想把 n 个圆盘从 A 柱挪到 C 柱上，你首先要通过某种方法把 n - 1 个柱子从 A 挪到 B 柱上，给 A 柱上最大的圆盘“腾位置”，然后把最大的圆盘从 A 柱移动到 C 柱上，最后再通过某种方法把 B 柱上 n - 1 个圆盘挪到 C 柱上。至于怎么移动这 n - 1 个柱子，我们可以又用某种方法移动最上面的 n - 2 个柱子，给第二大的圆盘“腾位置”，再将 n - 2 个柱子移动到相应的柱子上。这样我们便可以一直递归下去，直到出现递归出口，也就是只有一个圆盘的情况。

我们用几张图来直观地理解一下，假设这里有 4 个圆盘，我们可以分为三个步骤：

状态0

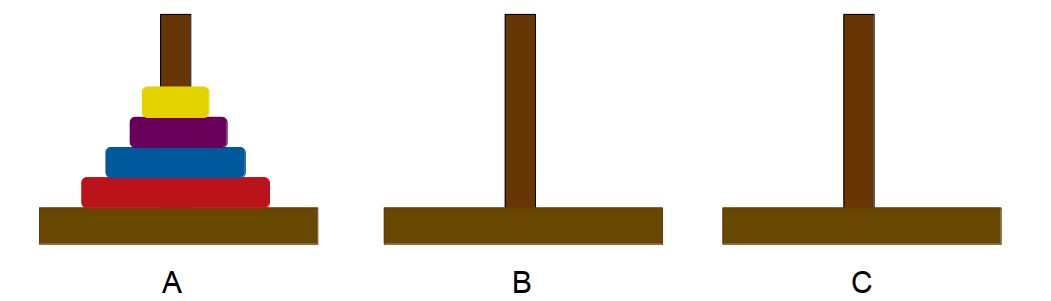
  • 步骤一：用某种方法将 3 个圆盘从 A 柱移动到 B 柱

状态1

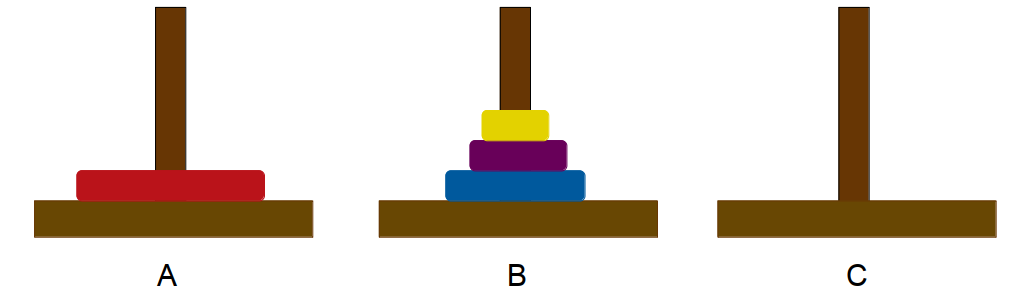
  • 步骤二：将 A 柱的圆盘移动到 C 柱

状态2

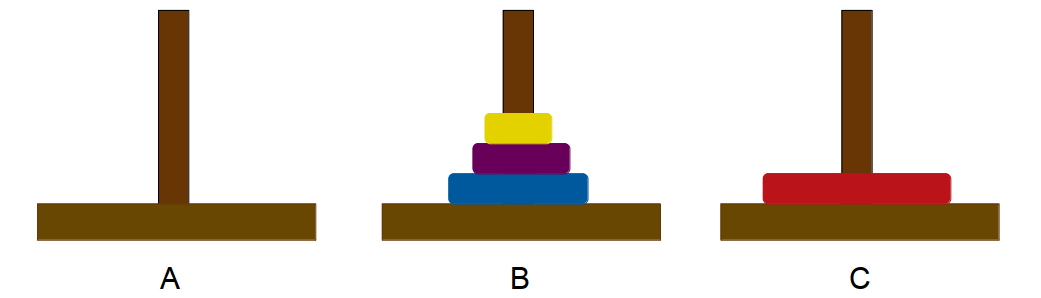
  • 步骤三：再用某种方法将 3 个圆盘从 B 柱移动到 C 柱

状态3

那么怎样来写递归关系式呢？我们看到，要解决 n 阶汉诺塔的问题，我们先要解决两个 n - 1 阶同样的问题，外加一个单次移动。所以我们的递归关系式应该这样写：

关系式

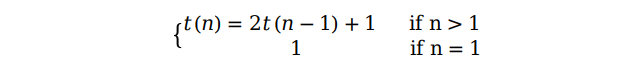
我们还是采用回代的方式解出这个关系式：

推导

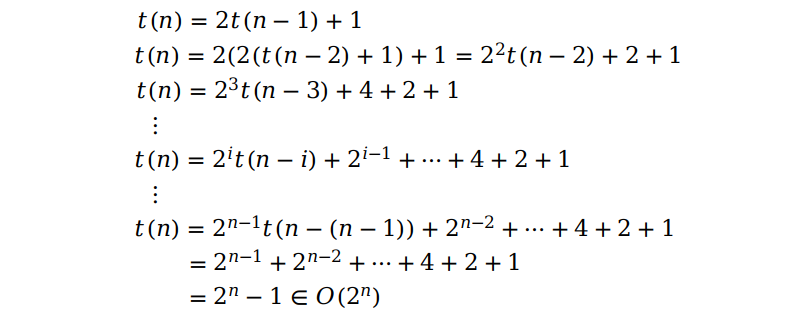
复杂度为 Θ(2n)，最后我们用代码来实现一下吧。

def hanoi(a, b, c, n):
    if n == 1:
        print("{} -> {}".format(a, c))
        return
    hanoi(a, c, b, n-1)  # c 柱为枢纽，将 a 柱中 n - 1 个圆盘移到 b 柱上
    hanoi(a, b, c, 1)  # 将待移动的圆盘数设为 1
    hanoi(b, a, c, n-1)  # a 柱为枢纽，将 b 柱中 n - 1 个圆盘移到 c 柱上

让我们试试 n = 3 时输出的结果：

>>> python hanoi.py
... a -> c
... a -> b
... c -> b
... a -> c
... b -> a
... b -> c
... a -> c

→ 本节全部代码 ←