最好,最坏和平均情况
一个算法的效率并不是一成不变的,在不同的情况下它会有不同的表现。先来看看一个生活中的场景,假设买彩票中奖的概率是1 / 10,000,那么在最好,最坏和平均的情况下需要买几注彩票才能够中奖呢?显然,如果你的运气够好,第一注你就直接中了,这是最好的情况;相反,如果你的手气够差,你买的彩票永远都中不了奖,这是最坏的情况;平均来讲,你需要买最少 10,000 注才能够中奖,其实就是这里的数学期望。

这里的类比并不是想说明算法跟概率学有任何的关系,只是想告诉大家,一个算法的复杂度是有最好,最坏和平均之分的,它取决于一个或一类问题的实例(instance)。这里的实例可以这样来理解:如果排序是我们要解决的问题,也就是对任意无序数组的有序化,那么一个实例就指的是一个具体的数组,比如 [3, 1, 2, 5, 4] 或 [1, 2, 3, 4, 5]。
我们可以看到,数组 [1, 2, 3, 4, 5] 已经有序了,所以不需要再额外执行任何操作。对于有些排序算法来讲就可以利用这一点特点,减少执行的次数,让算法更有“远见”。像这样能使一个算法执行次数最少的情况我们把它叫做最好情况(best case)。相反,使一个算法执行次数最多的情况叫做最坏情况(worst case)。最后剩下的平均情况(average case)指的是一般情况下算法的复杂度,它并不是等于(最好情况 + 最坏情况)/ 2 这么简单,而是要把所有的 instance 考虑在内,计算复杂度,然后再求一个平均值,后面的例子我会详细说明这个问题。
顺序查找
如果我们要查找数组里的某个元素,首先想到的办法就是通过顺序查找的方式进行,也就是从数组的第一个元素开始,从左往右依次查找。实现代码如下:
def find(array, element):
length = len(array)
for i in range(length):
if array[i] == element:
return i
return -1
我们用一个for循环遍历整个数组,如果找到了element就返回相应的索引值,否则返回-1。判断这一条件是否成立的语句显然是if array[i] == element,同时它也是被执行的最多的语句,我们将算法中执行次数最多,耗时最长的操作叫做基本操作(basic operation)。一般这种操作出现在最内层的循环,或者出现在有递归的地方。
然后,我们来分析一下在最好和最坏情况下的时间复杂度。首先,最好的情况是循环的第一个元素就是我们要找的,比如我们要从数组 [3, 1, 2, 5, 4] 中找元素 3,那么时间复杂度显然就为 Θ(1);最坏的情况是最后一个元素才是我们要找的或者查找失败,比如在这样的数组 [1, 2, 4, 5, 3] 中查找 3 则需要执行 5 次基本操作。假设数组的长度为 n,则需要 n 次,所以复杂度为 Θ(n)。
最后我们来说一说平均复杂度,如果我们考虑了所有的情况,即查找的元素element在数组array的每一个位置都会出现,且它们出现的概率是相等的,那么我们可以通过下面这样一个式子来计算:
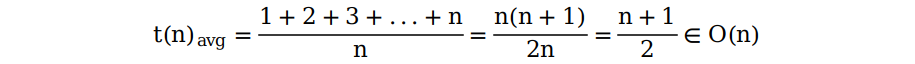
其中分子项为每一种情况需要查找的次数,最后得到的复杂度也为 Θ(n),表明了在一般情况下该算法的时间复杂度仍为线性复杂度。
矩阵乘法
让我们再来看一个例子,相信学过线性代数的小伙伴对矩阵的乘法应该不陌生,假设有两个矩阵 A ∈ Rm×n 和 B ∈ Rn×p,最后得到的矩阵 C ∈ Rm×p> 中每一项都是 A 中每一行的 n 个元素和 B 中每一列的 n 个元素依次相乘的和。下面是一个动图的演示(摘自3Blue1Brown里的视频):
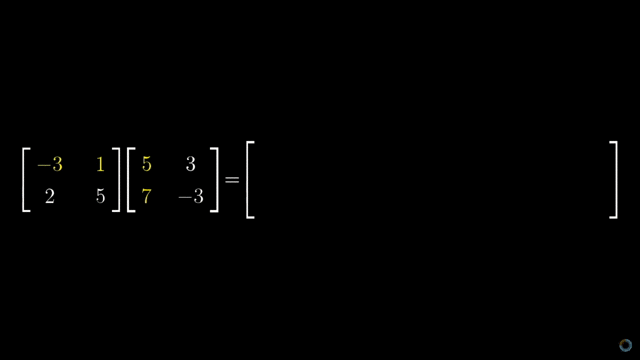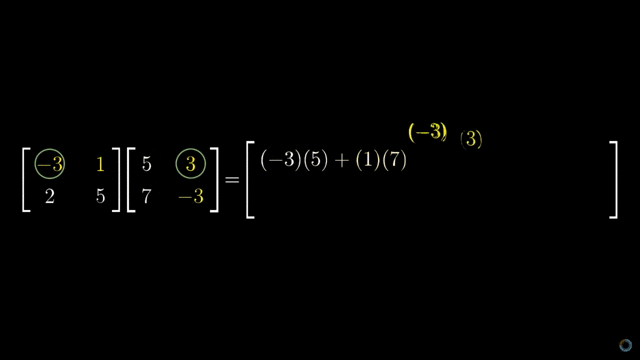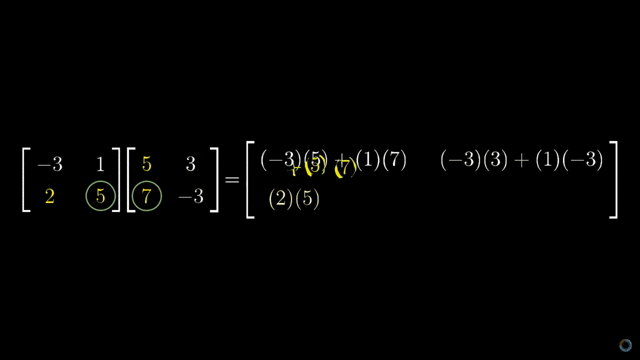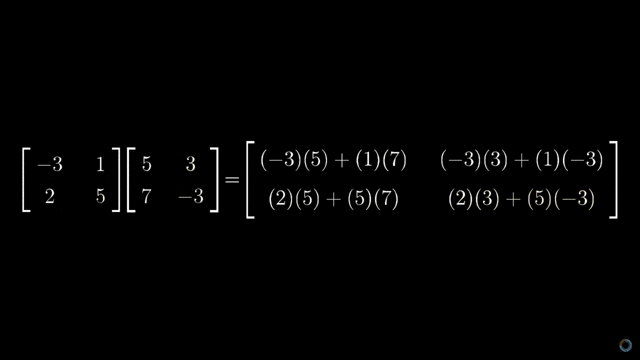
把它翻译成代码:
def matmul(A, B):
n = len(A)
C = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
for j in range(n):
for k in range(n):
C[i][j] = C[i][j] + A[i][k] * B[k][j]
return C
这里为了更好地表示问题的规模 n,两个矩阵都采用了方阵的形式。很显然,C[i][j] + A[i][k] ∗ B[k][j]位于循环的最内侧,所以作为这里的基本操作。更严格地来说,由于在计算机里做乘法所耗费的时间比做加法要多,所以 A[i][k] ∗ B[k][j] 才是真正的基本操作。
分析完了基本操作,下面就来计算复杂度了。因为这里不管什么样的矩阵,它们执行的基本操作都是一样的,所以就不存在最好,最坏和平均情况的讨论了。于是根据代码中三重循环我们可以得到下面的式子:
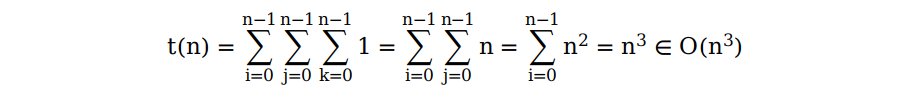
最后复杂度为 Θ(n3)。是不是很简单呢?类似的例子还有很多,这里就不一一列举了。
→ 本节全部代码 ←