解决的问题
在图的遍历那一节的最后我们提到,不管是深度优先遍历还是广度优先遍历,本质上都是对图中的每一个节点执行一次遍历算法,来达到遍历整个图的目的。本节会讲到的暴力搜索(exhaustive search)就是专门为了解决这类问题而产生的。它解决的问题以组合问题这类复杂的问题为主,下面我们一起来看两个经典的例子。
背包问题
背包问题是一道典型的组合问题,我们可以这样来描述它:给你一些物品,这些物品都有它对应的重量 wi 和价格 vi ,并且每个物品只能选择一次。现在有一个最多能装 W 重量的背包,你要怎样来组合这些物品来使得背包里物品的价格最大。
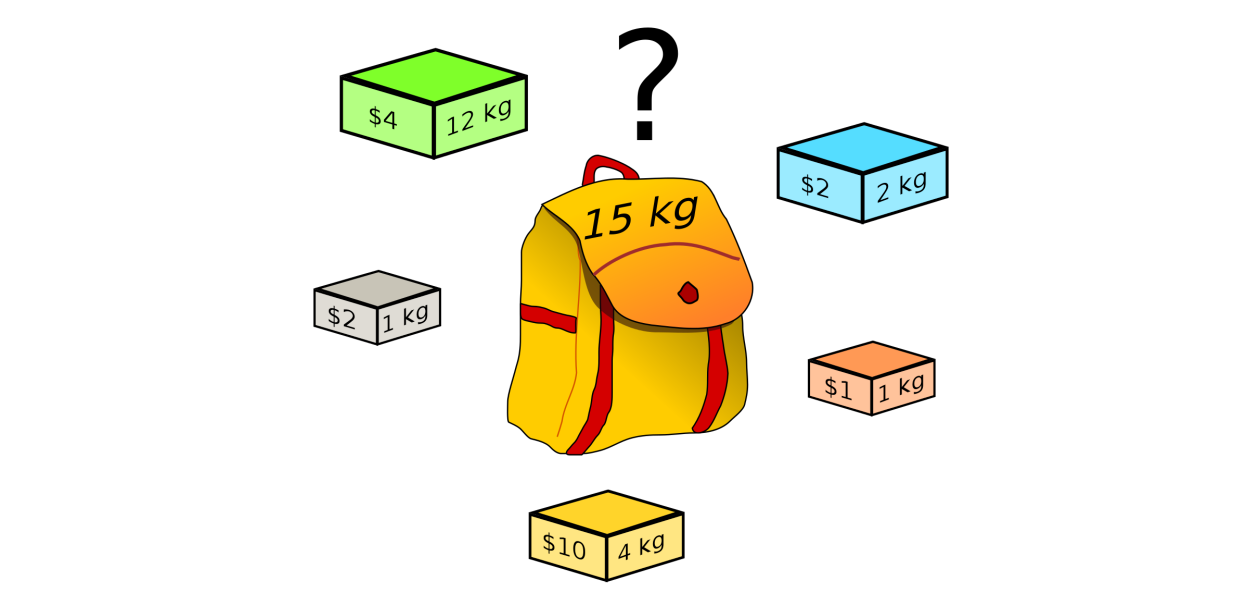
暴力搜索的方式就是将这个问题的全部组合一一列举出来,即穷举集合 {w1, w2, …, wi, …, wn } 中所有的子集,然后判断重量是否超过了背包上限,如果没有,就分别计算它们的价格,最后选出最高价格的组合。
下面来举一个具体的例子。假设这里的 W = 10,w1 = 7, v1 = 42; w2 = 3, v2 = 12; w3 = 4, v3 = 40; w4 = 5, v4 = 25。那么根据我们的实例,列举出所有的情况:
| 子集 | 总重量 | 总价格 |
|---|---|---|
| ∅ | 0 | 0 |
| {w1} | 7 | 42 |
| {w2} | 3 | 12 |
| {w3} | 4 | 40 |
| {w4} | 5 | 25 |
| {w1, w2} | 10 | 54 |
| {w1, w3} | 11 | 不符合要求 |
| {w1, w4} | 12 | 不符合要求 |
| {w2, w3} | 7 | 52 |
| {w2, w4} | 8 | 37 |
| {w3, w4} | 9 | 65 |
| {w1, w2, w3} | 14 | 不符合要求 |
| {w1, w2, w4} | 15 | 不符合要求 |
| {w1, w3, w4} | 16 | 不符合要求 |
| {w2, w3, w4} | 12 | 不符合要求 |
| {w1, w2, w3, w4} | 19 | 不符合要求 |
总共有 24 = 16 种情况,如果我们取出那些符合要求的情况,选择价格最大的一种,问题就解决了,最后的结果为:{w3, w4} 这种组合,其价格为 65。
如果要写成代码,我们首先要构建一个从集合 {w1, w2, w3, w4} 中产生超集(集合的全部子集所构成的集合)的函数 power_set_gen。
def power_set_gen(w):
p_set = [set()]
for item in w:
temp_set = []
for subset in p_set:
subset = subset | {item} # 将新元素加入到原有的子集中
temp_set.append(subset)
p_set.extend(temp_set)
return p_set
写好构建好超集的函数后,我们就可以在主函数knapsack函数里面枚举所有的情况啦。
def knapsack(w_v, p_set, W):
w_combination = None; max_value = 0 # 分别用来记录最优情况的组合和最大值
for instance in p_set:
weight, value = 0, 0 # 累加器
for item in instance:
weight += item; value += w_v[item]
if weight <= W and value > max_value:
w_combination = instance
max_value = value
return w_combination, max_value
最后求得的结果和我们分析的一样。
>>> python knapsack.py
>>> 最佳组合为物品 3 和物品 4,其价格为 65。
关于复杂度的问题,只要你知道一个含有 n 个元素的集合的子集数为 2n,就能轻松得出复杂度为 Θ(2n)了。
分配问题
分配问题是另一道经典的组合问题,问题的描述为一家公司有 n 名员工,现在有 n 件任务需要分配给这些员工,一件任务只能分配给一名员工,每名员工完成每件任务都有对应的时间,现在要我们来分配这些任务,最后使总时间最短。

来看一个具体的例子,我们将每名员工完成每件任务所需要的时间用一张表格表示出来:
| 任务 1 | 任务 2 | 任务 3 | 任务 4 | |
|---|---|---|---|---|
| 员工 1 | 9 | 2 | 7 | 8 |
| 员工 2 | 6 | 4 | 3 | 7 |
| 员工 3 | 5 | 8 | 1 | 8 |
| 员工 4 | 7 | 6 | 9 | 4 |
下面我们看看具体该如何来分配。任务 1 可以分配给 4 名员工中的任意一位,当任务 1 分配给一名员工之后,任务 2 就只能分配给剩下的 3 名员工中的一位了,然后任务 3 分配给剩下两名中的一位,最后任务 4 交给最后未分配的员工。因此根据前面的描述,我们枚举出所有的情况,将最优情况用“暴力”的手段搜索出来,于是我们写出相应的代码。
首先需要有一个生成全排列的函数,来指定每个员工对应的任务序号。
def perm_gen(source):
permutation = [[source[0]]]
for i in range(1, len(source)):
temp = []
for p in permutation:
for j in range(len(p), -1, -1):
p.insert(j, source[i])
temp.append(p.copy())
p.pop(j)
permutation = temp.copy()
return permutation
让我们来试一试123的全排列。
>>> print(perm_gen([1, 2, 3]))
>>> [[1, 2, 3], [1, 3, 2], [3, 1, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1]]
然后写出我们的主函数:
def assignment_bf(perm, table):
combination = None; min_cost = np.inf # 分别用来记录最有情况的组合和最小值
for i in range(len(perm)):
temp_cost = 0 # 累加器
for j, k in enumerate(perm[i]):
temp_cost += table[j][k-1]
if temp_cost < min_cost:
combination = perm[i]
min_cost = temp_cost
return combination, min_cost
最后输出结果:
>>> python assignment.py
>>> 最佳分配方案为:
>>> 员工 1 做任务 2,员工 2 做任务 1,员工 3 做任务 3,员工 1 做任务 4。
>>> 最短时间为 13
如果我们把上面问题的规模扩大到 n,按照上面的方式,我们可以列举出的情况有 n! 种,所以用暴力搜索的方式解决分配问题的复杂度自然就为 Θ(n!) 了。
我们可以看到,用暴力搜索的方式解决这两类问题,复杂度分别达到了指数级和阶乘级。千万别小看指数和阶乘,要知道,就算当问题的规模很小(n = 20)时,计算机都不能在有限的时间内将它们计算出来,尤其是阶乘级的复杂度,因为 20! 就已经达到了 2.4 × 1018 这么大,更何况在现实中的问题规模都是 106 起步的。所以,用暴力搜索解决组合问题显然是不切实际的。后面的动态规划和分支限界法会给出更为优质的算法来解决这类问题。
→ 本节全部代码 ←