Hexo |

暴力求解

从这一章开始，我们就要用算法去解决具体的问题了。别忘了前面我们提到过，我们并没有按照类别将这些算法问题分类（排序，搜索，等），而是按照不同的解决方法来划分的。在我们还没有了解那些高(ling)深(ren)莫(tou)测(teng)的算法之前，我们先来学习一种最简单也是最容易理解的解决方式：暴力求解（brute-force）。

step

从字面上理解暴力求解就是利用计算机快速计算的优势，用蛮力的方法解决一切问题，也就是根据问题描述直接写出相应的算法，从而忽略我们观察和分析问题的过程。举两个例子，前面提到的扔鸡蛋的问题，假如你从第一层开始一层一层地试，直到试出在哪一层鸡蛋刚好会碎，这种方法就是最简单，最直接的方法，也是你一看问题便能想到的办法。另一个例子就是假设让你猜一个 1-100 之间的整数，每次猜完之后会告诉你大了还是小了，你可能会想到从 1 开始一个一个递增地往上猜，但这样显然不是最高效的方法，聪明的你肯定会从两个数的中间开始猜，这样会大大减小猜的次数，效率明显比一个一个才要高。像这样的方法我们在后面还会再次提及。

从两个简单的例子我们似乎可以提前得出结论：暴力求解的效率一定不会很高，但我们可以很方便的写出代码。因此，对于一些规模很小的问题我们可以采用这种方式，但对于规模较大的问题，暴力求解需要计算的次数可能随着问题的规模呈现指数级的增长，那时候我们计算机的 CPU 可能就吃不消了。

sick

冒泡排序

下面我们就从两种最简单的排序算法开始介绍。首先是冒泡排序（bubble sort），当你一听到这个名字的时候，你就可能认为它跟冒泡泡有一定关系。哈哈，事实上的确如此，我们可以先从一个动画（来源于网络）直观地感受一下：

可以看到的是，每次循环，左侧较大的元素会向右“浮动”到相应的位置，如果把它旋转 90 度，这些数就好像在“冒泡”了。实际上，冒泡排序做的事情很简单，i从 0 开始，每次处理的数组长度为len(array)-i，在每次的待处理的数组中，相邻的元素之间两两比较，如果乱序就交换位置，一直重复前面的过程直到数组有序。因为在每次循环中，那些较大的数总是要跟较小的数做交换，所以在直观上就好像这些较大的数在向一个方向“浮动”了。

冒泡排序的实现非常简单，几行代码就能够搞定：

def bubble_sort(array):
    n = len(array)
    for i in range(n-1):
        for j in range(n-1-i):
            if array[j] > array[j+1]:
                array[j], array[j+1] = array[j+1], array[j]
    return array

其中n为数组的长度。那冒泡排序的效率如何呢？根据我们前面所学的复杂度分析的内容，我们可以得到并推导出下面的式子：

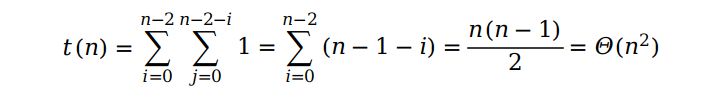
最后我们得到冒泡排序的复杂度为 Θ(n²)。

选择排序

选择排序（selection sort）是暴力求解来解决排序问题的第二种方法，同样它也非常好理解，让我们先从一个动画（来源于网络）演示中来一探究竟吧。

从动画中可以看到，每次循环都会从右侧未排序的序列中选择一个最小的数，与未排序的序列中的第一个元素交换，然后反复这个过程，直到循环结束。

选择排序用 Python 实现也很容易，也只需要几行代码：

def selection_sort(array):
    n = len(array)
    for i in range(n-1):
        min = i
        for j in range(i+1, n):
            if array[min] > array[j]:
                min = j
            array[i], array[min] = array[min], array[i]
    return array

因为要暂存那些最小值的索引值，所以这里用到了一个变量min。最后来分析一下选择排序的复杂度，跟冒泡排序一样，根据循环结构找出 basic operation(if array[min] > array[i])，在统计执行的次数即可，因而我们最后推导出选择排序的时间复杂度也为 Θ(n²)

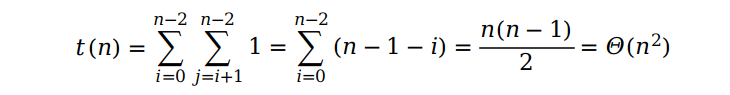
从时间复杂度我们可以看出，这两种排序算法的效率都不高。为了间接的证明这个结论，我在这一节的完整代码里用到了每次排序所需要的比较次数和排序时间这两个指标来间接反映这一结论。后面我们还会接触到一些更为高效的算法，大家也可以通过这两个指标来判断一个排序算法效率如何。

下面是运行后的结果：

>>> python bubble.py
... 平均比较次数: 49995000
... 平均运行时间: 9.3161 s

>>> python selection.py
... 平均比较次数: 49995000
... 平均运行时间: 4.7869 s

稳定性

下面来介绍一下排序算法的一个很重要的性质：稳定性（stability）。一个排序算法的稳定性在于原来具有相同大小的元素在排序后其相对顺序仍保持不变。

举个简单的例子，如下图所示，排序前数组中红色的 4 位于蓝色的 4 的前面，如果排序后红色的 4 还在蓝色的 4 的前面，则该排序算法是稳定的，反之则不稳定。

稳定性

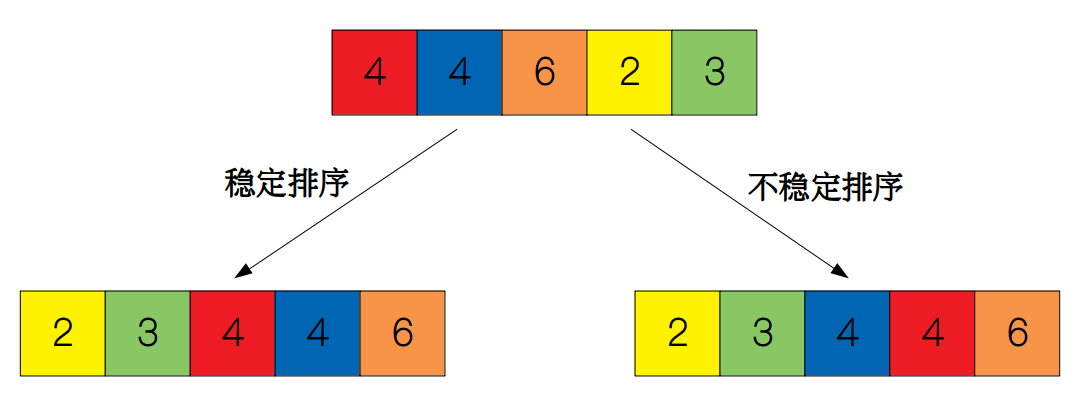
我们先来看看冒泡排序的稳定性如何，我们知道，冒泡排序是数组的相邻元素进行大小比较，每次比较元素只能跟相邻的元素发生交换，所以相同大小的元素的相对顺序不可能发生变化，所以冒泡排序是一个稳定的排序算法。

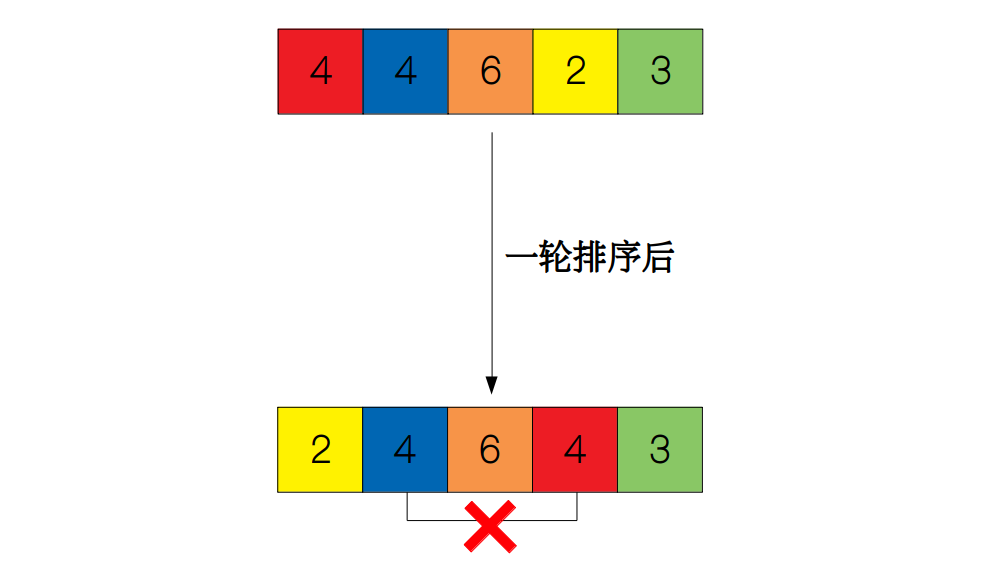
再来说一说选择排序，我们不太能从算法本身分析出稳定性，所以这里我们直接举出选择排序不稳定的例子，下图的数组选出最小元素 2 并与第一个元素 4 交换顺序后，红色的 4 的和蓝色的 4 的顺序发生了变化，所以选择排序是一个不稳定的排序算法。

稳定性

→ 本节全部代码 ←