概述
前面讲到了很多关于数据结构的概念,后面的内容就要用这些数据结构和算法来解决具体的问题了。那么首先我们是不是应该对这些问题归一个类呢?废话不多说,先列举出来,主要分为五大类:
- 排序问题
- 搜索问题
- 图的问题
- 几何问题
- 组合问题
排序问题
排序问题是计算机科学里最基础,也是最重要的问题,很多情况下直接决定了你设计的程序的效率,因为很多程序都会用到排序。在实际生活中排序也是用处多多。一个最简单的例子就是国外大学的招生办将申请者的 GPA 全部导入到 Excel 中,然后从高到低依次排序来筛选出他们想要的学生。
排序所要实现的功能也很简单,我们的输入可以是一串无序的数字或者字母,输出就是从大到小或从小到大排列的有序数组,像这样:
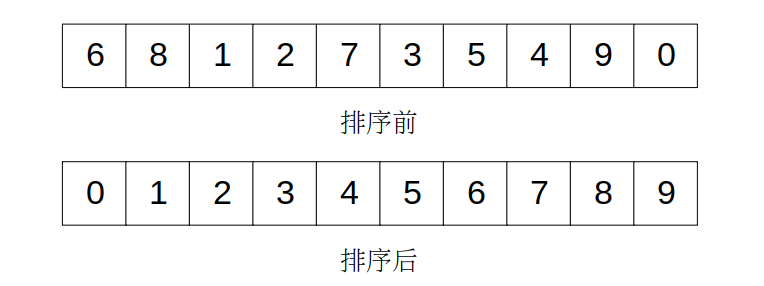
搜索问题
搜索也是我们无时不刻都会用到的一个功能。Google 和百度的服务器每天都要从互联网上爬取海量的数据,然后将它们放在搜索树中以便于用户的查找。试想,如果这个搜索的效率很低很低,要几十秒甚至是几分钟才搜索出结果,那这两家公司可能也不会有今天的成就了吧。
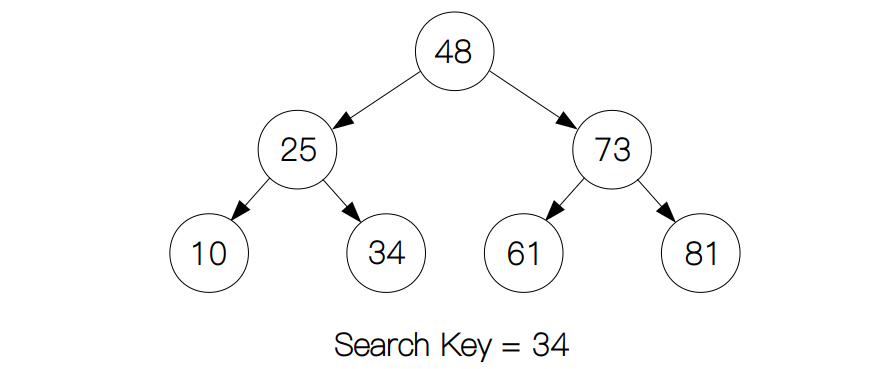
所以这就是我们要讨论的第二个问题:搜索问题。它可以再分为两个类,一个是单一键的搜索,例如下面这颗二叉树(binary tree),我们要搜索键为 34 的节点是否存在:
第二个问题是关于字符串匹配(string matching)的。假设我们有一段英文:“A fall into a pit, a gain in your wit.”,现在要从里面查找 pit 这个单词以及它所处的位置。跟第一种不同的是,我们要查找的不再是一个单一的键而是一个字符串。这样就和我们从网页或电子书里搜索一段话一样了。
图的问题
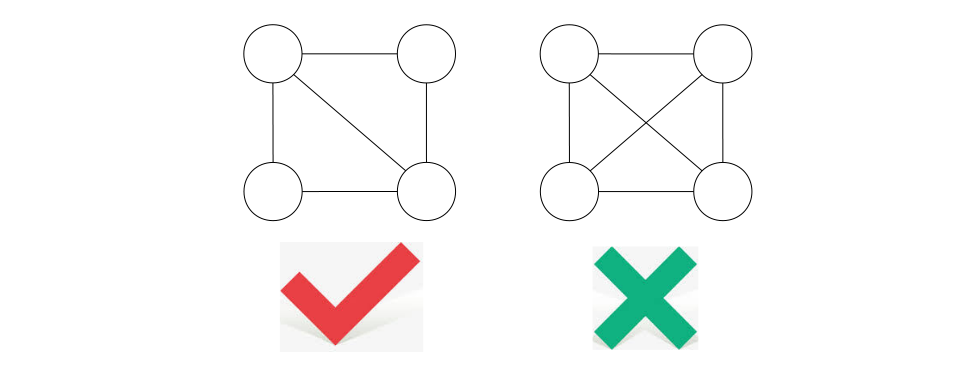
图的问题可谓是应用面最广的问题类型之一了。当我们开车迷路时,我们的手机里的高德地图总是给我们规划好距离最短的路线,或是耗时最短的路线,引领着我们到家。再就是小的时候玩过的一笔画游戏,其抽象成图的问题就为:给定一些图的节点和边集合 V, E,总是存在一条路径包含了所有的边,且每条边只能被访问一次。下图就分别列举出了存在和不存在的情况。这些通通都要用到图的算法来解决。
几何问题
几何问题当然就是讨论关于点、线、面的问题啦。这里有一个最经典的问题:邮局选址问题。问题的描述是一条笔直的马路两侧分布着一些村庄,现在要在这些村庄之间修建一个邮局,使得所有村庄离这个邮局的距离之和最短。后面我们还会讨论最近点对问题(closest-pair problem)和凸包问题(convex-hull problem)。

组合问题
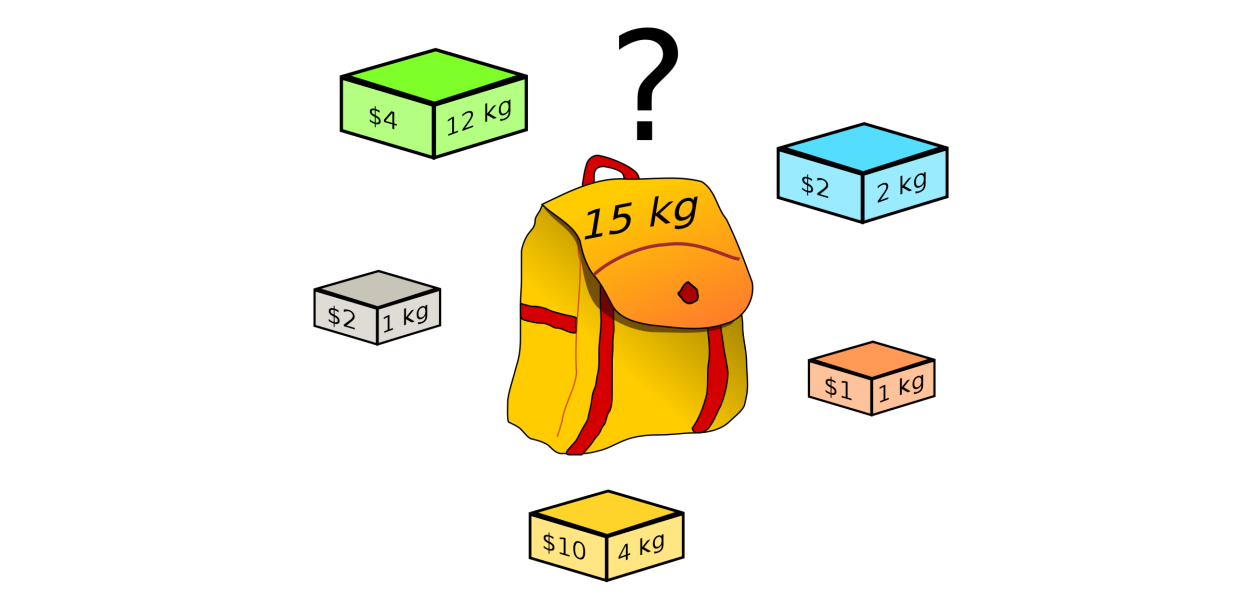
前面提到的一笔画问题不仅是关于图的问题,同样它也是一个组合问题,这样的问题试图从排列组合中找到答案。我们知道,排列组合问题的规模一般都非常大,所以组合问题也是算法里面最耗时,最难解决的一类问题。后面我们还会讨论背包问题(knapsack problem),分配问题(assignment problem)等一系列组合问题。