概念
如果说程序员是用代码编织这个世界的一群人,那么数据结构(data structure)就是编织所用到的各种工具了,它将计算机中各种各样的数据组织在一起。而我们的算法就是利用这些现有的工具将它们拼接成风格、功能各不相同的程序了。简单来说:算法 + 数据结构 = 程序。这一节就让我们来了解一些基本的数据结构吧。
数组与链表
我们从最简单的一维数据结构开始。数组大家应该都不陌生,它是将一组相同数据类型的数据存储在一起的数据结构。

一个数据结构都有它对应的操作(方法),这里我们分析一下最基本的三大操作:查找、插入和删除。
拿上面的图为例,因为数组中每一个元素(element)都有自己的一个下标,称为索引(index),它们被存储在计算机的 RAM 中,所以查找的速度非常快。一般查找的时间不随数组长度而增加。
插入和删除就要稍微麻烦一些。因为数组占用的是计算机内存的连续地址空间,所以在插入一个新元素时,所有在它后面的元素都要向后移动一个单位,为新元素“腾出”空位。同理,为了保持数组的连续性,删除一个元素后,所有在它后面的元素也要向前移动一个单位,以此来“填充”空位。
以这里的数组为例,如果我们要删除 index = 5 的元素,那么在它后面的 15, 34 和 80 都要向前移动一个单位,如下图中所示。

让我们用代码来实现一下这几个过程。
# 查找
def search(array, element):
length = len(array)
for i in range(length):
if array[i] == element:
return i
return -1
# 插入
def insert(array, idx, element):
new_array = array.copy() + [None] # 复制原数组到一个新数组
length = len(new_array); i = length - 1
# 所有idx之后的元素向右移动一个单位
while i > idx:
new_array[i] = new_array[i-1]
i -= 1
new_array[idx] = element
return new_array
# 删除
def remove(array, element):
length = len(array)
idx = search(array, element) # 找到对应索引
if idx != -1:
# 如果查找成功,所有在idx之前的元素向左移动一个单位
while idx < length - 1:
array[idx] = array[idx+1]
idx += 1
array = array[: -1]
return array
再来说一说链表。与数组采取的顺序存储方式不同,链表中所有的元素的存储地址都是分散的,虽然是分散的,但元素之间靠一条链条(指针)联系在一起。所以我们把链表中每一个存储单元称为一个节点(node),在每个节点里有两个域:一个用来存储数据,一个是指针用来指向下一个节点,像这样:
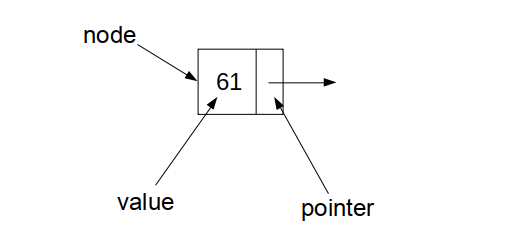
在 Python 中我们用一个类来表示:
class Node(object):
def __init__ (self, value, next):
self.value = value
self.next = None
如果将它们串联在一起,将会是这样:

其中的header指的是头结点,它一般记录第一个节点的地址和链表的长度,我们在查找的时候就是从头结点开始,逐个访问节点,如果查找成功就返回该节点;如果失败就返回None。
class Linked_List(object):
def __init__ (self):
self.length = 0
self.header = None
def search(self, value):
p = self.header # 获取第一个节点
while p != None:
if p.value == value:
return p
p = p.next
return None
和数组相比,链表的插入和删除就非常的简单,只需要改变一下指针即可。下面还是以插入元素 61 为例:
首先需要新建一个节点p。
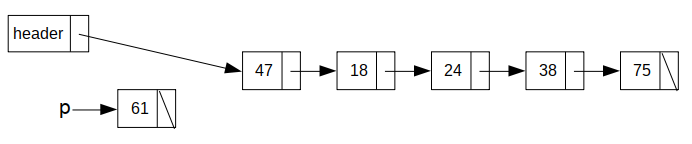
然后,p的指针指向头结点所指的节点
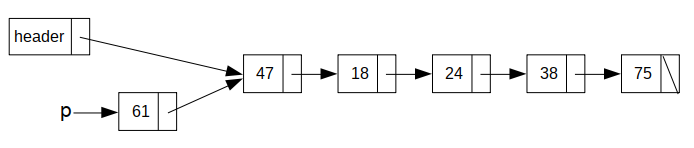
最后,改变头结点的指针,使其指向p,同时更新链表的长度length。
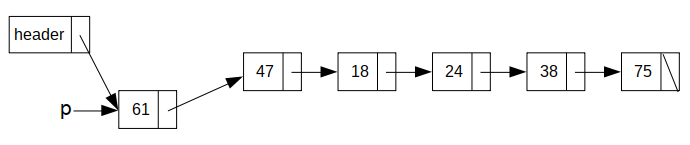
插入和删除的实现:
class Linked_List(object):
def __init__ (self):
self.length = 0
self.header = None
def insert(self, value):
# 新建一个节点
p = Node(value)
p.next = self.header
self.header = p
self.length += 1
def remove(self):
p = self.header # 获取第一个节点
if p is not None:
self.header = p.next
self.length -= 1
del p # 删除节点 p
ADT
抽象数据类型(Abstract Data Type, 简称ADT)是数据结构中非常重要的一个部分。用最简单的理解方式就是:不仅限于编程语言中已经实现的一些数据类型,例如 Python 中 list,set,tuple,dictionary 等等。我们可以进一步的定义出属于我们自己数据结构,比如说增删只能在一侧进行,具有层状、环状的结构等等,下面就列举了几个常见的抽象数据类型。
栈
栈(stack)就是前面提到的只能在一侧进行元素的增加和删除的数据结构,这种过程分别叫做入栈(push)和出栈(pop)。生活中最简单的类比就是叠盘子,新洗好的盘子总是放在最上面,而拿走的时候总是从最上面一个拿走。这种后进先出(last in, first out)的方式就体现了这种思想。

队列
和栈相反,队列(queue)是遵循先进先出(first in, first out)的方式实现元素的增减,其过程分别叫做入队(enqueue)和出队(dequeue)。生活中的例子就是去超市收银台排队的时候,排到队伍后面的人要先等前面的人都结完账了自己才能结账,所以这就是先进先出啦。

因为和前面的数组和链表有相似性,所以这里就不再用 Python 的代码做演示了,你可以去我的 GitHub 主页查看本节的完整代码。
树
与前面的数据结构不同,树(tree)是典型的层状数据结构。直观上来看,它就像倒挂着的一颗树,每一个节点连接着多个子节点。这里为了方便,我们只讨论用得最多的二叉树(binary tree),也就是每一个节点最多只有两个子节点的情况。
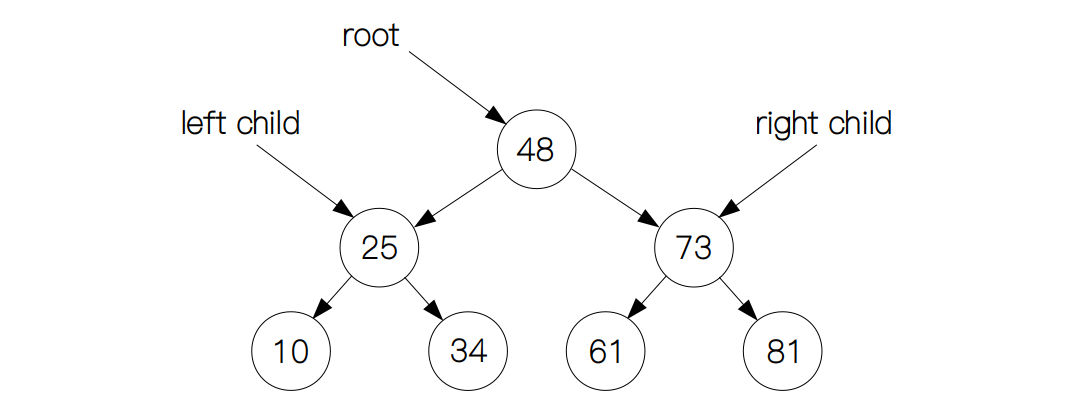
下面来简单介绍一下二叉树的性质,和所有树状结构一样,二叉树在非空的情况下一定有一个根节点(root node),如图中的节点 48。它的两个子节点我们分别把它们叫做该节点的左孩子(left child)和右孩子(right child),而对于那些没有孩子的节点,我们把它叫做叶子节点(leaf node)。前面只是针对节点的讨论,而对于树本身,我们要了解的是满二叉树和完全二叉树。
满二叉树是指每一个节点孩子的个数只能为 0 或 2 ,如下图所示,左边是一颗满二叉树,但右边由于节点 81 只有一个孩子,所以就不是满二叉树。
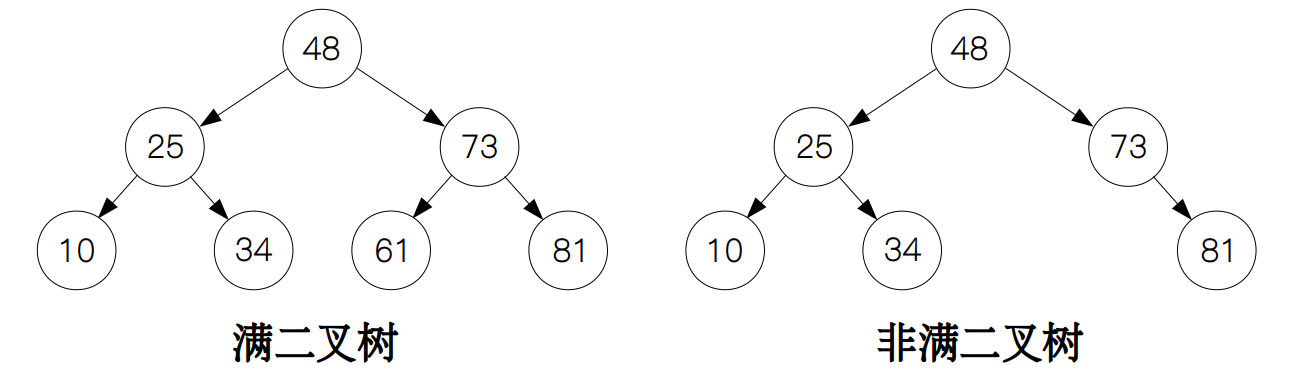
再来看看完全二叉树,它的性质是除了最后一层的节点没有排满以外,其他层的节点均已排满,并且最后一层节点都是从左往右依次排列。下图的两个例子分别代表了完全二叉树和非完全二叉树。后面的堆也会用到这种性质。
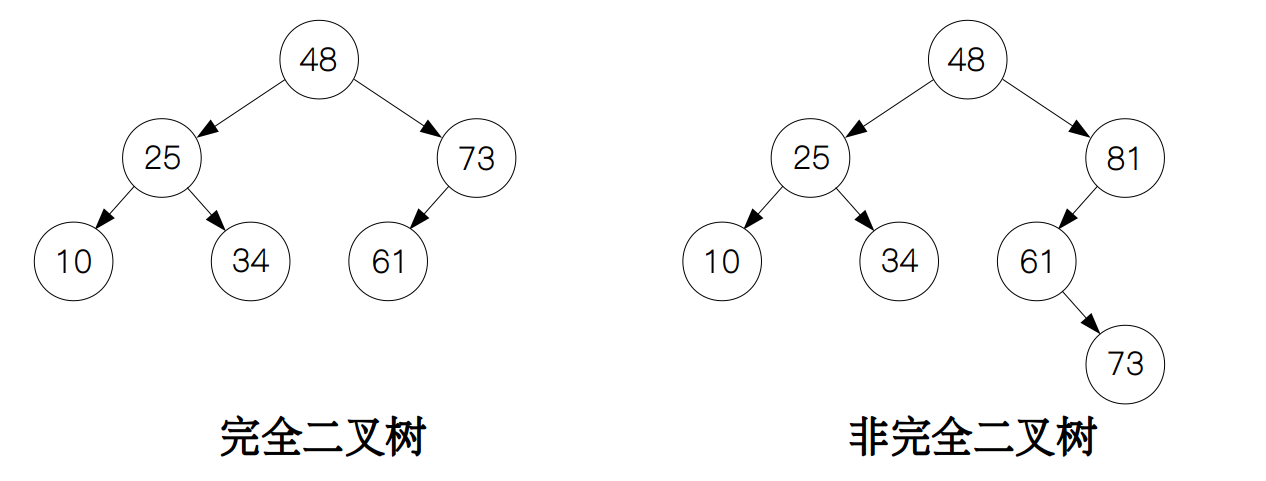
在 Python 中我们可以用一个类来表示树的节点:
class Node(object):
def __init__ (self, value):
self.value = value
self.left = None # 左孩子
self.right = None # 右孩子
图
图(graph)是 ADT 中用到的最多的结构,生活中的方方面面都会用到图。例如,高德地图就是把所有城市,所有道路通通抽象成了图这种数据结构来帮助我们导航的。那我们就首先来了解一下图的基本结构。
图也是由一个一个的节点(vertex)组成的。但与树不同的是,图的节点之间相连的叫做边(edge),所以我们用 G = <V, E> 来表示一张图,其中的 V 表示由 vertex 构成的集合,而 E 则表示由 edge 构成的集合。
图可以分为好几种,如果一个节点到另一个节点是双向的我们把它叫做无向图(undirected graph),如果是单向的就叫有向图(undirected graph),下图中就分别代表了无向图和有向图。
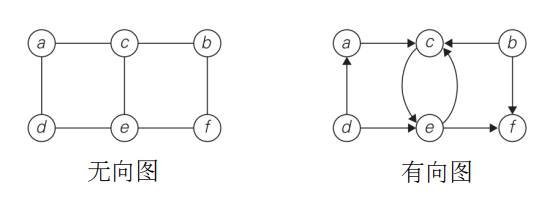
假如从一个节点到另一个节点是要付出“代价”的,就像从一个城市到另外一个城市需要用距离来度量一样,那么我们就可以在每一条边上把这种“代价”体现出来,称之为权重(weight),而构成这样的图当然就叫做有权图(weighted graph)了。
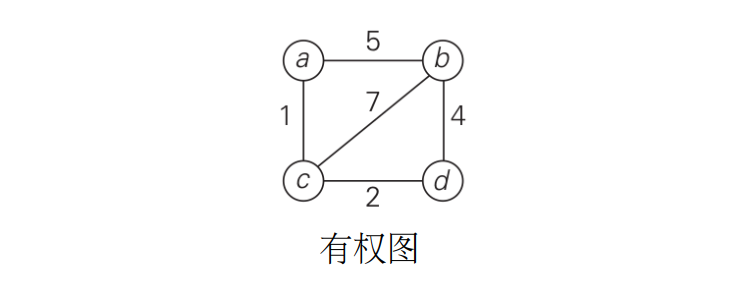
我们可以用两种数据结构来表示一张图,一种叫做邻接矩阵(adjacency matrix)和邻接表(adjacency list),后面的内容会详细讨论,先上图。
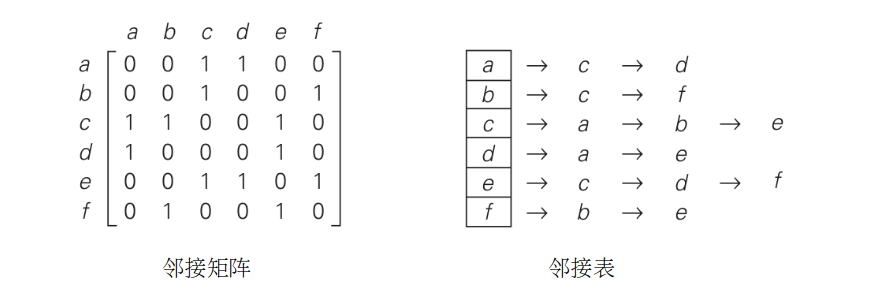
这样我们就完成所有基本数据结构的学习了,是不是对它们有了清晰的认识呢?
→ 本节全部代码 ←